浙江省历年(2019-2024)中考数学真题压轴解答题汇编(1)
试卷更新日期:2025-01-27 类型:二轮复习
一、综合题
-
1. 【问题背景】
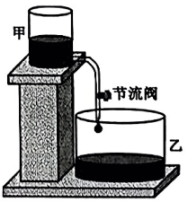
“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】
综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如下表:
流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务1 分别计算表中每隔10min水面高度观察值的变化量.
【建立模型】
小组讨论发现:“ , ”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2 利用时,;时,这两组数据求水面高度h与流水时间t的函数解析式.
【反思优化】
经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差.小组决定优化函数解析式,减少偏差.通过查阅资料后知道:t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和 , 记为w;w越小,偏差越小.
任务3 ⑴计算任务2得到的函数解析式的w值.
⑵请确定经过的一次函数解析式,使得w的值最小.
【设计刻度】
得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4 请你简要写出时间刻度的设计方案.
2. 如图1,点为矩形ABCD的对称中心, , 点为AD边上一点 , 连结EO并延长,交BC于点.四边形ABFE与关于EF所在直线成轴对称,线段交AD边于点。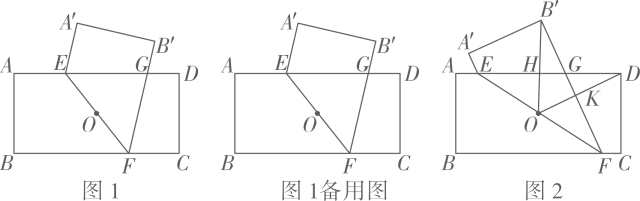 (1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.
(1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.①求证:(4-a)(4-b)=4.
②如图2,连结 , 分别交于点H,K.记四边形OKGH的面积为 , 的面积为.当时,求的值.
3. 小东在做九上课本123页习题:“1: 也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1: .”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.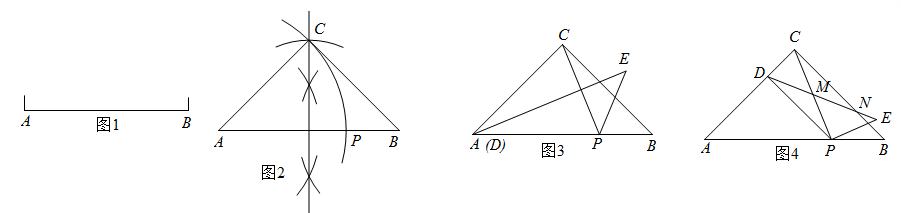 (1)、你赞同他的作法吗?请说明理由.(2)、小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
(1)、你赞同他的作法吗?请说明理由.(2)、小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
4. 如图1,锐角内接于 , D为的中点,连接并延长交于点E,连接 , 过C作的垂线交于点F,点G在上,连接 , 若平分且 .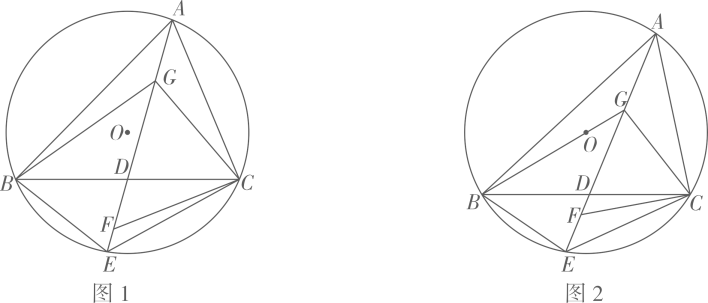 (1)、求的度数.(2)、①求证: .
(1)、求的度数.(2)、①求证: .②若 , 求的值,
(3)、如图2,当点O恰好在上且时,求的长.5. 在正方形ABCD中,点M是边AB的中点,点E在线段AM上(不与点A重合),点F在边BC上,且AE=2BF,连接EF,以EF为边在正方形ABCD内作正方形EFGH.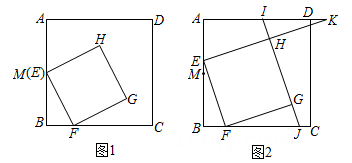 (1)、如图1.若AB=4,当点E与点M重合时,求正方形EFGH的面积(2)、如图2.已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.
(1)、如图1.若AB=4,当点E与点M重合时,求正方形EFGH的面积(2)、如图2.已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.①求证:EK=2EH;
②设∠AEK=α,△FGJ和四边形AEHI的面积分别为S1、S2 .
求证: =4sin2α-1.
6. 如图1,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位: m).如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 DEFG ,其水平宽度DE=3m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l 的距离OD为d(单位:m).

 (1)、若h=1.5,EF=0.5m;
(1)、若h=1.5,EF=0.5m;①求上边缘抛物线的函数解析式,并求喷出水的最大射程 OC;
②求下边缘抛物线与x 轴的正半轴交点B的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围;
(2)、若 EF=1m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.7. 如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H. (1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.
(1)、求证:AD∥HC;(2)、若=2,求tan∠FAG的值;(3)、连结BC交AD于点N.若⊙O的半径为5.下面三个问题,依次按照易、中、难排列,对应的分值为2分、3分、4分,请根据自己的认知水平,选择其中一道问题进行解答。
①若OF= , 求BC的长;
②若AH= , 求△ANB的局长:
③若HF·AB=88.求△BHC的面积.
8. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.9. 小贺在复习浙教版教材九上第81页第5题后,进行变式、探究与思考:如图1,的直径垂直弦AB于点E , 且 , .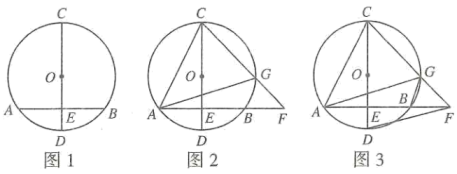 (1)、复习回顾:求的长.(2)、探究拓展:如图2,连接 , 点G是上一动点,连接 , 延长交的延长线于点F .
(1)、复习回顾:求的长.(2)、探究拓展:如图2,连接 , 点G是上一动点,连接 , 延长交的延长线于点F .①当点G是的中点时,求证:;
②设 , , 请写出y关于x的函数关系式,并说明理由;
③如图3,连接 , 当为等腰三角形时,请计算的长.
10. 如图,在矩形 ABCD中,AB=6,BC=8,动点 E从点A出发,沿边AD,DC向点C运动,A, D关于直线 BE的对称点分别为M,N,连结MN . (1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.11. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且.
(1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.11. 在平行四边形中(顶点按逆时针方向排列) , ∠为锐角,且. (1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.
(1)、如图1,求边上的高的长.(2)、是边上的一动点,点同时绕点按逆时针方向旋转得点.①如图2,当点落在射线上时,求的长.
②当当是直角三角形时,求的长.
12. 如图1,AB为半圆的直径,为BA延长线上一点,CD切半圆于点 , 交CD延长线于点 , 交半圆于点 , 已知.如图2,连结AF,P为线段AF上一点,过点作BC的平行线分别交CE,BE于点M,N,过点作于点.设. (1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.13. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且).
(1)、求CE的长和关于的函数表达式.(2)、当 , 且长度分别等于 , 的三条线段组成的三角形与相似时,求的值.(3)、延长交半圆于点 , 当时,求的长.13. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .14. 如图,在中,直径垂直弦于点 , 连接 , 作于点 , 交线段于点(不与点重合),连接 .
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .14. 如图,在中,直径垂直弦于点 , 连接 , 作于点 , 交线段于点(不与点重合),连接 . (1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.15. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.
(1)、若 , 求的长.(2)、求证: .(3)、若 , 猜想的度数,并证明你的结论.15. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.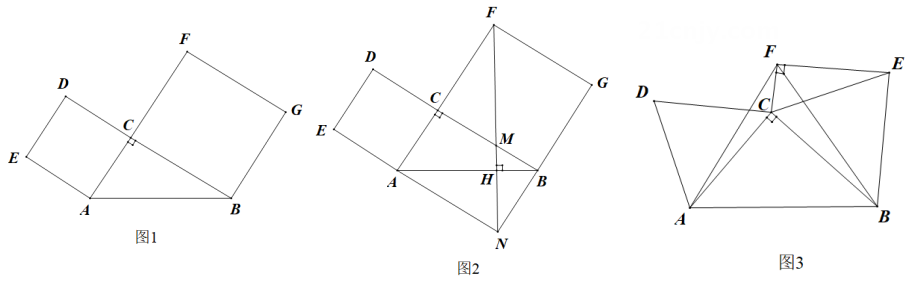 (1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .
(1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2-S1=2S.
(2)、如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1 , 等边三角形CBE的面积为S2 . 以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2-S1与S之间的等量关系,并说明理由.

