圆与一次函数—北师大版数学九（下）知识点训练

试卷更新日期：2025-01-12 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共24分）

1. 已知 $M (1, 2)$ ， $N (3, - 3)$ ， $P (x, y)$ 三点可以确定一个圆，则以下 $P$ 点坐标不满足要求的是（）

A、 $(3, 5)$ B、 $(- 3, 5)$ C、 $(- 1, 7)$ D、 $(1, - 3)$

查看试题解析
2. 在平面直角坐标系 $x O y$ 中，以 $P (0 ， - 1)$ 为圆心， $P O$ 为半径作圆，M为 $⊙ P$ 上一点，若点N的坐标为 $(a ， 2 a + 4)$ ，则线段 $M N$ 的最小值为（）

A、 $\sqrt{5} - 1$ B、 $2 \sqrt{5} + 1$ C、 $2 \sqrt{5} - 1$ D、 $\sqrt{5} + 1$

查看试题解析
3. 如图，直线 $y = - x + \sqrt{2}$ 与圆心在原点 $O$ ，半径为 $r$ 的圆有公共点，则 $r$ 的取值范围是（）

A、 $0 < r < 1$ B、 $0 < r \leq 1$ C、 $r \geq 1$ D、 $r \geq \sqrt{2}$

查看试题解析
4. 如图，在平面直角坐标系中，直线 $y = - \frac{\sqrt{3}}{3} x + \sqrt{3}$ 与坐标轴交于 $A$ ， $B$ 两点，圆心在 $x$ 轴上的 $⊙ P$ 经过 $A$ ， $B$ 两点，则 $⊙ P$ 的半径为（）

A、1 B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{3}$

查看试题解析
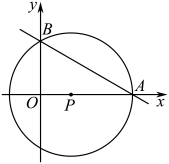5. 如图， $⊙ M$ 的圆心M在一次函数 $y = \frac{3}{5} x + 3$ 位于第一象限中的图象上， $⊙ M$ 与y轴交于C、D两点，若 $⊙ M$ 与x轴相切，且 $C D = 2 \sqrt{11}$ ，则 $⊙ M$ 半径是（）

A、 $\frac{27}{8}$ 或5 B、5或6 C、 $\frac{27}{8}$ 或6 D、5

查看试题解析
6. 如图，直线y＝ $\frac{\sqrt{3}}{3}$ x＋ $\sqrt{3}$ 与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 在平面直角坐标系 $x O y$ 中，点A在直线l上，以A为圆心， $O A$ 为半径的圆与y轴的另一个交点为E，给出如下定义：若线段 $O E$ ， $⊙ A$ 和直线l上分别存在点B，点C和点D，使得四边形 $A B C D$ 是矩形（点 $A ， B ， C ， D$ 顺时针排列），则称矩形 $A B C D$ 为直线l的“理想矩形”.例如，右图中的矩形 $A B C D$ 为直线l的“理想矩形”.若点 $A (3 ， 4)$ ，则直线 $y = k x + 1 (k \neq 0)$ 的“理想矩形”的面积为（）

A、12 B、 $3 \sqrt{14}$ C、 $4 \sqrt{2}$ D、 $3 \sqrt{2}$

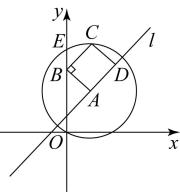查看试题解析
8. 如图5，在平面直角坐标系 $x O y$ 中，直线 $y = - x - 2$ 与x轴、y轴分别交于A、B两点，C、D是半径为1的 $⊙ O$ 上两动点，且 $C D = \sqrt{2}$ ， P为弦CD的中点．当C、D两点在圆上运动时， $△ P A B$ 面积的最大值是（）

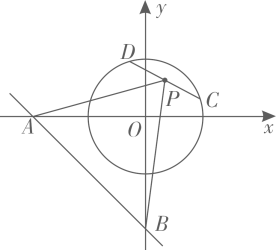A、8 B、6 C、4 D、3

查看试题解析

二、填空题（每题3分，共18分）

9. 在平面直角坐标系中， $O$ 为坐标原点，则直线 $y = x + \sqrt{2}$ 与以点 $O$ 为圆心，1为半径的圆的位置关系为

查看试题解析
10. 如图， $⊙ O$ 是以原点为圆心，半径为 $2$ 的圆，点 $P$ 是直线 $y = - x + 6$ 上的一点，过点 $P$ 作 $⊙ O$ 的一条切线 $P Q$ ， $Q$ 为切点，则 $S_{△ P Q O}$ 的最小值为．

查看试题解析
11. 如图，直线 $y = \sqrt{3} x$ ，点 $A_{1}$ 坐标为（1，0），过点 $A_{1}$ 作 $x$ 轴的垂线交直线于点 $B_{1}$ ，以原点 $O$ 为圆心， $O B_{1}$ 长为半径画弧交 $x$ 轴于点 $A_{2}$ ；再过点 $A_{2}$ 作 $x$ 轴的垂线交直线于点 $B_{2}$ ，以原点 $O$ 为圆心， $O B_{2}$ 长为半径画弧交 $x$ 轴于点 $A_{3}$ ；…，按此做法进行下去，点 $A_{2020}$ 的坐标为.

查看试题解析
12. 在直角坐标系xOy中，对于直线l：y＝kx+b，给出如下定义：若直线l与某个圆相交，则两个交点之间的距离称为直线l关于该圆的“圆截距”．如图，点M的坐标为（﹣1，0），若⊙M的半径为2，当k的取值在实数范围内变化时，直线l关于⊙M的“圆截距”的最小值为 $2 \sqrt{2}$ ，则b的值为．

查看试题解析
13. 如图，已知直线 $y = \frac{3}{4} x - 3$ 与x轴、y轴分别交于A、B两点，点P是以 $C (0 ， 1)$ 为圆心，1为半径的圆上一动点，连接 $P A ， P B$ ．则 $△ P A B$ 面积的最大值与最小值的差为．

查看试题解析
14. 如图，圆心都在x轴正半轴上的半圆O₁ ，半圆O₂ ， …，半圆On与直线y= $\frac{\sqrt{3}}{3}$ x相切．设半圆O₁ ，半圆O₂ ， …，半圆On的半径分别是r₁ ， r₂ ， ⋅⋅⋅，rn，则当r₁=1时，r₂₀₂₂= ．

查看试题解析

三、综合题（共5题，共58分）

15. 如图，在平面直角坐标系中，以原点О为圆心，3为半径作圆，直线y=mx-m+2与О相交于A，B两点，求弦AB的最小长度.

查看试题解析
16. 一次函数 $y = k x + b$ 的图象与 $x$ 轴的负半轴相交于点 $A$ .与 $y$ 轴的正半轴相交丁点 $B$ .且 $∠ A B O = 6 0^{°} ， △ O A B$ 的外接圆的圆心 $M$ 的横坐标为-3.求：

(1)、一次函数的表达式.

(2)、图中阴影部分的面积.

查看试题解析
17. 圆周角定理：圆周角的度数等于它所对的弧上的圆心角度数的一半．下面根据圆周角定理进行探究．

(1)、如图1， $A B$ 是 $⊙ O$ 的弦，点C是 $\overset{⌢}{A C B}$ 上一点，连接 $A C ， B C$ ，过点O作 $O D ⊥ A B$ 于点D，连接 $O A$ ， $∠ A C B = 5 0^{°}$ ，求 $∠ A O D$ 的大小．

(2)、在平面直角坐标系中，已知点 $A (2 ， 0)$ ， $B (6 ， 0)$ ．
（ⅰ）如图2，点P为直线 $x = 5$ 上的一个动点．请从：① $∠ A P B = 3 0^{°}$ ；② $∠ A P B = 4 5^{°}$ ；③ $∠ A P B = 6 0^{°}$ 中任选一个，求出相应的P点坐标；
（ⅱ）如图3，点M为直线 $C D ： y = x + 2$ 上的一个动点，连接 $A M ， B M$ ．当 $∠ A M B$ 最大时，求出此时 $△ M A B$ 的面积．

查看试题解析
18. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x + 6$ 分别交x轴、y轴于点A，B，以AB为直径构造圆，点C在 $\overset{⌢}{O B}$ 上运动，点D在 $\overset{⌢}{A C}$ 上，CD交OA于点P，且 $\hat{C D} = \hat{O A} .$

(1)、求CD的长.

(2)、求证：OP=PD.

(3)、若CE∥OA，交圆于另一点E，连结DE，当△CDE为等腰三角形时，求所有满足条件的点P的坐标。

查看试题解析
19. 如图，直线 $y = - 3 x + 3$ 分别交x轴、y轴于点A，B，以A为圆心， $A B$ 为半径作半圆， $A C ⊥ A B$ 交半圆弧于点C，弦 $C D ∥ x$ 轴，交y轴正半轴于点E，连结 $O D ， B D$ .

(1)、求 $⊙ A$ 的半径长及直线 $B C$ 的函数表达式.

(2)、求 $t a n ∠ A B D$ 的值.

(3)、P为x轴上一点.
①当 $P C$ 平行于四边形 $O A B D$ 的一边时，求出所有符合条件的 $A P$ 的长.
②若直线 $E P$ 恰好平分五边形 $O A C B D$ 的面积，求点P的横坐标.（直接写出答案即可）

查看试题解析