圆与一次函数—浙教版数学九(上)知识点训练
试卷更新日期:2025-01-12 类型:复习试卷
一、选择题
-
1. 已知 , , 三点可以确定一个圆,则以下点坐标不满足要求的是( )A、 B、 C、 D、2. 如图,已知直线y= 与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是( )
 A、30 B、29 C、28 D、273. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)4. 如图, 中, , , , 是 的外接圆,点 是优弧 上任意一点(不包括点 , ),记四边形 的周长为 , 的长为 ,则 关于 的函数关系式是( )
A、30 B、29 C、28 D、273. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)4. 如图, 中, , , , 是 的外接圆,点 是优弧 上任意一点(不包括点 , ),记四边形 的周长为 , 的长为 ,则 关于 的函数关系式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴于点A3 , …,按此做法进行下去,点An的坐标为
 6. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(2,0),直线y=x+与⊙O交于B、C两点,则弦BC的长为 .
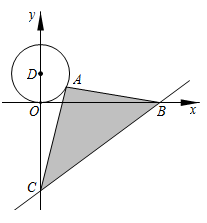
6. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(2,0),直线y=x+与⊙O交于B、C两点,则弦BC的长为 . 7. 如图,直线 与 , 轴分别交于A , B两点,C是以D(2,0)为圆心, 为半径的圆上一动点,连接AC , BC , 则△ABC的面积的最大值是 .
7. 如图,直线 与 , 轴分别交于A , B两点,C是以D(2,0)为圆心, 为半径的圆上一动点,连接AC , BC , 则△ABC的面积的最大值是 . 8. 已知直线 ,点 的坐标为 .过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ,再过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 …按此作法进行下去,点 的坐标为.9. 在平面直角坐标系xOy中,点A是x轴外一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点” .已知⊙P的半径为2,圆心为P(0,t) ,在函数y= x(x>0) 的图象上存在点M,⊙P上存在点N,满足点N是点M的“等距点” ,则t的取值范围为 .
8. 已知直线 ,点 的坐标为 .过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ,再过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 …按此作法进行下去,点 的坐标为.9. 在平面直角坐标系xOy中,点A是x轴外一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点” .已知⊙P的半径为2,圆心为P(0,t) ,在函数y= x(x>0) 的图象上存在点M,⊙P上存在点N,满足点N是点M的“等距点” ,则t的取值范围为 .三、解答题
-
10. 如图,在平面直角坐标系中,以原点О为圆心,3为半径作圆,直线y=mx-m+2与О相交于A,B两点,求弦AB的最小长度.
 11. 如图,在平面直角坐标系中,直线CD:交△ABO的外接圆⊙M于点E,点C,交x轴于点D,交y轴于点F.点C是的中点,连结OC,BC.点A(6,0),点B(0,8).
11. 如图,在平面直角坐标系中,直线CD:交△ABO的外接圆⊙M于点E,点C,交x轴于点D,交y轴于点F.点C是的中点,连结OC,BC.点A(6,0),点B(0,8). (1)、求AB的长和CD的解析式.(2)、求点E的坐标.(3)、点P在x轴上,连结EP,EP与△BCO的任意一边平行时,求OP的长.12. 如图1,在四边形ABCD中, , , , , 点E在AB上,作交BC于点F , 点G为CD上一点,且.如图2,作的外接圆交CD于点H , 连结EH , FH , 设 , .
(1)、求AB的长和CD的解析式.(2)、求点E的坐标.(3)、点P在x轴上,连结EP,EP与△BCO的任意一边平行时,求OP的长.12. 如图1,在四边形ABCD中, , , , , 点E在AB上,作交BC于点F , 点G为CD上一点,且.如图2,作的外接圆交CD于点H , 连结EH , FH , 设 , . (1)、求CD的长.(2)、求y关于x的函数表达式,(3)、当CF与的一边相等时,求满足所有条件的BE的长.13. 如图,在平面直角坐标系中,直线分别交x轴、y轴于点A,B,以AB为直径构造圆,点C在上运动,点D在上,CD交OA于点P,且
(1)、求CD的长.(2)、求y关于x的函数表达式,(3)、当CF与的一边相等时,求满足所有条件的BE的长.13. 如图,在平面直角坐标系中,直线分别交x轴、y轴于点A,B,以AB为直径构造圆,点C在上运动,点D在上,CD交OA于点P,且 (1)、求CD的长.(2)、求证:OP=PD.(3)、若CE∥OA,交圆于另一点E,连结DE,当△CDE为等腰三角形时,求所有满足条件的点P的坐标。14. 如图,在平面直角坐标系中,0为坐标原点,点A、B分别为直线y=- x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC.
(1)、求CD的长.(2)、求证:OP=PD.(3)、若CE∥OA,交圆于另一点E,连结DE,当△CDE为等腰三角形时,求所有满足条件的点P的坐标。14. 如图,在平面直角坐标系中,0为坐标原点,点A、B分别为直线y=- x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC. (1)、求当t为何值时,点Q与点D重合?(2)、设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)、若⊙P与线段QC只有一个交点,请直接写出t的取值范围.15. 如图1,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.
(1)、求当t为何值时,点Q与点D重合?(2)、设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)、若⊙P与线段QC只有一个交点,请直接写出t的取值范围.15. 如图1,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.
 (1)、请直接写出OE、⊙M的半径r、CH的长;(2)、如图2,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;
(1)、请直接写出OE、⊙M的半径r、CH的长;(2)、如图2,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;
(3)、如图3,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a , 始终满足MN·MK=a , 如果存在,请求出a的值;如果不存在,请说明理由.