圆的最值问题—北师大版数学九(下)知识点训练
试卷更新日期:2025-01-12 类型:复习试卷
一、选择题(每题3分,共24分)
-
1. 如图,排水管截面的半径为5分米,水面宽分米, , 则水的最大深度CD为( )
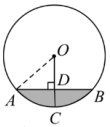 A、 B、 C、 D、2. 如图,在△ABC 中,AB=10,AC=8,BC=6,以边 AB 中点 O 为圆心,作半圆与 AC 相切,点 P,Q 分别是边 BC 和半圆上的动点,连接 PQ,则 PQ 长的最大值与最小 值的差是( )
A、 B、 C、 D、2. 如图,在△ABC 中,AB=10,AC=8,BC=6,以边 AB 中点 O 为圆心,作半圆与 AC 相切,点 P,Q 分别是边 BC 和半圆上的动点,连接 PQ,则 PQ 长的最大值与最小 值的差是( ) A、6 B、 C、9 D、73. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=θ,点E , F分别是AC , BC的中点,直线EF与⊙O交于G , H两点,若⊙O的半径是r , 则GE+FH的最大值是( )
A、6 B、 C、9 D、73. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=θ,点E , F分别是AC , BC的中点,直线EF与⊙O交于G , H两点,若⊙O的半径是r , 则GE+FH的最大值是( ) A、r(2﹣sinθ) B、r(2+sinθ) C、r(2﹣cosθ) D、r(2+cosθ)4. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4.点F为射线CB上一动点,过点C作CM⊥AF于M,交AB于E,D是AB的中点,则DM长度的最小值是( )
A、r(2﹣sinθ) B、r(2+sinθ) C、r(2﹣cosθ) D、r(2+cosθ)4. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4.点F为射线CB上一动点,过点C作CM⊥AF于M,交AB于E,D是AB的中点,则DM长度的最小值是( ) A、 B、 C、 D、5. 已知: 是 的直径, , 是 的切线, 是 上一动点,若 , , ,则 的面积的最小值是( )
A、 B、 C、 D、5. 已知: 是 的直径, , 是 的切线, 是 上一动点,若 , , ,则 的面积的最小值是( ) A、36 B、32 C、24 D、10.46. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.若在△ABC中,AB=AC,BC=6,∠BAC=120°,则△ABC的最小覆盖圆的半径是( )A、3 B、 C、2 D、7. 如图,P为矩形的边的延长线上的动点,于H , 点E在边上,若 , , , 则线段的最大值为( )
A、36 B、32 C、24 D、10.46. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.若在△ABC中,AB=AC,BC=6,∠BAC=120°,则△ABC的最小覆盖圆的半径是( )A、3 B、 C、2 D、7. 如图,P为矩形的边的延长线上的动点,于H , 点E在边上,若 , , , 则线段的最大值为( ) A、 B、 C、 D、8. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )
A、 B、 C、 D、8. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )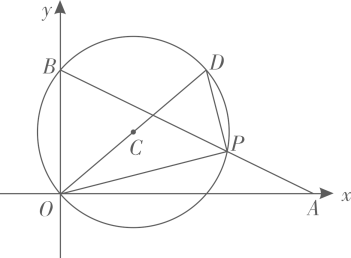 A、 B、2 C、 D、3
A、 B、2 C、 D、3二、填空题(每题3分,共15分)
-
9. 如图,在中, , , 则面积的最大值为 .
 10. 如图,在中, , , , 点P为平面内一点,且 , 过C作交的延长线于点Q , 则的最大值为 .
10. 如图,在中, , , , 点P为平面内一点,且 , 过C作交的延长线于点Q , 则的最大值为 . 11. 在直角中, , , , 点是内一点,满足 , 则的最小值为.
11. 在直角中, , , , 点是内一点,满足 , 则的最小值为. 12. 如图,抛物线与轴负半轴交于点A,P是以点为圆心,半径为2的圆上的动点,是线段PA的中点,连接OQ,则线段OQ的最小值是.
12. 如图,抛物线与轴负半轴交于点A,P是以点为圆心,半径为2的圆上的动点,是线段PA的中点,连接OQ,则线段OQ的最小值是. 13. 如图,点的坐标为 , 点的坐标为 , 点、点关于原点对称,点是平面上一点,且满足 , 则线段的最小值为 .
13. 如图,点的坐标为 , 点的坐标为 , 点、点关于原点对称,点是平面上一点,且满足 , 则线段的最小值为 . 14. 如图,内接于 , 已知是直径, , , 点D在直径上方的半圆上运动,连接交于点E , 则的长度为 , 的最大值为 .
14. 如图,内接于 , 已知是直径, , , 点D在直径上方的半圆上运动,连接交于点E , 则的长度为 , 的最大值为 .
三、解答题(共7题,共61分)
-
15. 如图,有一直径是的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC .
 (1)、求AB的长;(2)、用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,求AP的最小值.
(1)、求AB的长;(2)、用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,求AP的最小值.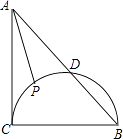 17. 在平面直角坐标系中,对于任意三点给出如下定义:三点中横坐标的最大值与最小值的差我们称为“横距”;三点中纵坐标的最大值与最小值的差我们称之为“纵距”:若三点的横距与纵距相等,我们称这三点为“等距点”.
17. 在平面直角坐标系中,对于任意三点给出如下定义:三点中横坐标的最大值与最小值的差我们称为“横距”;三点中纵坐标的最大值与最小值的差我们称之为“纵距”:若三点的横距与纵距相等,我们称这三点为“等距点”.已知:如图,点 , 点 .
 (1)、在中,与点为等距点的是;(2)、点为轴上一动点,若三点为等距点,求的值;(3)、已知点 , 有一半径为1,圆心为的 , 若上存在点 , 使得三点为等距点,直接写出的取值的范围.18. 【探索发现】有张形状为直角三角形的纸片,小俊同学想用些大小不同的圆形纸片去覆盖这张三角形纸片,经过多次操作发现,如图 , 以斜边为直径作圆,刚好是可以把覆盖的面积最小的圆,称之为最小覆盖圆.
(1)、在中,与点为等距点的是;(2)、点为轴上一动点,若三点为等距点,求的值;(3)、已知点 , 有一半径为1,圆心为的 , 若上存在点 , 使得三点为等距点,直接写出的取值的范围.18. 【探索发现】有张形状为直角三角形的纸片,小俊同学想用些大小不同的圆形纸片去覆盖这张三角形纸片,经过多次操作发现,如图 , 以斜边为直径作圆,刚好是可以把覆盖的面积最小的圆,称之为最小覆盖圆. (1)、【理解应用】我们也可以用一些大小不同的圆覆盖锐角三角形和钝角三角形,请你通过操作探究解决下列问题:如图在中, , 试用直尺和圆规作出这个三角形的最小覆盖圆不写作法,保留作图痕迹 .(2)、【拓展提升】如图 , 在中, , , , 请求出的最小覆盖圆的半径.19. 小学阶段,我们了解到圆:平面上到定点的距离等于定长的所有的点组成的图形叫做圆。在一节数学实践活动课上,老师手拿着三个正方形硬纸板和几个不同的圆形的盘子,他向同学们提出了这样一个问题:已知手中圆盘的直径为 , 手中的三个正方形硬纸板的边长均为 , 若将三个正方形纸板不重叠地放在桌面上,能否用这个圆盘将其盖住?问题提出后,同学们七嘴八舌,经过讨论,大家得出了一致性的结论是:本题实际上是求在不同情况下将三个正方形硬纸板无重叠地适当放置,圆盘能盖住时的最小直径.然后将各种情形下的直径值与进行比较,若小于或等于就能盖住,反之,则不能盖住.老师把同学们探索性画出的四类图形画在黑板上,如图所示.
(1)、【理解应用】我们也可以用一些大小不同的圆覆盖锐角三角形和钝角三角形,请你通过操作探究解决下列问题:如图在中, , 试用直尺和圆规作出这个三角形的最小覆盖圆不写作法,保留作图痕迹 .(2)、【拓展提升】如图 , 在中, , , , 请求出的最小覆盖圆的半径.19. 小学阶段,我们了解到圆:平面上到定点的距离等于定长的所有的点组成的图形叫做圆。在一节数学实践活动课上,老师手拿着三个正方形硬纸板和几个不同的圆形的盘子,他向同学们提出了这样一个问题:已知手中圆盘的直径为 , 手中的三个正方形硬纸板的边长均为 , 若将三个正方形纸板不重叠地放在桌面上,能否用这个圆盘将其盖住?问题提出后,同学们七嘴八舌,经过讨论,大家得出了一致性的结论是:本题实际上是求在不同情况下将三个正方形硬纸板无重叠地适当放置,圆盘能盖住时的最小直径.然后将各种情形下的直径值与进行比较,若小于或等于就能盖住,反之,则不能盖住.老师把同学们探索性画出的四类图形画在黑板上,如图所示. (1)、通过计算,在图1中圆盘刚好能盖住正方形纸板的最小直径应为.(填准确数(2)、图2能盖住三个正方形硬纸板所需的圆盘最小直径为 , 图3能盖住三个正方形硬纸板所需的圆盘最小直径为.(填准确数)(3)、拓展:按图4中的放置,三个正方形放置后为轴对称图形,当圆心落在边上时,圆的直径是多少,请你写出该种情况下求圆盘最小直径的过程,并判断是否能盖住.(计算中可能用到的数据,为了计算方便,本问在计算过程中,根据实际情况最后的结果可对个别数据取整数)20. 课本呈现:如图1,在射门游戏中,球员射中球门的难易程度与他所处的位置对球门的张角()有关.当球员在 , 处射门时,则有张角 . 某数学小组由此得到启发,探究当球员在球门同侧的直线射门时的最大张角.
(1)、通过计算,在图1中圆盘刚好能盖住正方形纸板的最小直径应为.(填准确数(2)、图2能盖住三个正方形硬纸板所需的圆盘最小直径为 , 图3能盖住三个正方形硬纸板所需的圆盘最小直径为.(填准确数)(3)、拓展:按图4中的放置,三个正方形放置后为轴对称图形,当圆心落在边上时,圆的直径是多少,请你写出该种情况下求圆盘最小直径的过程,并判断是否能盖住.(计算中可能用到的数据,为了计算方便,本问在计算过程中,根据实际情况最后的结果可对个别数据取整数)20. 课本呈现:如图1,在射门游戏中,球员射中球门的难易程度与他所处的位置对球门的张角()有关.当球员在 , 处射门时,则有张角 . 某数学小组由此得到启发,探究当球员在球门同侧的直线射门时的最大张角.问题探究:
 (1)、如图2,小明探究发现,若过、两点的动圆与直线相交于点、 , 当球员在处射门时,则有 .
(1)、如图2,小明探究发现,若过、两点的动圆与直线相交于点、 , 当球员在处射门时,则有 .

小明证明过程如下:
设直线交圆于点 , 连接 , 则
∵
∴
∴
(2)、如图3,小红继续探究发现,若过、两点的动圆与直线相切于点 , 当球员在处射门时,则有 , 你同意吗?请你说明理由. (3)、问题应用:如图4,若 , 米,是中点,球员在射线上的点射门时的最大张角为 , 则的长度为米.
(3)、问题应用:如图4,若 , 米,是中点,球员在射线上的点射门时的最大张角为 , 则的长度为米.
(4)、问题迁移:如图5,在射门游戏中球门 , 是球场边线, , 是直角, . 若球员沿带球前进,记足球所在的位置为点 , 求的最大度数.(参考数据: , , , , . )
