圆的折叠问题—北师大版数学九(下)知识点训练
试卷更新日期:2025-01-12 类型:复习试卷
一、选择题(每题3分,共24分)
-
1. 把一张圆纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则弧AB的度数是( )
 A、120° B、135° C、150° D、165°2.
A、120° B、135° C、150° D、165°2.如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
 A、π B、π﹣ C、π﹣ D、π﹣3.
A、π B、π﹣ C、π﹣ D、π﹣3.在⊙O中,AB为直径,点C为圆上一点,将劣弧
 沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( ) A、35° B、40° C、45° D、65°4. 如图, 是 的直径, 是 的弦,先将 沿 翻折交 于点 .再将 沿 翻折交 于点 .若 ,设 ,则 所在的范围是( )
A、35° B、40° C、45° D、65°4. 如图, 是 的直径, 是 的弦,先将 沿 翻折交 于点 .再将 沿 翻折交 于点 .若 ,设 ,则 所在的范围是( )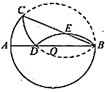 A、 B、 C、 D、5. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
A、 B、 C、 D、5. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
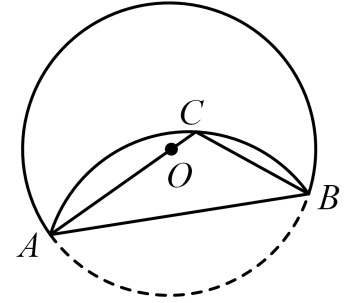 A、 B、 C、 D、6. 如图,在⊙O中,将沿弦AB翻折,使恰好经过圆心O , C是劣弧AB上一点. 已知AE=2,tan∠CBA= , 则AB的长为 ( )
A、 B、 C、 D、6. 如图,在⊙O中,将沿弦AB翻折,使恰好经过圆心O , C是劣弧AB上一点. 已知AE=2,tan∠CBA= , 则AB的长为 ( ) A、 B、6 C、 D、7. 如图, 是 的直径,且 , 是 上一点,将 沿直线 翻折,若翻折后的圆弧恰好经过点 ,则图中阴影部分的面积为( ).
A、 B、6 C、 D、7. 如图, 是 的直径,且 , 是 上一点,将 沿直线 翻折,若翻折后的圆弧恰好经过点 ,则图中阴影部分的面积为( ). A、 B、 C、 D、8. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、8. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、10
A、 B、 C、8 D、10二、填空题(每题3分,共15分)
-
9. 如图,是的直径, , 点C在线段上运动,过点C的弦 , 将沿翻折交直线于点F , 当的长为正整数时,线段的长为 .
 10. 如图,是的弦(不是直径),将沿翻折交于点D.若 , , 则=.
10. 如图,是的弦(不是直径),将沿翻折交于点D.若 , , 则=. 11. 如图.将扇形翻折,使点与圆心重合,展开后折痕所在直线与交于点 , 连接 . 若 , 则图中阴影部分的面积是 .
11. 如图.将扇形翻折,使点与圆心重合,展开后折痕所在直线与交于点 , 连接 . 若 , 则图中阴影部分的面积是 . 12. 如图,正方形的边长为 , 以边上的动点为圆心,为半径作圆,将沿翻折至 , 若过一边上的中点,则的半径为 .
12. 如图,正方形的边长为 , 以边上的动点为圆心,为半径作圆,将沿翻折至 , 若过一边上的中点,则的半径为 . 13. 如图,中, , 斜边 , 以边为直径在另一侧作半圆,点为半圆上一点,将半圆沿所在直线翻折,翻折后的与边相切于点 , 与边相交于点 , 则的长为 .
13. 如图,中, , 斜边 , 以边为直径在另一侧作半圆,点为半圆上一点,将半圆沿所在直线翻折,翻折后的与边相切于点 , 与边相交于点 , 则的长为 .
三、解答题(共7题,共61分)
-
14. 如图,将△ABC沿过点A的直线翻折并展开,点C的对应点C'落在边AB上,折痕为AD , 点O在边AB上,⊙O经过点A、D . 若∠ACB=90°,判断BC与⊙O的位置关系,并说明理由.
 15. 如图, 是 的直径, 为 上一点 ( 不与点 重合), 连结 , 过点 作 , 垂足为点 . 将 沿 翻折, 点 落在点 处得 交 于点 .
15. 如图, 是 的直径, 为 上一点 ( 不与点 重合), 连结 , 过点 作 , 垂足为点 . 将 沿 翻折, 点 落在点 处得 交 于点 . (1)、 求证: 是 的切线.(2)、 若 , 求阴影部分的面积.16. 如图,已知是的直径,弦于点 , 连接 , 将沿翻折得到 , 直线与直线相交于点 .
(1)、 求证: 是 的切线.(2)、 若 , 求阴影部分的面积.16. 如图,已知是的直径,弦于点 , 连接 , 将沿翻折得到 , 直线与直线相交于点 .
 (1)、求证:直线与相切;(2)、若 , 求阴影部分的面积.17. 如图,在中, , , 是上的动点,以为圆心,的长为半径作圆交于点 , 分别是上的点,将沿折叠,点与点恰好重合.
(1)、求证:直线与相切;(2)、若 , 求阴影部分的面积.17. 如图,在中, , , 是上的动点,以为圆心,的长为半径作圆交于点 , 分别是上的点,将沿折叠,点与点恰好重合. (1)、如图1,若 , 证明与直线相切;(2)、如图2,若经过点 , 连接 .
(1)、如图1,若 , 证明与直线相切;(2)、如图2,若经过点 , 连接 .①的长是 ▲ ;
②判断四边形的形状,并证明.
18. 在平面直角坐标系xOy中,将点P沿着y轴翻折,得到的对应点再沿着直线l翻折得到点P1 , 则P1称为点P的“l变换点”. (1)、已知:点P(1,0),直线l:x=2,求点P的“l变换点”的坐标;(2)、若点Q和它的“l变换点”Q1的坐标分别为(2,1)和(3,2),求直线l的解析式;(3)、如图,⊙O的半径为2.
(1)、已知:点P(1,0),直线l:x=2,求点P的“l变换点”的坐标;(2)、若点Q和它的“l变换点”Q1的坐标分别为(2,1)和(3,2),求直线l的解析式;(3)、如图,⊙O的半径为2.①若⊙O上存在点M , 点M的“l变换点”M1在射线 x(x≥0)上,直线l:x=b , 求b的取值范围;
②将⊙O在x轴上移动得到⊙E , 若⊙E上存在点N , 使得点N的“l变换点”N1在y轴上,且直线l的解析式为y= x+1,求E点横坐标的取值范围.
19. 【问题背景】如图 , 在中,将劣弧沿弦所在的直线折叠,使得劣弧恰好过圆心 , 圆心关于直线的对称点为 . (1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.20. 如图1,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以O为圆心,OA的长为半径作半圆,交射线AB于G,连接AE并延长交射线BC于F,连接EG,设OA=x.
(1)、【探究发现】如图 , 连接、 , 并延长交于 , 连接直接写出的度数为 ,与的数量关系为 ;(2)、【深入探究】如图 , 将劣弧沿弦所在的直线折叠,弧不经过圆心 , 在劣弧上取一点不与、重合 , 连接并延长交于点 , 连接、猜想与的数量关系,并说明理由;(3)、【拓展应用】如图 , 在条件下,若平分 , , , 求的长.20. 如图1,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以O为圆心,OA的长为半径作半圆,交射线AB于G,连接AE并延长交射线BC于F,连接EG,设OA=x.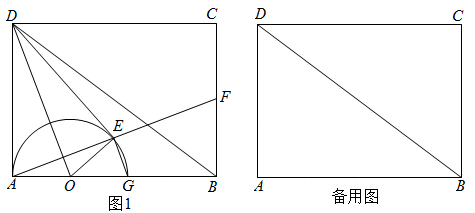 (1)、求证:DE是半圆O的切线;(2)、当点E落在BD上时,求x的值;(3)、当点E落在BD下方时,设△AGE与△AFB面积的比值为y,确定y与x之间的函数关系式;(4)、直接写出:当半圆O与△BCD的边有两个交点时,x的取值范围.
(1)、求证:DE是半圆O的切线;(2)、当点E落在BD上时,求x的值;(3)、当点E落在BD下方时,设△AGE与△AFB面积的比值为y,确定y与x之间的函数关系式;(4)、直接写出:当半圆O与△BCD的边有两个交点时,x的取值范围.