弧长与扇形面积—北师大版数学九(下)知识点训练
试卷更新日期:2025-01-12 类型:复习试卷
一、选择题(每题3分,共24分)
-
1. 如图,点A , B , C在半径为3的⊙O上, , 则的长为( )
 A、3 B、 C、π D、2. 如图,是的内接三角形,若 , , , 则的长为( )
A、3 B、 C、π D、2. 如图,是的内接三角形,若 , , , 则的长为( ) A、 B、 C、 D、3. 如图,在边长为4的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB , AC分别交于E , F两点,求的长为( )
A、 B、 C、 D、3. 如图,在边长为4的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB , AC分别交于E , F两点,求的长为( ) A、 B、 C、 D、4. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC , BD分别与⊙O切于点C , D , 延长AC , BD交于点P . 若∠P=120°,⊙O的半径为6cm , 则图中的长为( )
A、 B、 C、 D、4. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC , BD分别与⊙O切于点C , D , 延长AC , BD交于点P . 若∠P=120°,⊙O的半径为6cm , 则图中的长为( ) A、πcm B、2πcm C、3πcm D、4πcm5. 将一个半径为1的圆形纸片,如图连续对折三次之后,用剪刀沿虚线①剪开,则虚线①所对的圆弧长和展开后得到的多边形的内角和分别为( )
A、πcm B、2πcm C、3πcm D、4πcm5. 将一个半径为1的圆形纸片,如图连续对折三次之后,用剪刀沿虚线①剪开,则虚线①所对的圆弧长和展开后得到的多边形的内角和分别为( ) A、 B、 C、 D、6. 如图是2022年杭州亚运会徽标的示意图,若 , , , 则阴影部分面积为( )
A、 B、 C、 D、6. 如图是2022年杭州亚运会徽标的示意图,若 , , , 则阴影部分面积为( ) A、 B、 C、 D、7. 如图是来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为的斜边BC , 直角边AB , AC . 的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分(两个白色弓形部分)记为Ⅲ.设Ⅰ,Ⅱ,Ⅲ的面积分别为 , , , 则下列结论一定正确的是( )
A、 B、 C、 D、7. 如图是来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为的斜边BC , 直角边AB , AC . 的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分(两个白色弓形部分)记为Ⅲ.设Ⅰ,Ⅱ,Ⅲ的面积分别为 , , , 则下列结论一定正确的是( ) A、 B、 C、 D、8. 如图,两个三角形纸板 , 能完全重合, , , ,将 绕点 从重合位置开始,按逆时针方向旋转,边 , 分别与 , 交于点 , (点 不与点 , 重合),点 是 的内心,若 ,点 运动的路径为 ,则图中阴影部分的面积为( )
A、 B、 C、 D、8. 如图,两个三角形纸板 , 能完全重合, , , ,将 绕点 从重合位置开始,按逆时针方向旋转,边 , 分别与 , 交于点 , (点 不与点 , 重合),点 是 的内心,若 ,点 运动的路径为 ,则图中阴影部分的面积为( )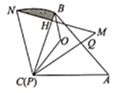 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
9. 如图,已知点C , D是以为直径的半圆的三等分点,半径 , 则扇形的面积为 .
 10. 如图,用一个半径为的定滑轮带动重物上升,滑轮上一点旋转了 , 假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了 .
10. 如图,用一个半径为的定滑轮带动重物上升,滑轮上一点旋转了 , 假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了 . 11. 如图,中, , , , 以为圆心,为半径的圆弧分别交、于点、 , 则图中阴影部分面积之和为 .
11. 如图,中, , , , 以为圆心,为半径的圆弧分别交、于点、 , 则图中阴影部分面积之和为 . 12. 如图,在Rt△ABC中,∠ACB=90°,AC=1,∠A=60°,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DCE,点B经过的路径为 , 将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为弧BF,则图中阴影部分的面积是.(结果保留π)
12. 如图,在Rt△ABC中,∠ACB=90°,AC=1,∠A=60°,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DCE,点B经过的路径为 , 将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为弧BF,则图中阴影部分的面积是.(结果保留π) 13. 如图,是某十字路口机动车转弯时的示意图,设计转弯半径 , 转弯角度 , 大型机动车实际转弯时,转弯半径 , 转弯角度 , 则大型机动车转弯实际行驶路程(的长)与设计转弯行驶路程(AB的长)的差为(结果保留).
13. 如图,是某十字路口机动车转弯时的示意图,设计转弯半径 , 转弯角度 , 大型机动车实际转弯时,转弯半径 , 转弯角度 , 则大型机动车转弯实际行驶路程(的长)与设计转弯行驶路程(AB的长)的差为(结果保留).
三、解答题(共7题,共61分)
-
14. 按要求画出图形:
 (1)、作关于原点中心对称的图形得到;(2)、作绕点逆时针旋转得到 . 且求出点到所经过的路线长.15. 如图,在中, . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是多少?(结果用含的式子表示).
(1)、作关于原点中心对称的图形得到;(2)、作绕点逆时针旋转得到 . 且求出点到所经过的路线长.15. 如图,在中, . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是多少?(结果用含的式子表示). 16. 如图是一款利用曲边三角形制造的扫地机如图是一个曲边三角形,它可按照如下方法作出:作等边三角形 , 分别以点 , , 为圆心,以的长为半径作 , , , 三段弧所围成的图形就是曲边三角形若这个曲边三角形的周长为 , 求它的面积结果保留 .
16. 如图是一款利用曲边三角形制造的扫地机如图是一个曲边三角形,它可按照如下方法作出:作等边三角形 , 分别以点 , , 为圆心,以的长为半径作 , , , 三段弧所围成的图形就是曲边三角形若这个曲边三角形的周长为 , 求它的面积结果保留 . 17. 如图1,的直径 , 在中, , , , 以1cm/s的速度从右向左运动,在运动过程中,点D、E始终在直线上.设运动的时间为t(s),当时,在的右侧, .
17. 如图1,的直径 , 在中, , , , 以1cm/s的速度从右向左运动,在运动过程中,点D、E始终在直线上.设运动的时间为t(s),当时,在的右侧, . (1)、当s时,所在的直线与相切;
(1)、当s时,所在的直线与相切;当s时,所在的直线与相切;
(2)、当所在的直线与相切时,若与有重叠部分,求重叠部分的面积;(3)、当时,如图2,点P是线段上的一个动点,过点P作的一条切线(Q为切点),求线段的最小值.18. 综合与实践【主题】滤纸与漏斗
【素材】如1图所示:

①一张直径为10cm的圆形滤纸;
②一只漏斗口直径与母线均为7cm的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸:
步骤2:按如2图所示步骤折叠好滤纸;

步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如1图所示漏斗中.
【实践探索】
(1)、滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明.(2)、当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留)19. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一如图是从正面看到的一个“老碗”,其横截面可以近似的看成是如图所示的以为直径的半圆 , 为台面截线,半圆与相切于点 , 连结与相交于点水面截线 , , .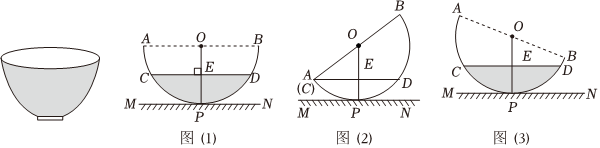 (1)、如图求水深;(2)、将图中的老碗先沿台面向左作无滑动的滚动到如图的位置,使得、重合,求此时最高点和最低点之间的距离的长;(3)、将碗从中的位置开始向右边滚动到图所示时停止,若此时 , 求滚动过程中圆心运动的路径长.20. 如图,在中,连接 , 以为直径的半圆O , 从与共线开始绕点D逆时针旋转,直线与第一次重合时,停止运动,点K是半圆O的中点,连接 , 当 , 与线段有交点时,设交点分别为点P和点Q , 已知 , , .
(1)、如图求水深;(2)、将图中的老碗先沿台面向左作无滑动的滚动到如图的位置,使得、重合,求此时最高点和最低点之间的距离的长;(3)、将碗从中的位置开始向右边滚动到图所示时停止,若此时 , 求滚动过程中圆心运动的路径长.20. 如图,在中,连接 , 以为直径的半圆O , 从与共线开始绕点D逆时针旋转,直线与第一次重合时,停止运动,点K是半圆O的中点,连接 , 当 , 与线段有交点时,设交点分别为点P和点Q , 已知 , , . (1)、求的度数;(2)、当点Q在上时,设 , , 请求出y与x的关系式;(3)、当与重合时,求半圆O与所围成的弓形的面积.
(1)、求的度数;(2)、当点Q在上时,设 , , 请求出y与x的关系式;(3)、当与重合时,求半圆O与所围成的弓形的面积.