弧长与扇形面积—浙教版数学九（上）知识点训练

试卷更新日期：2025-01-12 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 圆心角为 $120 °$ ，半径为3的扇形弧长为（　　）

A、 $\frac{1}{2} π$ B、 $π$ C、 $2 π$ D、 $4 π$

查看试题解析
2. 已知圆心角为120°的扇形的弧长为6π，该扇形的面积为（）

A、 $18 π$ B、 $27 π$ C、 $36 π$ D、 $54 π$

查看试题解析
3. 如图，C ， D是以为直径的半圆周的三等分点，CD=3．则阴影部分的面积等于（）．

A、1.5π B、2π C、π D、2.5π

查看试题解析
4. 如图， $A C ， B C$ 是 $⊙ O$ 的两条弦，点M，N分别是 $A C ， B C$ 的中点，连结 $O M ， O N$ ．若 $⊙ O$ 的半径是6， $∠ C = 100 °$ ，则 $\overset{⌢}{A C B}$ 的长是（）

A、 $\frac{26}{3} π$ B、 $\frac{16}{3} π$ C、 $\frac{13}{3} π$ D、 $\frac{8}{3} π$

查看试题解析
5. 如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点C ，交OB于点D ，若OA＝4，则阴影部分的面积为（　　）

A、 $\frac{4 π}{3}$ B、 $\frac{4 π}{3} + 4 \sqrt{3}$ C、 $\frac{4 π}{3} - 4 \sqrt{3}$ D、 $4 \sqrt{3} - \frac{4 π}{3}$

查看试题解析
6. 如图，在⊙O的内接四边形ABCD中，∠B＝62°，∠ACD＝39°．若⊙O的半径为5，则弧CD的长为（）

A、 $\frac{13}{18} π$ B、 $\frac{10}{9} π$ C、 $\frac{23}{18} π$ D、 $\frac{23}{36} π$

查看试题解析
7. 如图，四边形ABCD是边长为2的正方形，分别以A，B，C，D为圆心，2为半径画圆弧围成如图所示的阴影部分.则阴影部分的周长为（）

A、 $π$ B、 $\frac{1}{3} π$ C、 $\frac{2}{3} π$ D、 $\frac{4}{3} π$

查看试题解析
8. 如果一个扇形的圆心角扩大为原来的2倍，半径扩大为原来的3倍，那么这个扇形的面积将扩大为原来的倍数是（）

A、18 B、12 C、6 D、3

查看试题解析
9. 如图，一张扇形纸片OAB，∠AOB=120°，OA=6，将这张扇形纸片折叠，使点A与点O重合，折痕为CD，则图中未重叠部分(即阴影部分)的面积为（）

A、 $9 \sqrt{3}$ B、 $12 π - 9 \sqrt{3}$ C、 $\frac{9}{2} \sqrt{3}$ D、 $6 π - \frac{9}{2} \sqrt{3}$

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A B = 1 ， B C = \sqrt{3} ， P$ 是 $A D$ 边上的一个动点，连结 $B P$ ，点 $C$ 关于直线 $B P$ 的对称点为 $C_{1}$ ，当 $P$ 运动时， $C_{1}$ 也随之运动．若 $P$ 从 $A$ 运动到 $D$ ，则点 $C_{1}$ 经过的路径长是（）

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{5 \sqrt{3}}{6} π$ C、 $\frac{4 π}{3}$ D、 $\frac{5 π}{3}$

查看试题解析

二、填空题（每题3分，共18分）

11. 一个扇形的弧长是3πcm ，半径是6cm ，则此扇形的圆心角是．

查看试题解析
12. 如图，正五边形ABCDE的边长为2，以A为圆心，AB为半径作 $\overset{⌢}{B E}$ ，则阴影部分的面积为（结果保留T）.

查看试题解析
13. 如图，已知等边 $△ A B C$ 以 $C$ 为旋转中心，按逆时针方向旋转 $α^{°} (0 < α < 180)$ ，得到 $△ D E C$ ，若 $C D ⊥ A B$ ，等边三角形边长为1，则点 $A$ 的运动路径长为.

查看试题解析
14. 如图，四边形ABCD是菱形，∠A=60°，AB=6，扇形BEF的半径为6，圆心角60°，则图中阴影部分的面积是（结果保留π）．

查看试题解析
15. 如图，半圆 $O$ 的直径 $A B = 4$ ，弦 $C D = 2 \sqrt{2}$ ，弦 $C D$ 在半圆上滑动，点 $C$ 从点 $A$ 开始滑动，到点 $D$ 与点 $B$ 重合时停止滑动，若 $M$ 是 $C D$ 的中点，则在整个滑动过程中线段 $B M$ 扫过的面积为.

查看试题解析
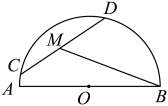16. 量角器和三角板是我们平常数学学习中常用的工具．有一天，爱思考的小聪拿着两块工具拼成了如图1的样子，计划让三角板的直角顶点始终在量角器的半圆弧上运动，紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点，点P为三角板的直角顶点，两直角边PE、PF分别过点A、B．连结CP，过点O作OM⊥CP交CP于点M，交AP于点N若AB=8，则NB的最小值为；若点Q为 $\overset{⌢}{B C}$ 的中点，则点P从点Q运动到点B时，N点的运动路径长为.

查看试题解析

三、解答题（共8题，共72分）

17. 如图，△AOB的顶点都在边长为1的正方形组成的网格格点上，A（-1，3），B（-2，2）

(1)、将ΔAOB绕点O顺时针旋转90°得到A₁OB₁ ，作出旋转后的△A₁OB₁；

(2)、在旋转过程中，点B经过的路径为 $\overset{⌢}{B B_{1}}$ ，求 $\overset{⌢}{B B_{1}}$ 的长（结果保留π）.

查看试题解析
18. 如图，水平放置的圆柱形排水管的截面半径为 $12 c m$ ，截面中有水部分弓形的高为 $6 c m$ ．

(1)、求截面中弦 $A B$ 的长；

(2)、求截面中有水部分弓形的面积．

查看试题解析
19. 如图，以 $△ A B C$ 的一边 $A B$ 为直径作 $⊙ O$ 交 $A C$ 于点 $E$ ， $A B = A C$ ， $⊙ O$ 与 $B C$ 边的交点恰好为 $B C$ 的中点 $D$ ，连结 $D E$ ．

(1)、求证： $D E = C D$ ．

(2)、若 $∠ B A C = 45 ° ， A B = 3$ ，求弧 $D E$ 的长．

查看试题解析
20. 如图，正六边形ABCDEF内接于⊙O，连接AD、CE交于点G，DG=2．

(1)、求正六边形ABCDEF的边长；

(2)、求阴影部分的面积．

查看试题解析
21. 团扇是中国传统工艺品，代表着团圆友善、吉祥如意，某社团组织学生制作团扇，扇面有圆形和正方形两种，每种扇面面积均为 $400 c m^{2}$ .完成扇面后，需对扇面边缘用缎带进行包边处理（接口处长度忽略不计），如图所示：

(1)、圆形团扇的半径为（结果保留 $π$ ） $c m$ ，正方形团扇的边长为 $c m$ ；

(2)、请你通过计算说明哪种形状的扇面所用的包边长度更短.

查看试题解析
22. 现有成 $13 5^{°}$ 角且足够长的墙角和可建总长为15m棚栏的建筑材料来修建花坛.（材料要用完）

(1)、如图1，修建成四边形ABCD的一个花坛，使 $B C / / A D, ∠ C = 9 0^{°}$ .线段BC，CD为新建栅栏，设 $C D = x$ 米，当CD为多少米时，此时花坛的面积最大?

(2)、爱动脑筋的小聪建议：把新建的棚栏建成如图2所示的以 $A$ 为圆心的圆弧BD，这样修建的花坛面积会更大.聪明的你认为小聪的建议合理吗?请说明理由.

查看试题解析
23. 如图①，在Rt△ABC中，∠C=90°，∠A=60°，AC=3cm，边AB在直线l上．将Rt△ABC沿直线l作无滑动翻滚，当Rt△ABC翻滚一周时，求点A经过的路径长要解决这个问题，先要弄清在翻滚时点A经过的路径是什么Rt△ABC翻滚一周即为翻滚三次，第一次翻滚点A经过的路径长是以点B为圆心、AB为半径、圆心角是150°的 $\overset{⌢}{A A_{1}}$ 的长，即为5πcm；第二次翻滚点A经过的路线长是以点C1为圆心、A₁C₁为半径圆心角是90°的 $\overset{⌢}{A_{1} A_{2}}$ 的长，即为 $\frac{3}{2}$ πcm；第三次翻滚时点A没动．所以Rt△ABC翻滚一周点A经过的路径是5π+ $\frac{3}{2}$ π= $\frac{13}{2}$ π(cm)．
思考：如图②，在矩形ABCD中，AB=4，BC=3，边CD在直线l上．将矩形ABCD沿直线l作无滑动翻滚，当点A第一次翻滚到点A1位置时，求点A经过的路径长．

查看试题解析
24. 定义：若圆内接三角形是等腰三角形，我们就称这样的三角形为“圆等三角形”．

(1)、如图1，AB是⊙O的一条弦（非直径），若⊙O在上找一点C，使得△ABC是“圆等三角形”，则这样的点C能找到个．

(2)、如图2，四边形ABCD是⊙O的内接四边形，连结对角线BD，△ABD和△BCD均为“圆等三角形”，且AB=AD．
①当∠A=140°时，求∠ADC的度数；
②如图3，当∠A=120°，AB=6时，求阴影部分的面积．

查看试题解析