【培优卷】浙教版（2024）七上 5.5 一元一次方程的应用 同步练习
试卷更新日期：2025-01-06 类型：同步测试
一、选择题
-
1. 如图，正方形的边长为6，甲、乙两动点分别从正方形 ABCD 的顶点A，C同时沿正方形的边开始运动，甲按顺时针方向环行，乙按逆时针方向环行。若甲的速度是乙的速度的2倍，则它们第2024次相遇是在 ( )
A、点A B、点B C、点C D、点 D2. 某商场出售甲、乙、丙三种型号的电动车，已知甲型车在第一季度的销售额占这三种车总销售额的56%，第二季度乙、丙两种型号的车的销售额比第一季度减少了a%，但该商场电动车的总销售额比第一季度增加了12%，且甲型车的销售额比第一季度增加了23%，则a的值为 ( )A、8 B、6 C、3 D、23. 甲、乙两人分别从相距25km的A，B两地同时出发相向而行.经过4h后，两人尚未相遇，相距1km.再经过1h，乙到A地的距离是甲到B地的距离的3倍，则甲的速度是( )
A、5km/h B、4km/h C、3km/h D、2km/h4. 有一个水池，只打开进水管，2h可把空水池注满；只打开出水管，3h可把满池水放空.若两水管同时打开，则把空水池注满到水池的需要的时间是( )A、3h B、4h C、5h D、6h5. 某省居民生活用电实施阶梯电价，年用电量分为三个阶梯.阶梯电费计价方式如下表：阶梯档次
年用电量
电价
（单位：元/度）
第一阶梯
2 760度及以下部分
0.538
第二阶梯
2 761度至 4 800度部分
0.588
第三阶梯
4 801度及以上部分
0.838
小聪家去年12 月份用电量为500度，电费为319元，则小聪家去年全年用电量为 （ ）
A、5 250度 B、5 100度 C、4 900度 D、4 850度6. 如果，长方形 中有 个形状、大小相同的小长方形，且 ， ，则图中阴影部分的面积为（ ）．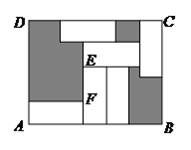
A、 B、 C、 D、7. 我国古代的“九宫图”是由的方格构成的，每个方格均有不同的数，每一行、每一列以及每一条对角线上的三个数之和相等．如图给出了“九宫图”的一部分，请推算的值是（ ）A、 B、 C、 D、8. 下表是某校七~九年级某月课外兴趣小组活动时间统计表，其中各年级同一兴趣小组每次活动时间相同．课外小组活动总时间/h
文艺小组活动次数
科技小组活动次数
七年级
12.5
4
3
八年级
10.5
3
3
九年级
7
a
b
表格中a、b的值正确的是（ ）
A、a=2，b=3 B、a=3，b=2 C、a=3，b=4 D、a=2，b=2二、填空题
-
9. 在一张长方形纸片上剪下一个正方形，剩下一个长方形，称为第一次操作；在剩下的长方形纸片上再剪下一个正方形，剩下一个长方形，称为第二次操作……若在第n次操作后，剩下的长方形为正方形，则称原长方形为 n 阶奇异长方形。如图，在长方形ABCD 中，如果AB=2，BC=6，那么称长方形 ABCD 为2 阶奇异长方形。已知长方形ABCD 的一边长为20，另一边长为a(a<20)，且它是3阶奇异长方形，那么a所有可能的值为。
10. 一个三位数，它的百位上的数比十位上的数的2倍大1，个位上的数比十位上的数的3倍小1.如果把这个三位数的百位上的数字和个位上的数字对调，得到的三位数比原来的三位数大99，那么原来的三位数是.11. 甲、乙两人分别从 两地出发， 相向而行， 出发时他们的速度比是 ， 他们第一次相遇后，甲的速度提高 ，乙的速度减慢 ，这样，当甲到达 地时，乙离 地还有 26 千米， 两地的距离是千米。12. “双十二”某主播直播间推出限时付款优惠活动，优惠规则如上表所示，小王在这次活动中，两次购物总共付款元，第二次购物原价是第一次购物原价的3倍，那么小王这两次购物原价的总和是元．原价
优惠
不超过100元
不打折
超过100元但不超过300元
八折
超过300元
六折
13. 如图，商品条形码是商品的“身份证”，共有位数字．它是由前位数字和校验码构成，其结构分别代表“国家代码、厂商代码、产品代码、校验码”其中，校验码是用来校验商品条形码中前位数字代码的正确性．它的编制是按照特定的算法得来的．其算法为：
步骤：计算前位数字中偶数位数字的和 ， 即；
步骤：计算前位数字中奇数位数字的和 ， 即；
步骤：计算与的和 ， 即；
步骤：取大于或等于且为的整数倍的最小数 ， 即；
步骤：计算与的差就是校验码 ， 即 ．
如图，若条形码中被污染的两个数字的和是 ， 则被污染的两个数字中右边的数字是 ．
三、解答题
-
14. 根据以下素材，尝试解决问题.
出行方式的选择
素材1
随着互联网的普及和城市交通的多样化，人们出行的方式有了更多的选择.某市有出租车、快车和专车三种网约车，收费标准如图(假设网约车行驶的平均速度均为40千米/时).
素材2
1.乘坐网约出租车4千米路程收费为14+2.4×(4-3)=16.4(元).
2.乘坐网约快车4千米路程收费为12+2.5×4+0.4×60×4=24.4(元).
3.网约快车和网约专车在不同时段有各自的优惠方式.
问题解决
问题1
(1)在没有优惠的条件下，如果乘坐这三种网约车的里程数都是10千米，他们发现乘坐出租车最节省钱，费用为 ▲ 元.
问题2
(2)在没有优惠的条件下，如果从甲地到乙地，乘坐出租车比快车节省13.6元，求甲、乙两地间的里程数.
问题3
(3)专车和快车有如下优惠活动：专车收费打八折，另外加5.3元的空车费；快车超过8千米收费减6.5元.如果两位顾客分别乘坐专车、快车行驶相同的里程且收费相同，求这两位顾客乘车的里程数.
15. 如图，在直线l上平放有3个面积相等的长方形，其高分别为2m，3m，6m.现作一平行于l的直线m，使截得三部分阴影面积之和恰好等于一个长方形的面积，求l，m之间的距离.
16. 如图，用大圆布料和小圆布料做成有趣的布贴画，一个布贴画由一个米老鼠和一个毛毛虫组成，一个米老鼠由1块大圆和2块小圆组成，一个毛毛虫由1块大圆和4块小圆组成.现有50块长方形布料，每一块长方形布料有两种剪裁方法：A方法：剪出6个大圆. B方法：剪出24个小圆.
(1)、若将全部长方形布料都按这两种方式剪裁，最多可以做多少幅布贴画? 还剩多少块长方形布料?(2)、若修改剪裁方法，A方法中一个大圆可以改成4个小圆，B方法中4个小圆可以改成1个大圆，问是否存在一种剪裁方案，使得原有的长方形布料所剪下的大圆、小圆正好全部用完?