三角形的外接圆与外心—浙教版数学九（上）知识点训练

试卷更新日期：2025-01-05 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图在△ABC中，边AB，AC的垂直平分线交于点P，连结BP，CP，若∠A=50°，则∠BPC=（）

A、100° B、95° C、90° D、50°

查看试题解析
2. 如图，在正方形方格中，A，B，C，D，E，P均在格点处，则点 $P$ 是下列哪个三角形的外心（）.

A、 $△ A C E$ B、 $△ A B D$ C、 $△ A C D$ D、 $△ B C E$

查看试题解析
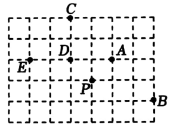3. 已知在Rt△ABC中，∠C=90°，AC=5，BC=12，则△ABC的外接圆直径为（）

A、5 B、12 C、13 D、6.5

查看试题解析
4. 点 $O$ 是 $△ A B C$ 的外心，也是 $△ B C D$ 的内心，若 $∠ A = 70 °$ ，则 $∠ B D C$ 的度数是（）

A、80° B、90° C、100° D、110°

查看试题解析
5. 《九章算术》中“今有勾八步，股有十五步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步．问该直角三角形的容圆（外接圆）直径是多少？”（）

A、14步 B、15步 C、16步 D、17步

查看试题解析
6. 如果一个三角形的外心在三角形的外部，那么这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
7. 已知直角三角形的两条边长为6和8，则其外接圆的半径为．

查看试题解析
8. （1）尺规作图，作出 $△ A B C$ 的外接圆（不写作图过程，但保留作图痕迹）；
（2）若 $∠ B = 45 ° ， A C = 2$ ，求 $△ A B C$ 外接圆的半径长．

查看试题解析
9. 如图，在等腰直角 $△ A B C$ 中，P是斜边BC上一点（不与点B ， C重合），PE是 $△ A B P$ 的外接圆 $⊙ O$ 的直径．

(1)、求 $∠ A P E$ 的度数．

(2)、若 $⊙ O$ 的直径为2，求 $P C^{2} + P B^{2}$ 的值．

查看试题解析

二、能力提升

10. 直角三角形的外接圆半径为3，内切圆半径为1，则该直角三角形的周长是（）

A、12 B、14 C、16 D、18

查看试题解析
11. 如图，以 $A B$ 为直径的 $⊙ O$ 与 $C B$ 相切于点B ，连接 $A C$ 交 $⊙ O$ 于点D ，点E为 $B C$ 边中点，连接 $D E$ 交 $O C$ 于点 $P$ ．若 $⊙ O$ 的半径为4， $D E = 3$ ．则 $\frac{O P}{C P}$ 的值为（）

A、 $\frac{18}{25}$ B、 $\frac{25}{18}$ C、 $\frac{25}{32}$ D、 $\frac{32}{25}$

查看试题解析
12. 如图，O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是（）

A、130° B、140° C、150° D、160°

查看试题解析
13. 三角形三边长为5，5，6，则这个三角形的外心 $O_{1}$ 和重心 $O_{2}$ 的距离为.

查看试题解析
14. 如图，△ABC是⊙O的内接等腰三角形，∠ABC=30°，弦EF过AB边的中点D ，且EF∥BC ，若BC＝ $2 \sqrt{3}$ ，则外接圆的半径为， EF=.

查看试题解析
15. 如图所示的网格由边长均为1的小正方形组成，点A、B、C、D、E、F在小正方形的顶点上，则 $△ A B C$ 外接圆的圆心是点，弧 $A C$ 的长是.

查看试题解析
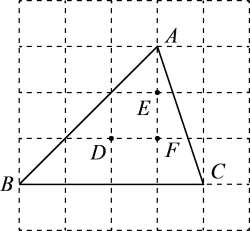16. 如图1，已知抛物线 $y = x^{2} + b x + c$ 经过原点 $O$ ，它的对称轴是直线 $x = 2$ ，动点 $P$ 从抛物线的顶点 $A$ 出发，在对称轴上以每秒 $1$ 个单位的速度向上运动，设动点 $P$ 运动的时间为 $t$ 秒，连接 $O P$ 并延长交抛物线于点 $B$ ，连接 $O A$ ， $A B$ .

(1)、求抛物线的函数解析式；

(2)、当 $△ A O B$ 为直角三角形时，求 $t$ 的值；

(3)、如图2， $⊙ M$ 为 $△ A O B$ 的外接圆，在点 $P$ 的运动过程中，点 $M$ 也随之运动变化，请你探究：在 $1 \leq t \leq 5$ 时，求点 $M$ 经过的路径长度.

查看试题解析

三、拓展创新

17. 定义：若两个三角形中，有两组边对应相等且其中一组等边所对的角对应相等，但不是全等三角形，我们就称这两个三角形为偏等三角形．

(1)、如图1，点C是 $\overset{⌢}{B D}$ 的中点，∠DAB是 $\overset{⌢}{B D}$ 所对的圆周角，AD＞AB，连结AC、DC、CB，试说明△ACB与△ACD是偏等三角形．

(2)、如图2，△ABC与△DEF是偏等三角形，其中∠A＝∠D，AC＝DF，BC＝EF，则∠B+∠E＝.请填写结论，并说明理由．

(3)、如图3，△ABC内接于⊙O，AC＝4，∠A＝30°，∠B＝105°，若点D在⊙O上，且△ADC与△ABC是偏等三角形，AD＞CD，求AD的值．

查看试题解析