浙教版数学八年级上学期期末模拟卷（三）

试卷更新日期：2025-01-05 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 函数 $y = \frac{\sqrt{x}}{x - 1}$ 的自变量 $x$ 的取值范围是（）

A、 $x \geq 0$ B、 $x \neq 1$ C、 $x \geq 0$ 且 $x \neq 1$ D、 $x > 1$

查看试题解析
2. 若 $a > b - 1$ ，则下列结论一定正确的是（）

A、 $a + 1 < b$ B、 $a - 1 < b$ C、 $a > b$ D、 $a + 1 > b$

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ，以点A为圆心，适当长为半径画弧分别交 $A B$ ， $A C$ 于点M和点N ，再分别以点M ， N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P ，连接 $A P$ 并延长交 $B C$ 于点D.若 $△ A C D$ 的面积为8，则 $△ A B D$ 的面积是( )

A、8 B、16 C、12 D、24

查看试题解析
4. 不等式组 ${\begin{array}{l} 2 x \geq x - 1 \\ \frac{x + 1}{2} > \frac{2 x}{3} \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 在平面直角坐标系中，点P(1，2)关于原点的对称点P'的坐标是（）

A、(1，2) B、(-1，2) C、(1，-2) D、(-1，-2)

查看试题解析
6. 若不等式组 ${\begin{array}{l} x + 6 < 4 x - 3 \\ x > m \end{array}$ 的解集是 $x > 3$ ，则m的取值范围是（）

A、 $m > 3$ B、 $m \geq 3$ C、 $m \leq 3$ D、 $m < 3$

查看试题解析
7. 如果点P（m，1+2m）在第三象限内，那么m的取值范围是（）

A、 $- \frac{1}{2} < m < 0$ B、 $m > - \frac{1}{2}$ C、 $m < 0$ D、 $m < - \frac{1}{2}$

查看试题解析
8. 正比例函数 $y = k x (k \neq 0)$ 的图象如图所示，则k的值可能是( )

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $- 1$ D、 $- \frac{1}{3}$

查看试题解析
9. 若一次函数 $y = 2 x + 1$ 的图象经过点 $(- 3 ， y_{1})$ ， $(4 ， y_{2})$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} \leq y_{2}$ D、 $y_{1} \geq y_{2}$

查看试题解析
10. 第11届中国（湖南）矿物宝石国际博览会在我市举行，小方一家上午 $9 ： 00$ 开车前往会展中心参观．途中汽车发生故障，原地修车花了一段时间．车修好后，他们继续开车赶往会展中心．以下是他们家出发后离家的距离 $s$ 与时间的函数图象．分析图中信息，下列说法正确的是（　　）

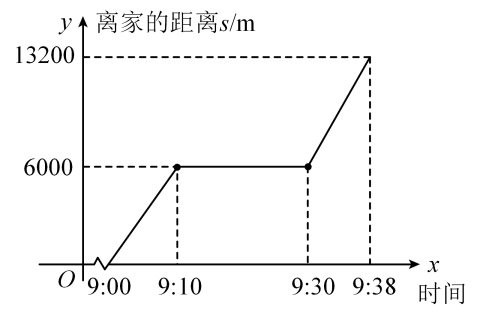A、途中修车花了 $30 m i n$ B、修车之前的平均速度是 $500 m$ / $m i n$ C、车修好后的平均速度是 $80 m$ / $m i n$ D、车修好后的平均速度是修车之前的平均速度的 $1.5$ 倍

查看试题解析

二、填空题（每题3分，共18分）

11. 在平面直角坐标系中，若一次函数的图象经过第一、二、三象限，请写出一个符合该条件的一次函数的表达式．

查看试题解析
12. 如图，在 $▱ A B C D$ 中， $A B = 4, A D = 5, ∠ A B C = 3 0^{°}$ ，点 $M$ 为直线BC上一动点，则 $M A + M D$ 的最小值为．

查看试题解析
13. 若关于x的不等式组 ${\begin{array}{l} 2 x + 1 > x + a ① \\ \frac{x}{2} + 1 \geq \frac{5}{2} x - 9 ② \end{array}$ 所有整数解的和为 $14$ ，则整数 $a$ 的值为．

查看试题解析
14. 如图，直线 $y = k x - 2 k + 3$ （k为常数， $k < 0$ ）与x，y轴分别交于点A，B，则 $\frac{2}{O A} + \frac{3}{O B}$ 的值是．

查看试题解析
15. 如图，在一个平面区域内，一台雷达探测器测得在点A ， B ， C处有目标出现．按某种规则，点A ， B的位置可以分别表示为（1，90°），（2，240°），则点C的位置可以表示为．

查看试题解析
16. 某公司生产了A ， B两款新能源电动汽车．如图，l₁ ， l₂分别表示A款，B款新能源电动汽车充满电后电池的剩余电量y（kw•h）与汽车行驶路程x（km）的关系．当两款新能源电动汽车的行驶路程都是300km时，A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 kw•h ．

查看试题解析

三、解答题（共8题，共72分）

17. 求不等式组 ${\begin{array}{l} 2 x \leq 3 x - 1 ， \\ 1 + 3 (x - 1) < 2 (x + 1) \end{array}$ 的解集，并把它的解集表示在数轴上．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 3 (x - 1) \geq 2 x - 5 ， ① \\ 2 x < \frac{x + 3}{2} ， ② \end{array}$ 并写出它的所有整数解．

查看试题解析
19. 江南农场收割小麦，已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷，2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷．

(1)、每台大型收割机和每台小型收割机1小时收割小麦各多少公顷？

(2)、大型收割机每小时费用为300元，小型收割机每小时费用为200元，两种型号的收割机一共有10台，要求2小时完成8公顷小麦的收割任务，且总费用不超过5400元，有几种方案？请指出费用最低的一种方案，并求出相应的费用．

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，直线l经过 $A (0, 4)$ 和 $B (- 2, 0)$ 两点．

(1)、在同一坐标系中描出点 $C (4, 2)$ ，直接写出点C关于x轴的对称点E的坐标；

(2)、点D在坐标轴上，且 $△ A B O$ 与 $△ O C D$ 全等，则点D的坐标为；

(3)、若已知点 $F (1, 2)$ ，则 $△ A B F$ 的面积为．

查看试题解析
21. 在 $△ A B C$ 中， $∠ C = ∠ B = 5 0^{°}$ ，点 $D$ 在边BC上运动（点D不与点B，C重合），连接AD，在 $△ A D C$ 内部作 $∠ A D E = 5 0^{°}, D E$ 与AC边相于点 $E$ .
（I）如图1，当 $∠ B D A = 10 0^{°}$ 时， $∠ E D C =$ ▲ （度）， $∠ A E D =$ ▲ （度）；
（II）如图2，若 $A C = D C$ ，证明： $△ A B D ≅ △ D C E$ ；
（III）在点 $D$ 的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，直接写出此时 $∠ B D A$ 的度数；若不可以，请说明理由.

查看试题解析
22. 如图，在平面直角坐标系中，已知A（a，0）， B（b，0），其中a，b满足 $\sqrt{b - 3} + | a + 1 | = 0,$ 点 M为第三象限内的一点.

(1)、直接写出A，B两点的坐标；

(2)、若点 M（-2，m），请用含 m的式子表示△ABM的面积

(3)、若点.M（2-m，2m-10）到坐标轴的距离相等，且 $M N ‖ A B, M N = A B,$ ，求点N的坐标.

查看试题解析
23. 如图1，平面直角坐标系中，一次函数 $y = \frac{1}{2} x + 3$ 图像分别交 $x$ 轴、 $y$ 轴于点A、B，一次函数 $y = - x + b$ 的图像经过点 $B$ ，并与 $x$ 轴交于点 $C$ ，点 $P$ 是直线AB上的一个动点.

(1)、求直线BC的表达式与点C的坐标；

(2)、如图2，过点P作x轴的垂线，交直线BC于点Q，垂足为点H，试探究直线AB上是否存在点P，使PQ=BC?若存在，求出点P的坐标，说明理由.

(3)、试探究x轴上是否存在点M，使以A，B，M为顶点的三角形是等腰三角形.若存在，请求出M点的坐标，若不存在，请说明理由.

查看试题解析