【培优版】北师大版数学八年级上册 7.5三角形内角和定理 同步练习
试卷更新日期:2025-01-05 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC
上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF; ②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE
④.若BE平分∠ABC,则FG=;
 A、①②③ B、③④ C、①②④ D、①②③④2. 如图,在中, , , 的平分线交于点O,的外角的平分线所在直线与的平分线交于点D,与的外角的平分线交于点E.有下列结论∶①;②;③;④ . 其中正确的结论有( )
A、①②③ B、③④ C、①②④ D、①②③④2. 如图,在中, , , 的平分线交于点O,的外角的平分线所在直线与的平分线交于点D,与的外角的平分线交于点E.有下列结论∶①;②;③;④ . 其中正确的结论有( ) A、1个 B、2 个 C、3个 D、4个3. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A、1个 B、2 个 C、3个 D、4个3. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( ) A、① B、①② C、①②③ D、①②④4. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )
A、① B、①② C、①②③ D、①②④4. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )①;②;③;④ .
 A、①② B、②③④ C、①③④ D、①②③④5. 如图,△ABC中,AB=AC , 点E , F分别为边AB , BC上的点,将△BEF沿EF折叠得△PEF , 连结AP , CP , 过点P作PD⊥AC于点D , 点D恰好是AC的中点.若∠BAC=50°,AP平分∠BAC , 则∠PFC=( )
A、①② B、②③④ C、①③④ D、①②③④5. 如图,△ABC中,AB=AC , 点E , F分别为边AB , BC上的点,将△BEF沿EF折叠得△PEF , 连结AP , CP , 过点P作PD⊥AC于点D , 点D恰好是AC的中点.若∠BAC=50°,AP平分∠BAC , 则∠PFC=( ) A、100° B、90° C、80° D、60°6. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:;;;;其中正确的说法有( )
A、100° B、90° C、80° D、60°6. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:;;;;其中正确的说法有( ) A、4个 B、3个 C、2个 D、1个7. 如图,分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记 , 当最小时,则关于的数量关系正确的是( )
A、4个 B、3个 C、2个 D、1个7. 如图,分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记 , 当最小时,则关于的数量关系正确的是( ) A、 B、 C、 D、8. 如图,在四边形中, , 若的平分线交于点 , 连接 , 且平分 , 则下列结论:①;②为的中点;③;④ , 其中正确的是( ).
A、 B、 C、 D、8. 如图,在四边形中, , 若的平分线交于点 , 连接 , 且平分 , 则下列结论:①;②为的中点;③;④ , 其中正确的是( ). A、①②③ B、①③④ C、②③④ D、①②③④
A、①②③ B、①③④ C、②③④ D、①②③④二、填空题
-
9. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
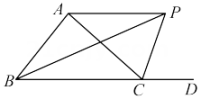 10. 如图,在四边形中, , , , 点M , N分别在 , 上,当的周长最小时,的度数为度.
10. 如图,在四边形中, , , , 点M , N分别在 , 上,当的周长最小时,的度数为度. 11. 在中, , , 在的延长线上有一点使得 , 过点作的垂线,垂足为 , 若 , 则 .
11. 在中, , , 在的延长线上有一点使得 , 过点作的垂线,垂足为 , 若 , 则 . 12. 如图, , 点、分别是边、上的定点,点、分别是边、上的动点,记 , , 当最小时,则的值为.
12. 如图, , 点、分别是边、上的定点,点、分别是边、上的动点,记 , , 当最小时,则的值为.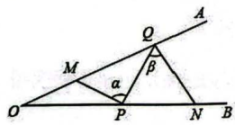 13. 如图①,点分别为长方形纸带的边上的点, , 将纸带沿折叠成图②(为和的交点),再沿折叠成图③(为和的交点),则图③中的(结果用含的代数式表示).
13. 如图①,点分别为长方形纸带的边上的点, , 将纸带沿折叠成图②(为和的交点),再沿折叠成图③(为和的交点),则图③中的(结果用含的代数式表示).
三、解答题
-
14. 在△ABC中,AB=AC , ∠BAC=α,D是直线BC上一点(不与点B , C重合),以AD为边在AD的右侧作△ADE , 使AD=AE , ∠DAE=∠BAC , 连接CE .

(1)、【发现】如图1,点D在线段BC上.①求证:△ABD≌△ACE;
②当∠BAC=100°时,求∠BCE的度数;
(2)、【探究】在点D的运动过程中,当DE垂直于△ABC的某边所在直线时,求∠DEC的度数.(用含α的式子表示)15. 在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如的三角形是“智慧三角形”.如图, , 在射线上找一点A,过点作交于点 , 以为端点作射线 , 交射线于点 . (1)、的度数为_______°,______(填“是”或“不是”)智慧三角形;(2)、若 , 求证:为“智慧三角形”;(3)、当为“智慧三角形”时,求的度数.16. 如图 , 在中,与的平分线相交于点 .
(1)、的度数为_______°,______(填“是”或“不是”)智慧三角形;(2)、若 , 求证:为“智慧三角形”;(3)、当为“智慧三角形”时,求的度数.16. 如图 , 在中,与的平分线相交于点 . (1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.17. 如图,已知 , 现将一直角三角形放入图中,其中 , 交于点 , 交于点
(1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.17. 如图,已知 , 现将一直角三角形放入图中,其中 , 交于点 , 交于点(1)当所放位置如图①所示时,则与的数量关系为_______;请说明理由.
(2)当所放位置如图②所示时,与的数量关系为________;
(3)在(2)的条件下,若与交于点O,且 , , 求的度数.
 18. 如图1,将一张宽度相等的纸条()按如图所示方式折叠,记点C,D的对应点分别为 , , 折痕为 , 且交于点G.
18. 如图1,将一张宽度相等的纸条()按如图所示方式折叠,记点C,D的对应点分别为 , , 折痕为 , 且交于点G. (1)、若 , 则______度.(2)、如图 , 在(1)的条件下,将四边形沿向下翻折,记 , 的对应点分别为 , . 再将长方形沿着翻折,记的对应点分别为 , , 折痕为(点在上,点在上).若 , 求的度数.(3)、如图 , 分别作 , 的平分线交于点 , 连结作的平分线交于点 , 延长交于点 . 若 , 比多27°,求的度数
(1)、若 , 则______度.(2)、如图 , 在(1)的条件下,将四边形沿向下翻折,记 , 的对应点分别为 , . 再将长方形沿着翻折,记的对应点分别为 , , 折痕为(点在上,点在上).若 , 求的度数.(3)、如图 , 分别作 , 的平分线交于点 , 连结作的平分线交于点 , 延长交于点 . 若 , 比多27°,求的度数

