代数式与一元一次方程综合与实践题—广东省（人教版）数学七（上）期末复习

试卷更新日期：2025-01-04 类型：复习试卷

进入出卷网下载

一、代数式

1. 综合与实践：
主题：制作一个无盖长方形盒子.
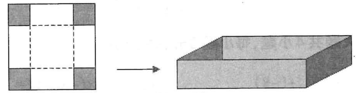
步骤1：按照如图所示的方式，将正方形纸片的四个角剪掉四个大小相同的小正方形.
步骤2：沿虚线折起来，就可以做成一个无盖的长方体盒子.

(1)、【问题分析】
如果原正方形纸片的边长为 $a$ ，剪去的正方形的边长为 $b$ ，则折成的无盖长方体盒子的高、底面积、容积分别为、、(请你用含a，b的代数式来表示).

(2)、如果a=20cm，剪去的小正方形的边长按整数值依次变化，即分别取 $1 c m ， 2 c m ， 3 c m$ ， $4 c m ， 5 c m ， 6 c m ， 7 c m ， 8 c m ， 9 c m ， 10 c m$ 时，折成的无盖长方体的容积分别是下表数据，请求出 $m$ 和 $n$ 分别是多少?
剪去正方形的边长 $/ c m$
1
2
3
4
5
6
7
8
9
10
容积 $/ c m^{3}$
324
512
m
n
500
384
252
128
36
0

(3)、【实践分析】
观察绘制的统计表，你发现，随着减去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时，所得的无盖长方体的容积最大，此时最大容积是多少?

查看试题解析
2. 再读教材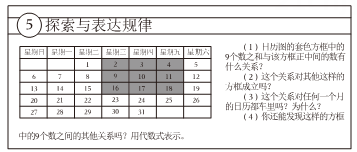
请解答教材中的(1)、(2)问。
活学活用
小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数 $2 ， 4 ， 6 ， 8 ， ⋯$ ，排成如图形式，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：

(1)、十字框中的五个数的和与中间的数16有什么关系?

(2)、设中间的数为 $x$ ，用代数式表示十字框中的五个数的和；

(3)、若将十字框上下左右移动，可框住另外的五个数，其它五个数的和能等于2010吗?如能，写出这五个数，如不能，说明理由.

查看试题解析
3. 某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为a $c m$ 的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒，纸板厚度及接缝处忽略不计）．
操作一：根据图1方式制作一个无盖的长方体盒子，方法是：先在纸板四角剪去四个同样大小边长为b $c m$ 的小正方形，再沿虚线折合起来．并设该长方体的长、宽、高之和为 $S_{1}$ ．
操作二：根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为bcm的小正方形和两个同样大小的小长方形，再沿虚线折合起来．并设该长方体的长、宽、高之和为 $S_{2}$ ．

(1)、按照操作一，若 $a = 12 c m$ ， $b = 3 c m$ ，则 $S_{1} =$ ；

(2)、按照操作二，则 $S_{2} =$ ；（用含a ， b的代数式表示）

(3)、现有两张边长为 $a c m$ 的正方形纸板，分别按操作一和操作二的要求制作两个长方体盒子，问： $S_{1}$ 与 $S_{2}$ 的值能相等吗？请说明理由．

查看试题解析
4. 综合与实践：在学习《整式的加减》时，我们探究了月历中数字之间的关系和变化规律．已知月历中同行的数从左向右依次递增1，同列的数从上向下依次递增7．

(1)、探究1  图1是某月的月历，现要探究带阴影的“口”字方框中的4个数（框中圈出的数没有空白）的数量关系，方框可以任意移动；小明是先假设左上角的数为m ，他通过计算发现斜对角的两个数字之和均为，从而他得出结论：“口”字方框中的4个数满足斜对角两数之和（填“相等”或“不相等”）；

(2)、探究2  小明又探究了图2中带阴影的十字方框中的5个数（框中圈出的数没有空白）的数量关系，发现当十字框任意移动位置时这5个数之和总是5的倍数，请你通过计算说明他的结论成立的理由；

(3)、探究3  小明还探究了在图3中任意选取“H”形框中的7个数（如阴影部分所示）的规律，他认为这7个数的和可以是133，你认为他的说法正确吗？并说明理由．

查看试题解析
5. 综合与实践：观察下图，解答下列问题，

(1)、图1的一些圆圈被直线分层显示前面4层，第一层有1个圆圈，第二层有3个圆圈，第三层有5个圆圈，…，如果要你继续画下去，第6层有个圆圈；第 $n$ 层有个圆圈；

(2)、对比图1图2，感受图形的转化，数图中的圆圈个数可以有多种不同的方法.比如：前两层的圆圈个数和为 $(1 + 3)$ 或 $2^{2}$ ，由此得， $1 + 3 = 2^{2}$ ，总结规律，从1开始的 $n$ 个连续奇数之和是多少？用 $n$ 的代数式把它表示出来：．

(3)、运用（2）中的规律计算： $41 + 43 + 45 + \cdot \cdot \cdot + 199$ ．

查看试题解析
6. 【问题提出】数学活动课上，小寻提出一个猜想：设一个三位数的百位数字是a ，十位数字是b ，个位数字是c ．若 $a + b + c$ 可以被9整除，则这个数可以被9整除．
【试一试】135可以被9整除， $1 + 3 + 5 = 9$ ，可以被9整除；
297可以被9整除， $2 + 9 + 7 = 18$ ，可以被9整除；
【探索验证】

(1)、这个三位数用含a ， b ， c的代数式表示为：．

(2)、小寻的猜想对吗？若对，请用代数式的知识证明这个猜想：若不对，请说明理由．

(3)、【实践应用】同学小佳练习时遇到了这样一个问题：已知四位数231m能被9整除，题目中四位数的最后一位数m不清晰，请你括小佳写出这个数字m是．

查看试题解析
7. 综合与实践：
主题：制作一个无盖长方形盒子．
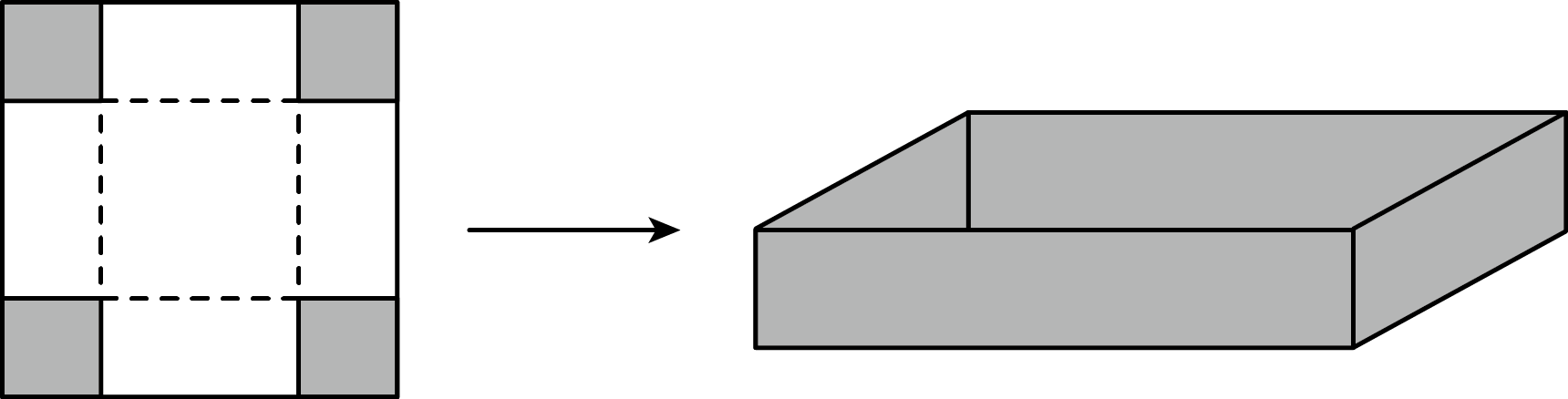
步骤1：按照如图所示的方式，将正方形纸片的四个角剪掉四个大小相同的小正方形．
步骤2：沿虚线折起来，就可以做成一个无盖的长方体盒子．

(1)、【问题分析】
如果原正方形纸片的边长为a，剪去的正方形的边长为b，则折成的无盖长方体盒子的高、底面积、容积分别为、、（请你用含a，b的代数式来表示）．

(2)、【实践探索】
如果 $a = 20 c m$ ，剪去的小正方形的边长按整数值依次变化，即分别取 $1 c m$ ， $2 c m$ ， $3 c m$ ， $4 c m$ ， $5 c m$ ， $6 c m$ ， $7 c m$ ， $8 c m$ ， $9 c m$ ， $10 c m$ 时，折成的无盖长方体的容积分别是下表数据，请求出m和n分别是多少？
剪去正方形的边长/ $c m$
1
2
3
4
5
6
7
8
9
10
容积/ $c m^{3}$
324
512
m
n
500
384
252
128
36
0

(3)、【实践分析】
观察绘制的统计表，你发现，随着减去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化？并分析猜想当剪去图形的边长为多少时，所得的无盖长方体的容积最大，此时最大容积是多少？

查看试题解析
8.

(1)、再读教材
如图是某月的日历．
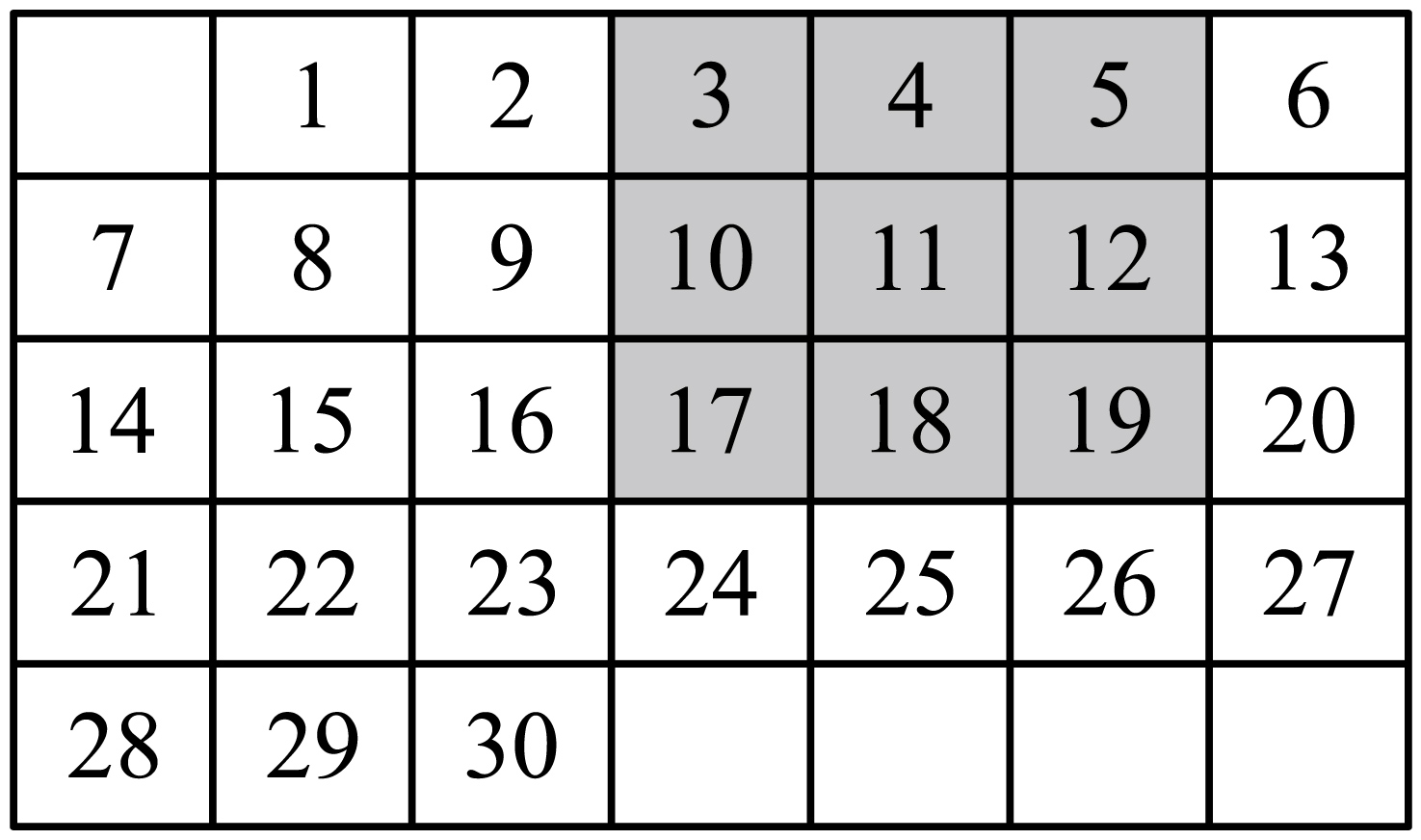
①带阴影的方框中的9个数之和与方框正中的数有什么关系？
②不改变方框的大小如果将带阴影的方程移至其他几个位置试一试，上述关系还成立吗？如成立，请说明为什么成立．

(2)、活学活用
小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数2，4，6，8，…，排成如图形式，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：
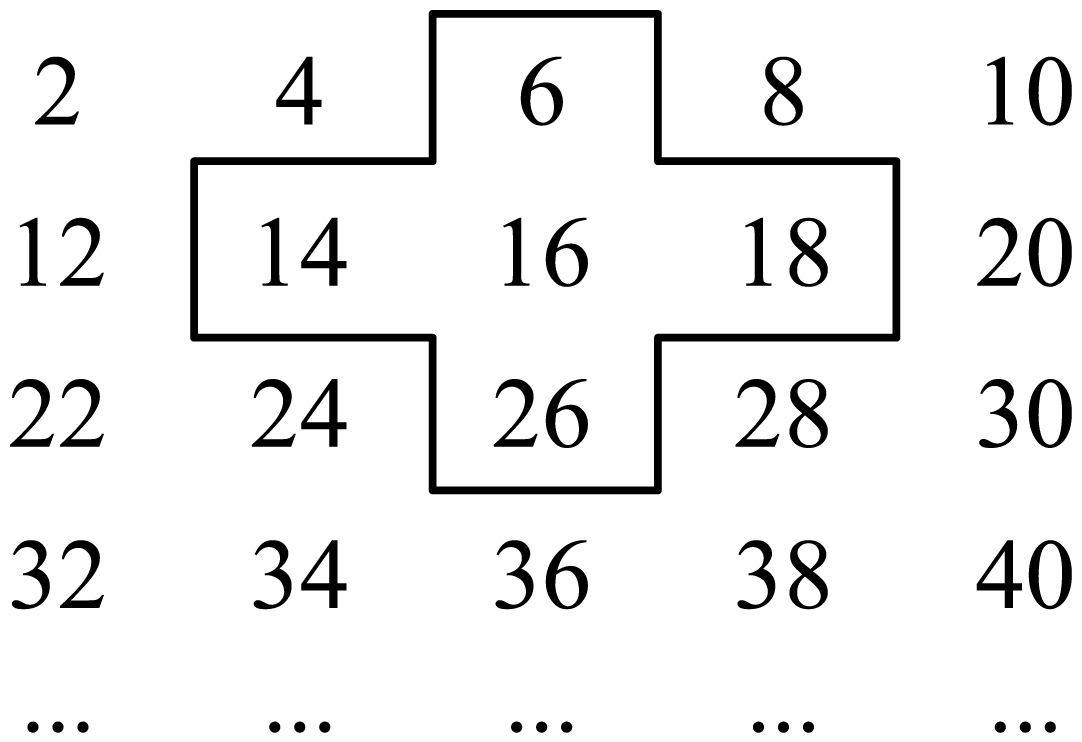
①十字框中的五个数的和与中间的数16有什么关系？
②设中间的数为x，用代数式表示十字框中的五个数的和；
③若将十字框上下左右移动，可框住另外的五个数，其它五个数的和能等于2010吗？如能，写出这五个数，如不能，说明理由．

查看试题解析
9. 综合探究：
整体思想是一种重要的数学思想方法，其思维方式是根据问题的结构特征，把一组数，一个代数式或几个图形视为一个整体，去观察，分析，解决问题的一种方法．这样做，不仅简化解题过程，提高思维能力，还往往可以解决按常方法解决不了的一些问题．
如：代数式 $4 (a + b) + 2 (a + b) - (a + b)$ 的化简问题．若把 $(a + b)$ 看成一个整体，
则： $4 (a + b) + 2 (a + b) - (a + b) = (4 + 2 - 1) (a + b) = 3 (a + b) = 3 a + 3 b$ ．
这就是数学解题中的“整体思想”．
请运用上面的“整体思想”解决下列问题：

(1)、尝试应用：化简 $5 (x + y)^{2} - 7 (x + y) + 2 (x + y)^{2} + 6 (x + y)$

(2)、拓展运用：如图1，点O是线段 $A B$ 上一点，C、D分别是线段 $A O 、 B O$ 的中点，当 $A B = 16$ 时，求线段 $C D$ 的长度．

(3)、迁移运用：如图2，长方形纸片 $A B C D$ ，点E ， F分别是边 $A B ， C D$ 上任意一点，连接 $E F$ ．将 $∠ B E F$ 对折，点B落在直线 $E F$ 上的点 $B^{'}$ 处，得折痕 $E M$ ；将 $∠ A E F$ 对折，点A落在直线 $E F$ 上的点 $A^{'}$ 处，得折痕 $E N$ ， $∠ N E M$ 的度数会随着折痕的变化而变化吗？说明你的理由．

查看试题解析

二、一元一次方程

10. 综合与实践：

商品条形码在生活中随处可见，它是商品的身份证.条形码是由13位数字（每个数字都是由大于等于0且小于等于9的整数）组成，前12位数字分别表示“国家代码、出口商识别码和商品代码”相关信息，如图①693是代表中国，49170代表出口商识别码，0940代表商品代码，第13位数字2为“校验码”.其中，校验码是用来校验商品条形码中前12位数字代码的正确性，它的编制是按照特定算法得来的，具体算法如下（以图①为例）：

步骤	举例说明
步骤1：自左向右编号：	某商品的条形码：693489170940X（X为校验码）
	位置序号	1	2	3	4	5	6	7	8	9	10	11	12	13
	代码	6	9	3	4	9	1	7	0	0	9	4	0	X
步骤2：求前12位数字中偶数位上的数字之和s；	$s = 9 + 4 + 1 + 0 + 9 + 0 = 23$ ；
步骤3：求前12为数字钟奇数位上的数字之和t；	$t = 6 + 3 + 9 + 7 + 0 + 4 = 29$ ；
步骤4：计算 $3 s$ 与t的和m；	$m = 3 s + t = 23 \times 3 + 29 = 98$ ；
步骤5：取大于或等于m且为10的最小整数倍数n；	$n = 100$ ；
步骤6：计算n与m的差就是校验码X.	$X = 100 - 98 = 2$ ，校验码 $X = 2$ .

【知识运用】请回答下列问题：

(1)、若某商品的条形码为692015246132X ，根据材料计算验证码过程如下：

步骤1：自左向右编号，共13位；

步骤2：求前12位数字中偶数位上的数字之和 $s = 9 + 0 + 5 + 4 + 1 + 2 = 21$ ；

步骤3：求前12位数字中奇数位上的数字之和 $t = 6 + 2 + 1 + 2 + 6 + 0 = 17$ ；

步骤4：计算 $3 s$ 与t的和 $m = 3 s + t =$ ；

步骤5：取大于或等于m且为10的最小整数倍数 $n =$ ；

步骤6：计算n与m的差就是校验码 $X =$ .

(2)、如图②，某商品条形码中的一位数字被墨水污染了，设这位数字为a ，用只含有a的代数式表示

m =

；当

a = 0

时，

m =

，

n =

；当校验码

X = 2

时，

a =

查看试题解析

11. 新定义：如果 $∠ M O N$ 的内部有一条射线 $O P$ 将 $∠ M O N$ 分成的两个角，其中一个角是另一个角的n倍，那么我们称射线 $O P$ 为 $∠ M O N$ 的n倍分线，例如，如图1， $∠ M O P = 4 ∠ N O P$ ，则 $O P$ 为 $∠ M O N$ 的4倍分线． $∠ N O Q = 4 ∠ M O Q$ ，则 $O Q$ 也是 $∠ M O N$ 的4倍分线．

(1)、应用：若 $∠ A O B = 60 °$ ， $O P$ 为 $∠ A O B$ 的二倍分线，且 $∠ B O P > ∠ P O A$ 则 $∠ B O P =$ °；

(2)、如图2，点A ， O ， B在同一条直线上 $O C$ 为直线 $A B$ 上方的一条射线．
①若 $O P$ ， $O Q$ 分别为 $∠ A O C$ 和 $∠ B O C$ 的三倍分线，（ $∠ C O P > ∠ P O A$ ， $∠ C O Q > ∠ Q O B$ ）已知， $∠ A O C = 120 °$ ，则 $∠ P O Q =$ _▲_°；
②在①的条件下，若 $∠ A O C = α$ ， $∠ P O Q$ 的度数是否发生变化？若不发生变化，请写出计算过程；若发生变化，请说明理由．
③如图3，已知 $∠ M O N = 90 °$ ，且 $O M$ ， $O N$ 所在射线恰好是分别为 $∠ A O C$ 和 $∠ B O C$ 的三倍分线，请直接写出 $∠ A O C$ 的度数．

查看试题解析
12. 综合与实践
如图1，用一根质地均匀的 $30 c m$ 的木杆和一些等重量的小物体做下列实验，并记录每一次支点到木杆左右两边挂重物的距离：
①在木杆中间 $15 c m$ 处栓绳作为支点，将木杆吊起来并使左右平衡；
②在木杆两端各悬挂一重物，看左右是否保持平衡；
③在木杆左端小物体下加挂一重物，然后把这两个重物一起向右移动，直至左右平衡；
④在木杆左边继续加挂重物，并重复以上操作和记录如下：
图1 图2
木杆左边挂
重物个数
支点到木杆左边挂
重物的距离
木杆右端挂
重物个数
支点到木杆右端挂
重物的距离
1
$15 c m$
1
$15 c m$
2
$7.5 c m$
1
$15 c m$
3
$5 c m$
1
$15 c m$
……
……
1
$15 c m$
$n$
……
1
$15 c m$

(1)、根据以上的实验记录数据规律，在右端重物个数不变的情况下，若木杆左边悬挂6个重物时，左边重物到支点距离为 $c m$ .

(2)、如图2，在木杆右端挂一重物，支点左边挂 $n$ 个重物，并使左右平衡.设木杆长为 $l c m$ ，支点到木杆左边挂重物处的距离为 $x c m$ ，把 $n$ ， $l$ 作为已知数，列出关于 $x$ 的一元一次方程.

查看试题解析
13. 某实践小组设计宣传牌：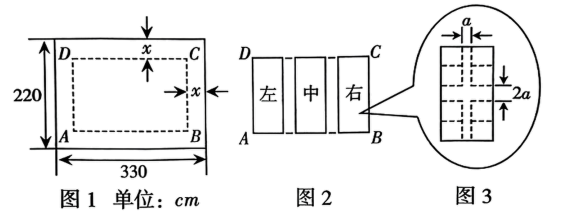
如图1是长方形宣传牌，长 $330 c m$ ，宽 $220 c m$ ，中间可以用来设计的部分是长方形 $A B C D$ ，且 $A B = 1.55 B C$ ．四周空白部分的宽度相等，设四周宽度为 $x c m$ ；
如图2，为了美观，将长方形 $A B C D$ 分割成大小相等的左、中、右三个小长方形栏目，栏目与栏目之间的中缝间距相等；
如图3，每个栏目划出8个小正方形方格，中间有十字间隔，竖行两列中间间隔和横向中间间隔宽度比为 $1 ： 2$ ．

(1)、 $A B =$ $c m$ ， $B C =$ $c m$ （用含 $x$ 的代数式表示）；

(2)、求出图1四周宽度 $x$ 的值；

(3)、求每个栏目的水平宽度；

(4)、求栏目与栏目之间中缝的间距．

查看试题解析

剪去正方形的边长 $/ c m$	1	2	3	4	5	6	7	8	9	10
容积 $/ c m^{3}$	324	512	m	n	500	384	252	128	36	0

剪去正方形的边长/ $c m$	1	2	3	4	5	6	7	8	9	10
容积/ $c m^{3}$	324	512	m	n	500	384	252	128	36	0

木杆左边挂重物个数	支点到木杆左边挂重物的距离	木杆右端挂重物个数	支点到木杆右端挂重物的距离
1	$15 c m$	1	$15 c m$
2	$7.5 c m$	1	$15 c m$
3	$5 c m$	1	$15 c m$
……	……	1	$15 c m$
$n$	……	1	$15 c m$