《旋转、圆与解直角三角形》精选压轴题—广东省（人教版）数学九（上）期末复习

试卷更新日期：2025-01-04 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， E为 $B C$ 延长线上一点，连接 $O D ， O B$ ，若 $O D ∥ B C$ ，且 $O D = B C$ ，则 $∠ B O D$ 的度数是（）．

A、 $65 °$ B、 $115 °$ C、 $130 °$ D、 $120 °$

查看试题解析

二、填空题

2. 如图，在 $△ A B C$ 中， $B C = 4$ ， $∠ A = 45 °$ ，则 $△ A B C$ 面积的最大值为．

查看试题解析
3. 如图，半径为2的扇形AOB的圆心角为120°，点C是弧AB的中点，点D、E是半径OA、OB上的动点，且满足∠DCE＝60°，则图中阴影部分面积等于．

查看试题解析
4. 如图，平面直角坐标系中有一点 $A (4，2)$ ，在以 $M (0，3)$ 为圆心， $2$ 为半径的圆上有一点 $P$ ，将点 $P$ 绕点 $A$ 旋转 $180 °$ 后恰好落在 $x$ 轴上，则点 $P$ 的坐标是．

查看试题解析
5. 如图，量角器的直径与直角三角板 $A B C$ 的斜边 $A C$ 重合，其中量角器0刻度线的端点P与点C重合，射线 $B D$ 从 $B C$ 处出发绕点B沿逆时针方向以每秒2度的速度旋转， $B D$ 与量角器的半圆弧交于点E ，第13秒时，点E在量角器上对应的读数是度．

查看试题解析
6. 如图，在△ABC中，∠C＝90°，AC＝8，AB＝10，D是AC上一点，且CD＝3，E是BC边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为．

查看试题解析
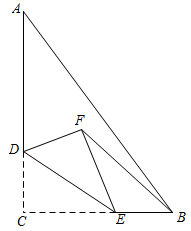7. 如图，矩形 $O A B C$ 起始位置紧贴在坐标轴上，且坐标为 $A (1 ， 0)$ ， $C (0 ， 2)$ ，将矩形 $O A B C$ 绕其右下角的顶点按顺时针方向旋转 $9 0^{°}$ 至图①位置，继续绕右下角的顶点按顺时针方向旋转 $9 0^{°}$ 至图②位置，以此类推，这样连续旋转2022次.则顶点 $A$ 在旋转2023次后的坐标为.

查看试题解析
8. 如图，在 $▱ A B C D$ 中， $A B = \sqrt{3} + 1 ， B C = 2 ， A H ⊥ C D$ ，垂足为 $H ， A H = \sqrt{3}$ ．以点 $A$ 为圆心， $A H$ 长为半径画弧，与 $A B ， A C ， A D$ 分别交于点 $E ， F ， G$ ．若用扇形 $A E F$ 围成一个圆锥的侧面，记这个圆锥底面圆的半径为 $r_{1}$ ；用扇形 $A H G$ 围成另一个圆锥的侧面，记这个圆锥底面圆的半径为 $r_{2}$ ，则 $r_{1} - r_{2} =$ ．（结果保留根号）

查看试题解析
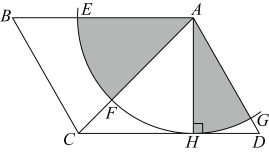9. 如图，在平面直角坐标系中，正六边形 $A B C D E F$ 的中心P在反比例函数 $y = \frac{\sqrt{3}}{x} (x > 0)$ 的图象上，边 $C D$ 在x轴上，点B在y轴上，则该正六边形的边长为。

查看试题解析
10. 如图， $△ A B C$ 中， $∠ B A C = 45 °$ ， $∠ A C B = 75 °$ ，点 $D$ 是 $B C$ 边上一个动点，以 $A D$ 为直径作 $⊙ O$ ，分别交 $A B$ ， $A C$ 于点 $E$ ， $F$ ，若 $A B$ 的长为 $4 \sqrt{3}$ ，弦 $E F$ 长度的最小值为．

查看试题解析

三、解答题

11. 如图，点E为正方形 $A B C D$ 边 $B C$ 上的一点， $C G$ 平分正方形的外角 $∠ D C F$ ，将线段 $A E$ 绕点 $E$ 顺时针旋，点 $A$ 的对应点为点 $H$ ．

(1)、当点 $H$ 落在边 $C D$ 上且 $C E = C H$ 时，求 $∠ A E H$ 的度数；

(2)、当点 $H$ 落在射线 $C G$ 上时，求证： $A E ⊥ E H$ ；

(3)、在（2）的条件下，连接 $A H$ 并与 $C D$ 交于点 $P$ ，连接 $E P$ ，探究 $A P^{2}$ ， $E P^{2}$ 与 $H P^{2}$ 之间的数量关系，并说明理由．

查看试题解析
12. 如图，P是正方形ABCD中一动点，连接PA，PB，PC．

(1)、如图1，若 $B C = P B$ ， $∠ C B P = 30 °$ ，求 $∠ A P C$ 的度数；

(2)、如图2，当 $∠ A P C = 135 °$ 时，求证： $C D = P B$ ；

(3)、如图3，在（2）的条件下，若正方形ABCD的边长为8，Q为BC上一点， $C Q = 2$ ，连接AQ，PQ，求 $△ A P Q$ 面积的最大值．

查看试题解析