精选压轴题—浙教版数学九（上）期末复习

试卷更新日期：2025-01-04 类型：复习试卷

进入出卷网下载

一、二次函数

1. 已知抛物线 $y = a x^{2} + b x + b - a (a < 0)$ ，当 $- 1 \leq x \leq 4$ 时，最大值与最小值的差为 $a^{2}$ ，若将抛物线向左平移4个单位后经过点 $(- 1, 0)$ ，则a的值为（）

A、 $- 8$ B、 $- 9$ C、 $- 10$ D、 $- 11$

查看试题解析
2. 已知二次函数y＝﹣x2+x+6，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新的函数图象（如图所示），当直线y＝﹣x+m与新图象有3个交点时，m的值是（）

A、 $- \frac{25}{4}$ B、﹣2 C、﹣2或3 D、﹣6或﹣2

查看试题解析
3. 如图，学校要在校园内建一个矩形的开心农场，其中一边 $A D$ 是围墙，且 $A D$ 的长不能超过 $28 m$ ，其余三边 $A B$ ， $B C$ ， $C D$ 用 $60 m$ 长的铁质栅栏．有下列结论：
① $A B$ 的长可以为 $15 m$ ；
②当农场 $A B C D$ 面积为 $200 m^{2}$ 时，满足条件的 $A B$ 的长只有一个值；
③农场 $A B C D$ 面积的最大值为 $450 m^{2}$ ；
④若把农场的形状改成半圆形，且直径一侧利用已有围墙，则农场的面积可以超过 $560 m^{2}$ ．
其中，正确结论的是． (只需填序号)

查看试题解析
4. 抛物线y＝ax2+bx+c（a＜0，a、b、c为常数）的部分图象如图所示，其顶点坐标为（-1，n）且与x轴的一个交点在（-3，0）和（-2，0）之间，则下列结论：①a+b+c＜0；②2a-b＝0；③一元二次方程 $a x^{2} + (b + \frac{n}{2}) x + c - \frac{n}{2}$ ＝0的两根为x1、x2，则|x1-x2|＝2；④对于任意实数m ，不等式a（m2-1）+b（m+1）≤0恒成立，其中正确的有（填写序号）

查看试题解析
5. 如图，已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 交 $x$ 轴于 $A (- 2 ， 0) ， B (3 ， 0)$ 两点，交 $y$ 轴于点 $C$ ，直线 $y = k x + m (k < 0)$ 与抛物线交于点 $M ， N$ （点 $M$ 在点 $N$ 的右侧），交 $y$ 轴于点 $P$ ．

(1)、求抛物线的解析式及顶点坐标；

(2)、若 $m = 5$ ，点 $M ， N$ 均在第一象限，且 $△ C M N$ 的面积为3，求 $k$ 的值；

(3)、若 $m = - 3 k$ ，且点 $M$ 在第四象限，直线 $A N$ 交 $y$ 轴于点 $Q$ ，求 $\frac{C P}{C Q}$ 的取值范围.

查看试题解析
6. 如图，抛物线 $y = a x^{2} - \frac{3}{2} x + c (a \neq 0)$ 与x轴交于点A，B，与y轴交于点 $C (0, - 2)$ ， $\tan ∠ A B C = \frac{1}{2}$ ．直线 $x = 1$ 交 $B C$ 于点D，点P是直线 $B C$ 下方抛物线上一动点，连接 $P D$ ．

（1）求此抛物线的解析式；
（2）如图1，连接 $P C$ ，求 $△ P C D$ 面积的最大值及此时点P的坐标；
（3）如图2，连接 $A C$ ，过点P作 $P E ⊥ B C$ 于点E，是否存在点P使以P，D，E三点为顶点的三角形与 $△ A B C$ 相似，若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

二、圆

7. 如图，半径为5的圆中有一个内接矩形 $A B C D ， A B > B C$ ，点 $M$ 是 $\overset{⌢}{A B C}$ 的中点， $M N ⊥ A B$ 于点 $N$ ，若矩形ABCD的面积为30，则线段MN的长为（）.

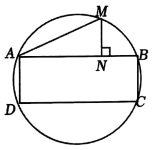A、 $\sqrt{10}$ B、 $\frac{5}{2} \sqrt{2}$ C、 $\frac{\sqrt{70}}{2}$ D、 $2 \sqrt{10}$

查看试题解析
8. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM＝4，BN＝2．若点P是这个网格图形中的格点，连接PM，PN，则所有满足∠MPN＝45°的△PMN中，边PM的长的最大值是（）

A、 $4 \sqrt{2}$ B、6 C、 $2 \sqrt{10}$ D、 $3 \sqrt{5}$

查看试题解析
9. 如图，已知正方形ABCD的边长为4，点E是正方形内部一点，连接BE，CE，且 $∠ A B E = ∠ B C E$ ，点F是AB边上一动点，连接FD，FE，则 $F D + F E$ 的长度最小值为．

查看试题解析
10. 如图，已知 $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E$ ， $O E = B E$ ．点 $P$ 是劣弧 $\overset{⌢}{A D}$ 上任意一点（不与点 $A$ ， $D$ 重合）， $C P$ 交 $A B$ 于点 $M$ ， $A P$ 与 $C D$ 的延长线相交于点 $F$ ，设 $∠ P C D = α$ ．

①则 $∠ F =$ （用含 $α$ 的代数式表示）；
②当 $∠ F = 3 ∠ P C D$ 时，则 $\frac{A M}{B M} =$ ．

查看试题解析
11. 如图1， $A C$ 是平行四边形 $A B C D$ 的一条对角线，且 $A B = A C$ ， $△ A B C$ 的外接圆⊙O与 $C D$ 边交于点E，连结 $A E$ ．

(1)、若 $\tan ∠ A B C = 3$ ， $Δ A E C$ 的面积为 $\frac{81}{5}$ ，求 $⊙ O$ 的半径．

(2)、如图2，过点 $E$ 作 $E H ⊥ A B$ 于 $H$ ，直线 $E H$ 与直线 $B C$ 交于点 $F$ ，若 $C E = \frac{1}{2} H E$ 时，求 $\frac{S_{Δ A B C}}{S_{Δ C E F}}$ 的值．．

查看试题解析
12. 如图⊙O半径为r，锐角△ABC内接于⊙O，连AO并延长交BC于D，过点D作DE⊥AC于E．

(1)、如图1，求证：∠DAB＝∠CDE；

(2)、如图1，若CD＝OA，AB＝6，求DE的长；

(3)、如图2，当∠DAC＝2∠DAB时，BD＝5，DC＝6，求r的值；

(4)、如图3，若AE＝AB＝BD＝1，直接写出AD＋DE的值（用含r的代数式表示）

查看试题解析

三、相似三角形

13. 如图，在 $△ A B C$ 中， $C D$ 平分 $∠ A C B$ ，交 $A B$ 于点D ，过D作 $B C$ 的平行线交 $A C$ 于M ，若 $B C = 3$ ， $A C = 2$ ，则 $D M =$ （　　）

A、 $\frac{5}{6}$ B、 $\frac{6}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
14. 如图，把双曲线 $y = \frac{k}{x} (k > 0 ， x > 0)$ 绕着原点逆时针旋转 $45 °$ 与 $y$ 轴交于点 $B$ ，

(1)、若点B（0，2），则k＝；

(2)、若点A（3，5）在旋转后的曲线上，则k＝．

查看试题解析

四、解直角三角形

15. 如图，在 $Rt$ $△ A P_{1} B$ 中， $A P_{1} = 4$ ， $\tan A = \frac{3}{4}$ ，图中用实线表示的线段与斜边 $A B$ 垂直，用虚线表示的线段都与直角边 $A P_{1}$ 垂直，按照这一规律一直画下去，就会有无数条实线线段，则图中这无数条实线线段的和： $P_{1} Q_{1} + P_{2} Q_{2} + P_{3} Q_{3} + \dots + P_{n} Q_{n} + \dots =$ ．

查看试题解析
16. 魏晋时期，伟大数学家刘徽利用如图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理.已知四边形ABCD、四边形AHFE、四边形DGME均为正方形.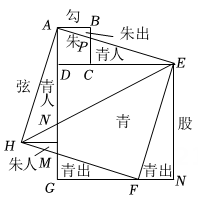

(1)、若AH=13，DE=12，则 $A B =$ ；

(2)、若 $S_{△ A B P} ： S_{△ C E P} = 1 ： 9$ ，则 $t a n ∠ D E H =$ .

查看试题解析

17. 请根据素材，完成任务．

素材一	如图，在 $R t △ A B C$ 中， $C D ⊥ A B$ ，垂足为点D ，若保证 $∠ A C B$ 始终为直角，则点A、B、C在以 $A B$ 为直径的圆上．
素材二	如图，在 $R t △ A B C$ C中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，垂足为点D ，取 $A B$ 的中点O ，连接 $O C$ ，根据“直角三角形斜边上的中线等于斜边的一半”可知 $O C = \frac{1}{2} A B$ ，可得 $O C \geq C D$ ．
素材三	如图，矩形 $A B C D$ 是某实验室侧截面示意图，现需要在室内安装一块长1米的遮光板 $E F$ ，且 $E F ∥ A B$ ，点E到墙 $A B$ 的距离为4米，到地面 $B C$ 的距离为5米．点O为室内光源， $O M$ 、 $O N$ 为光线， $∠ M O N = 40 °$ ，通过调节光源的位置，可以改变背光工作区的大小．若背光工作区 $B M + B N$ 的和最大时，该实验室“可利用比”最高．
任务一	若素材一中的 $A B = 4$ ，求 $C D$ 的最大值．
任务二	若素材二中的 $C D = 6$ ，求 $A B$ 的最小值．
任务三	若任务二中的 $∠ A C B = 90 °$ 改成 $∠ A C B = 60 °$ ，其余条件不变，请直接写出 $A B$ 的最小值．
任务四	若任务二中的 $∠ A C B = 90 °$ ， $C D = 6$ 改成 $∠ A C B = α$ ， $C D = m$ ，请直接写出 $A B$ 的最小值．
任务五	当素材三中的实验室“可利用比”最高，求此时 $B M + B N$ 的值

查看试题解析