浙教版数学八年级上学期期末模拟卷(二)
试卷更新日期:2025-01-04 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,平分 , 点P在上, , , 则点P到的距离是( )
2. 如图,平分 , 点P在上, , , 则点P到的距离是( ) A、4 B、3 C、2 D、13. 为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为 , , 则“技”所在的象限为 ( )
A、4 B、3 C、2 D、13. 为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为 , , 则“技”所在的象限为 ( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式组的解集在数轴上表示正确的是( )A、
A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式组的解集在数轴上表示正确的是( )A、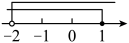 B、
B、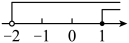 C、
C、 D、
D、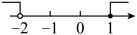 5. 一次函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 在平面直角坐标系中,将点(﹣2,1)沿y轴向上平移1个单位后,得到的点的坐标为( )A、(﹣2,0) B、(﹣2,2) C、(﹣3,1) D、(﹣1,1)7. 关于一次函数 , 下列说法正确的是( )A、图象经过第一、三、四象限 B、图象与y轴交于点 C、函数值y随自变量x的增大而减小 D、当时,8. 如图的三条高相交于点 , 是角平分线,已知 , , 则图中的等腰三角形共有个.
5. 一次函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 在平面直角坐标系中,将点(﹣2,1)沿y轴向上平移1个单位后,得到的点的坐标为( )A、(﹣2,0) B、(﹣2,2) C、(﹣3,1) D、(﹣1,1)7. 关于一次函数 , 下列说法正确的是( )A、图象经过第一、三、四象限 B、图象与y轴交于点 C、函数值y随自变量x的增大而减小 D、当时,8. 如图的三条高相交于点 , 是角平分线,已知 , , 则图中的等腰三角形共有个. A、5 B、6 C、7 D、89. 已知点都在正比例函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、10. 甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距;②甲车的平均速度是 , 乙车的平均速度是;③乙车先出发,先到达B城;④甲车在追上乙车.正确的有( )
A、5 B、6 C、7 D、89. 已知点都在正比例函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、10. 甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距;②甲车的平均速度是 , 乙车的平均速度是;③乙车先出发,先到达B城;④甲车在追上乙车.正确的有( ) A、①② B、①③ C、②④ D、①④
A、①② B、①③ C、②④ D、①④二、填空题(每题3分,共18分)
-
11. 写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式 .12. 关于的不等式组有3个整数解,则实数的取值范围是 .13. 等腰三角形的两边长分别为6和2,则第三边长为 .14. 平面直角坐标系xOy中,已知A(3,0),B(0,3).直线y=kx+b(k , b为常数,且k>0)经过点(1,0),并把△AOB分成两部分,其中靠近原点部分的面积为 , 则k的值为 .15. 如图,四边形AOBC四个顶点的坐标分别是 , , , , 在该平面内找一点P , 使它到四个顶点的距离之和最小,则P点坐标为 .
 16. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
16. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
三、解答题(共8题,共72分)
-
17. 求不等式组的整数解.18. 解不等式组 , 把解集在数轴上表示出来,并写出整数解.
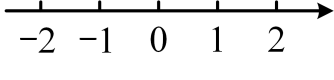 19. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3)
19. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3)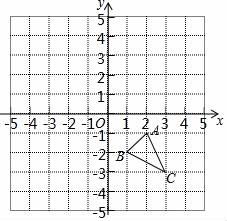
①将△ABC向上平移4个单位长度得到△A1B1C1 , 请画出△A1B1C1;
②请画出与△ABC关于y轴对称的△A2B2C2;
③请写出A1、A2的坐标.
20. 如图,在中, , , , 在射线上有一动点 . (1)、求长;(2)、当为直角三角形时,求值;(3)、当为等腰三角形时,求值.21. 如图,书架宽 , 在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚 , 每本语文书厚 .
(1)、求长;(2)、当为直角三角形时,求值;(3)、当为等腰三角形时,求值.21. 如图,书架宽 , 在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚 , 每本语文书厚 . (1)、数学书和语文书共90本恰好摆满该书架,求书架上数学书和语文书各多少本;(2)、如果书架上已摆放10本语文书,那么数学书最多还可以摆多少本?22. 小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小丽跑步时中间休息了两次.跑步机上C档比B档快40米/分、B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程 (米)与小明跑步时间 (分)的函数关系如图所示.
(1)、数学书和语文书共90本恰好摆满该书架,求书架上数学书和语文书各多少本;(2)、如果书架上已摆放10本语文书,那么数学书最多还可以摆多少本?22. 小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小丽跑步时中间休息了两次.跑步机上C档比B档快40米/分、B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程 (米)与小明跑步时间 (分)的函数关系如图所示.时间
里程分段
速度档
跑步里程
小明
16:00~16:50
不分段
A档
4000米
小丽
16:10~16:50
第一段
B档
1800米
第一次休息
第二段
B档
1200米
第二次休息
第三段
C档
1600米
 (1)、求 , , 各档速度(单位:米/分);(2)、求小丽两次休息时间的总和(单位:分);(3)、小丽第二次休息后,在分钟时两人跑步累计里程相等,求的值.23. 如图,直线y=x+b与x轴交于点A,与y轴交于点B,点P(2,3)在直线y=x+b上,点C是线段OB上一点(不与点O,B重合).
(1)、求 , , 各档速度(单位:米/分);(2)、求小丽两次休息时间的总和(单位:分);(3)、小丽第二次休息后,在分钟时两人跑步累计里程相等,求的值.23. 如图,直线y=x+b与x轴交于点A,与y轴交于点B,点P(2,3)在直线y=x+b上,点C是线段OB上一点(不与点O,B重合). (1)、求点A,B的坐标.(2)、连接PC,将△OPC沿直线PC翻折得到△DPC,点D为点O的对应点,点D在第一象限,且∠OCD=90°.
(1)、求点A,B的坐标.(2)、连接PC,将△OPC沿直线PC翻折得到△DPC,点D为点O的对应点,点D在第一象限,且∠OCD=90°.①求点D的坐标.
②若直线y=x+b与CD交于点E,在y轴上是否存在点Q,使△BEQ是以BE为腰的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
24. 在△ABC中,AB=AC . (1)、AD是BC上的高,AD=AE .
(1)、AD是BC上的高,AD=AE .①如图1,如果∠BAD=30°,则∠EDC= °;
②如图2,、如果∠BAD=40°,则∠EDC= °.
(2)、思考:通过以上两小题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示: .(3)、如图3,如果AD不是BC上的高,AD=AE , 是否仍有上述关系?如有,请你写出来,并说明理由.