阅读理解题—广东省（北师大版）七（上）数学期末复习

试卷更新日期：2025-01-02 类型：复习试卷

进入出卷网下载

一、数轴

1. 阅读下面材料：
①在数轴上，有理数5与-2对应两点间的距离为|5-（-2）|＝7；
②在数轴上，有理数-2与3对应两点之间的距离为|-2-3|＝5；
③在数轴上，有理数-8与-5对应两点之间的距离为|-8-（-5）|＝3；
④在数轴上点A、B分别表示数a，b，则A、B两点之间的距离AB=|a-b|；
回答下列问题：

(1)、①在数轴上表示-2与-5两点间的距离为是，
②在数轴上表示x与3两点间的距离为距离是；
③在数轴上表示x与两点之间的距离为|x+1|

(2)、下面对式子|x+1|+|x-3|进行探究：
①当表示数x的点在-1与3之间移动时，|x+1|+|x-3|的值总是一个固定的值为：。
②要使|x+1|+|x-3|=8，数轴上表示的数x=.

(3)、|x-3|+|x-2|+|x+1|+|x+2|的最小值：.

查看试题解析
2. 【材料阅读】
已知 $(a + 1) x^{3} + 20 x^{2} + (b - 7) x + 5$ 是关于 $x$ 的二次二项式，A，B是如图1数轴上两点，且A，B对应的数分别为a，b.C是线段AB的中点.

(1)、A点对应的数 $a =$ ， $B$ 点对应的数 $b =$ ，点 $C$ 表示的数是；

(2)、若点P、Q分别从点C、B同时出发，以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动，则 $t$ 秒后，点P、Q表示的数分别是、（用含t的代数式表示）；

(3)、在（2）的条件下，若P、Q两点之间的距离为2，求 $t$ 的值.
【方法迁移】
如图2， $∠ A O B = 14 0^{°} ， O C$ 平分 $∠ A O B$ .现有射线OP、OQ分别从OC、OB同时出发，以每秒 $1 5^{°}$ 和每秒 $1 0^{°}$ 的速度绕点 $O$ 顺时针旋转，当OP旋转一周时，这两条射线都停止旋转.问经过几秒后，射线OP、OQ的夹角为 $3 0^{°} ?$
【生活运用】
周末的下午，小明看到钟面显示3点整，此时分针与时针的夹角恰好为 $9 0^{°}$ ，经过多少分钟后，分针与时针的夹角首次变成 $4 5^{°} ?$

查看试题解析
3. 如图

(1)、【材料阅读】
已知 $(a + 1) x^{3} + 20 x^{2} + (b - 7) x + 5$ 是关于x的二次二项式，A，B是如图1数轴上两点，且A，B对应的数分别为a，b．C是线段 $A B$ 的中点．
①A点对应的数 $a =$ ▲ ， B点对应的数 $b =$ ▲ ，点C表示的数是 ▲ ；
②若点P、Q分别从点C、B同时出发，以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动，则t秒后，点P、Q表示的数分别是 ▲ 、 ▲ （用含t的代数式表示）；
③在（2）的条件下，若P、O两点之间的距离为2．求t的值．

(2)、【方法迁移】
如图2， $∠ A O B = 140 °$ ， $O C$ 平分 $∠ A O B$ ．现有射线 $O P$ 、 $O Q$ 分别从 $O C$ 、 $O B$ 同时出发，以每秒 $15 °$ 和每秒 $10 °$ 的速度绕点O顺时针旋转，当 $O P$ 旋转一周时，这两条射线都停止旋转，问经过几秒后，射线 $O P$ 、 $O Q$ 的夹角为 $30 °$ ？

(3)、【生活运用】
周末的下午，小明看到钟面显示3点整，此时分针与时针的夹角恰好为 $90 °$ ，经过多少分钟后，分针与时针的夹角首次变成 $45 °$ ？

查看试题解析

二、一元一次方程

4. 为迎接2024年的到来，滨海学校七（2）班积极筹办元旦联欢活动．班主任李老师在“飞送外卖”上发现了一款由心悦蛋糕店制作的手工泡芙蛋糕．为增添节日氛围，李老师准备订购40个蛋糕送给同学们．根据以下材料，解决问题．

阅读材料

素材1

订购方式	打包费	配送费
“飞送外卖” $A P P$	每个蛋糕收1元	3元/单

注：订单总价（不含打包费和配送费）满50元起送

素材2

蛋糕店专属“心悦红包”：面值10元，订单总价（不含打包费和配送费）满99元可使用．

注：该专属红包仅有1个．

素材3

红包	购买金额
$\times 4$ 个	10元

“飞送外卖”福利：10元购买一组（4个）“神券红包”，面值随机确定．

注：每个“神券红包”面值相等且可以和“心悦红包”同时使用，但每一个订单只允许使用一个“神券红包”．

(1)、若李老师一次性下单购买40个蛋糕，并使用“心悦红包”，且由外卖配送，总花费多少元？

(2)、（列方程解决问题）为了降低费用，李老师购买了一组“神券红包”，先后4次下单共订购40个蛋糕，并将两种红包全部使用，且由外卖配送，所有费用刚好为504元，请计算出每个“神券红包”的面值．

查看试题解析

5. 综合与实践

阅读材料，解答下列问题：

幻方历史悠久，传说最早出现在夏禹时代的“洛书”，如图1．把图1的洛书用今天的数学符号翻译出来，就是一个三阶幻方，如图2，它的每行、每列、每条对角线上的三个数的和都相等．

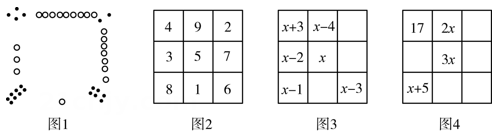(1)、在图2中，每行、每列、每条对角线上三个数的和都是；

(2)、设图3所示的三阶幻方中间的数为x（x为整数），请用含x的代数式将图3幻方补充完整；

(3)、如图4是一个三阶幻方，按方格中已给的信息，求x的值．

查看试题解析

三、最新阅读理解题

6. 请仔细阅读小明的数学日记，并按要求完成相应任务．
x年x月x日晴
整式的加减
我们已经学过整式的加减，知道整式的加减可以归结为合并同类项，而合并同类项实际就是合并同类项的系数．因此，进行整式的加减，关键就是把各同类项的系数进行加减．
今天在课外阅读时我又学习了一种新的解决整式加减问题的方法．具体做法如下：如果把两个整式的各同类项对齐，我们就可以像小学列竖式进行加减法一样，来进行整式的加减运算了．
怎样把同类项对齐呢？其实，只要将参加运算的整式按同一字母进行降幂排列（按同一字母的指数从大到小的顺序排列），凡缺项则留出空位或添零，然后让常数项对齐（即右对齐）即可．
例如：计算 $(x^{3} - 2 x^{2} - 5) + (- 2 x^{2} + x - 1)$ 时，可以用下列竖式计算：
$\begin{array}{r} x^{3} - 2 x^{2} - 5 \\ \underline{+ - 2 x^{2} + x - 1} \\ x^{3} - 4 x^{2} + x - 6 \end{array}$
∴ $(x^{3} - 2 x^{2} - 5) + (- 2 x^{2} + x - 1) = x^{3} - 4 x^{2} + x - 6$ ．
我尝试用上述方法计算： $(2 x^{3} - 3 x^{2} - 5) - (- x^{3} + x + 6)$ ．
$\begin{array}{r} 2 x^{3} - 3 x^{2} - 5 \\ \underline{- - x^{3} + x + 6} \\ 3 x^{3} - 4 x - 11 \end{array}$
∴ $(2 x^{3} - 3 x^{2} - 5) - (- x^{3} + x + 6) = 3 x^{3} - 4 x^{2} - 11$ ．
任务：

(1)、上述小明同学的尝试过程出现了错误，错误的原因是______；

(2)、请帮助小明写出正确的尝试过程．

查看试题解析
7. 【阅读理解】
我们知道： $4 x + 2 x - x = (4 + 2 - 1) x = 5 x$ ，类似的，若我们把 $(a + b)$ 看成一个整体，则有 $4 (a + b) + 2 (a + b)$ $- (a + b) = (4 + 2 - 1) \times (a + b) = 5 (a + b)$ ．这种解决问题的方法渗透了数学中的“整体思想”．“整体思想”是中学数学解题中的一种重要的思想方法，其应用极为广泛．
【方法运用】
（1）把 $(a - b)$ 看成一个整体，则 $3 {(a - b)}^{2} - 7 {(a - b)}^{2} + 2 {(a - b)}^{2} =$ ________；
（2）已知 $x^{2} + 2 y = 5$ ，求代数式 $3 x^{2} + 6 y + 21$ 的值；
（3）当 $x = 2024$ 时，代数式 $a x^{2} - x + 1$ 的值是 $m$ ，则当 $x = - 2024$ 时，求 $a x^{2} - x + 1$ 的值（结果用含 $m$ 的代数式表示）．
【拓展应用】
（4）将一块长方形纸片剪成如图所示的①、②、③、④4个正方形和⑤一个小长方形，设①号正方形的边长为 $x$ ， ②号正方形的边长为 $y$ ．若图中⑤号小长方形的周长为20，试求③号正方形的边长．

查看试题解析

8. 【教材呈现】2024年北师大版七年级上册教材中有以下内容：

【联系拓广】

数轴上任意两点 $A$ ， $B$ 表示的数分别是 $a$ ， $b$ ．

（1）当 $a$ ， $b$ 分别取下列值时，求 $A$ ， $B$ 两点间的距离．

$a = 3$ ， $b = 6$ ； $a = - 3$ ， $b = 6$ ； $a = - 3$ ， $b = - 6$ ．

（2）用 $a$ ， $b$ 表示 $A$ ， $B$ 两点间的距离．

阅读以上内容，回答下面的问题：

【归纳概括】

（1）数轴上表示数3与6的两点之间的距离是________，数轴上表示数 $- 3$ 与6的两点之间的距离是________；

（2）用 $a$ ， $b$ 表示 $A$ ， $B$ 两点之间的距离是________；

【解决问题】

（3） $| x - 3 |$ 的含义是数轴上表示数 $x$ 与________的两点之间的距离， $| x + 4 |$ 的含义是数轴上表示数 $x$ 与________的两点之间的距离；

（4）请你在以下的数轴上表示 $- 4$ 和3两数的位置，当表示数 $x$ 的点在 $- 4$ 与3之间移动时，可以发现 $| x + 4 | + | x - 3 |$ 的值总是一个固定的值，这个值是________；

（5）若动点 $P$ ， $Q$ 分别从 $- 4$ 和3同时出发，沿数轴向左运动，已知点 $P$ 的速度是每秒1个单位长度，点 $Q$ 的速度是每秒2个单位长度，设移动时间为 $t$ 秒（ $t > 0$ ）．

①用含 $t$ 的代数式表示： $t$ 秒时，点 $P$ 表示的数为________，点 $Q$ 表示的数为________；

②当 $t$ 为何值时， $P$ ， $Q$ 两点之间的距离为3？

查看试题解析

9. 我国著名数学家华罗庚说过“数缺形时少直观，形缺数时难入微”，数形结合是解决数学问题的重要思想方法．
材料分析：如图，已知数轴上两点m，n，则两点距离为两数差的绝对值，即 $|m - n|$
如：1到3的距离为两数差的绝对值，即 $|1 - 3| = 2$
x到3的距离为两数差的绝对值，即 $|x - 3|$
根据以上思想，完成下题
如图，已知数轴上两点A，B表示的数分别为 $- 2$ ， 6．

(1)、 $A B$ 两点间的距离为；

(2)、则 $|x + 2|$ 表示的是x到的距离；

(3)、①代数式 $|x + 2| + |x - 6|$ 取最小值时，相应的x的取值范围是；
②当 $a =$ 时，代数式 $|x + a| + |x - 6|$ 的最小值是2；
③代数式 $|x + 2| + |x - 6| + |x - 9|$ 的最小值为；

(4)、点C表示的数是4，点A以2个单位/秒的速度沿着数轴的正方向一直运动，点C同时以1个单位/秒的速度也沿着数轴的正方向运动，但点C到达B 点处立刻返回沿着数轴的负方向运动，设点 A 运动的时间为t，在此过程中存在t使得点A 到点C的距离等于2，请求出t的值．

查看试题解析
10. 阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点 C是点是 $【 A ， B 】$ 的好点．

(1)、如图1，点A 表示的数为 $- 1$ ，点B表示的数为2．表示1的点 C 到点 A 的距离是2，到点B的距离是1，那么点C是 $【 A ， B 】$ 的好点；又如，表示0的点 D 到点 A的距离是1，到点B的距离是2，那么点D $【 A ， B 】$ 的好点，但点D $【 B ， A 】$ 的好点．（请在横线上填是或不是）
知识运用：如图2，M、N为数轴上两点，点M所表示的数为 $- 2$ ，点N所表示的数为4．

(2)、求 $【 M ， N 】$ 的好点所表示的数；

(3)、如图3， A、B为数轴上两点，点A 所表示的数为 $- 20$ ，点 B所表示的数为40．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止，当经过多少秒时，P、A和B中恰有一个点为其余两点的好点？

查看试题解析
11. 【阅读材料】我们在数学的学习过程中要接触到“数”和“形”，它们在一定条件下可以相互转化，这样的联系称为数形结合．数形结合是一种重要的数学思想方法，有着广泛的应用，在中学数学阶段，数形结合应用大致分为两种情形：借助数的精确性来阐明形的某些属性，或者借助形的几何直观来阐明数之间某种关系．
我们学习过的绝对值知识从形的角度来解释就是： $|a|$ 表示在数轴上数a到原点的距离．借助绝对值的形的解释，我们就可以得到 $|a| \geq 0$ ．又比如 $|7 - 3|$ 从数的角度来解释：表示7与3差的绝对值；从形的角度来解释：7与3两个数在数轴上所对应的两点之间的距离．
【分析应用】如图1，A、B是数轴上两点（A在B的左侧），A表示的数是 $- 3$ ．动点M从点A出发，以每秒3个单位的速度沿数轴向右匀速运动．
图1
                       备用图

(1)、B点表示的数是              ， A和B两点之间的距离为             ；

(2)、① $|5 - 2|$ 从形的角度来解释：5与             两数在数轴上所对应的两点之间的距离；
②数轴上表示数a和 $- 3$ 的两点之间的距离表示为             ；
③当a为             时， $|a + 3| + |a - 2| = 13$ ．

(3)、若动点M在A和B两点之间运动，其对应数的为 $x$ ，化简： $|x + 3| - 2 |x - 4|$ （写出化简过程）．

(4)、若动点N从点O出发，以每秒1个单位长度的速度沿数轴向右匀速运动，若M、N同时出发，问点M运动多少秒时，M、N相距1个单位长度？

查看试题解析