浙教版数学七年级上学期期末模拟卷（一）

试卷更新日期：2025-01-02 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列结论中正确的是（）

A、单项式 $\frac{π x^{2} y}{4}$ 的系数是 $\frac{1}{4}$ ，次数是4 B、 $\frac{x y}{3} - 1$ 是多项式 C、单项式m的次数是1，无系数 D、多项式 $x + x^{2} y^{2} + 3 y$ 是二次三项式

查看试题解析
2. 我国近年来大力推进国家教育数字化战略行动，截至2024年6月上旬，上线慕课数量超过7.8万门，学习人次达1290000000，建设和应用规模居世界第一.用科学记数法将数据1290000000表示为（）

A、 $1.29 \times 1 0^{8}$ B、 $12.9 \times 1 0^{8}$ C、 $1.29 \times 1 0^{9}$ D、 $129 \times 1 0^{7}$

查看试题解析
3. 下列运算中，正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $2 a^{2} + 3 a^{2} = 5 a^{2}$ C、 $3 a^{2} - 2 a^{2} = 1$ D、 $2 a^{2} b - 2 a b^{2} = 0$

查看试题解析
4. 估计 $\sqrt{5}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 下列计算，正确的是（）

A、 $2 \sqrt{3} + 2 \sqrt{2} = 2 \sqrt{5}$ B、 $2 \sqrt{3} \times 2 \sqrt{2} = 2 \sqrt{6}$ C、 $\sqrt{8} \div \sqrt{2} = 2$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
6. 若代数式3a+1的值与3（a+1）的值互为相反数，则a的值为（）

A、 $- \frac{2}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图，AB=18，C为AB 的中点，点D 在线段AC上，且AD：CB=1：3，则 DB 的长为（）

A、8 B、10 C、12 D、15

查看试题解析
8. 小琪在解关于x的方程 $\frac{x + 4}{3} - \frac{x + k}{4} = 2$ 去分母时，等号右边的2忘记乘12，她求得的解为x=-1，则k的值为（）

A、 $\frac{13}{3}$ B、2 C、- 1 D、- 3

查看试题解析
9. 如图，点 $O$ 在直线 $A B$ 上，射线 $O C$ ， $O D$ 在直线 $A B$ 的同一侧（其中 $0 ° < ∠ A O C < 90 °$ ， $0 ° < ∠ B O D < 90 °$ ），射线 $O E$ 平分 $∠ A O C$ ，射线 $O F$ 平分 $∠ B O D$ ．若 $∠ E O D$ 和 $∠ C O F$ 互补，则（）

A、 $∠ A O C = 60 °$ B、 $∠ C O F = 90 °$ C、 $∠ C O D = 60 °$ D、 $∠ A O D = 120 °$

查看试题解析
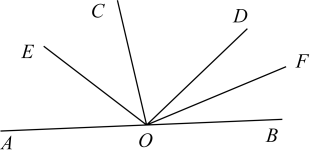10. 程大位是我国明朝商人，珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法.书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁.意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人?若设大和尚有x人，则列出的方程正确的是（）

A、 $3 x + \frac{x}{3} = 100$ B、 $\frac{x}{3} + 3 (100 - x) = 100$ C、 $3 x + \frac{100 - x}{3} = 100$ D、 $\frac{x}{3} + 100 - 3 x = 100$

查看试题解析

二、填空题（每题3分，共18分）

11. $23 ° 1 4^{'} 2 4^{″}$ 化为用度表示是．

查看试题解析
12. 若规定 $a △ b = \frac{a + 2 b}{2} ，$ 则方程 $3 △ | x | = 4$ 的解 $x =$ .

查看试题解析
13. 已知有理数 $x$ ， $y$ 满足： $| x - 2 | = 3$ ， ${(y + 1)}^{2} = 4$ 且 $| x + y | = x + y$ ，则 $x - y =$ ．

查看试题解析
14. 如图，在天平上放若干个苹果和香蕉（每个苹果和每个香蕉的质量分别相等），其中①②的天平保持平衡，现要使③中的天平也保持平衡，需要在天平右盘中放入砝码克.

查看试题解析
15. 如图，∠BOC=2∠AOC，OD 平分∠AOB，OE 平分∠AOC，则∠DOE 与∠AOB 的数量关系为.

查看试题解析
16. 在外地打工的赵先生下了火车，为尽快与家人团聚，他打算乘坐市内出租车.市客运公司规定：起步价为10元（不超过3千米收10元），超过3千米的部分每千米要加收一定的费用.赵先生上车时看了一下里程表，车到家门口时又看了一下里程表.
上车时里程表
起步价（元）
10.00
超过3千米
每千米加收（元）
×××
总价（元）
10.00
时间
17：05
下车时里程表
起步价（元）
10.00
超过3千米
每千米加收（元）
×××
总价（元）
55.00
时间
17：25
已知火车站到他家的路程为18千米，则行程超过3千米的部分每千米加收元.

查看试题解析

三、解答题（共8题，共72分）

17. 计算：

(1)、 $\sqrt[3]{- 8} + |\sqrt{3} - 3| + \sqrt{{(- 3)}^{2}} - (- \sqrt{3})$ ．

(2)、 $- 1^{4} - (\frac{1}{2} - 1) \times [- 2^{3} + {(- 3)}^{2}]$ ．

查看试题解析
18. 解一元一次方程：

(1)、 $3 - 2 x = 5 x + 10$ ；

(2)、 $\frac{x - 1}{3} = 1 - \frac{3 x + 1}{6}$ ．

查看试题解析
19. 先化简，再求值： $2 x^{2} + 4 y^{2} + (2 y^{2} - 3 x^{2}) - 2 (y^{2} - 2 x^{2})$ ，其中x＝-1，y＝ $\frac{1}{2}$ ．

查看试题解析
20. 先化简，再求值： $4 x y - 2 (\frac{3}{2} x^{2} - 2 y^{2}) + 3 (x^{2} - 2 x y)$ ，（其中 $x = 2$ ， $y = 1$ ）

查看试题解析
21. 若方程 $\frac{1 - 2 x}{6} + \frac{x + 1}{3} = 1 - \frac{2 x + 1}{4}$ 与关于x的方程 $x + \frac{6 x - a}{3} = \frac{a}{6} - 3 x$ 的解相同，求字母a 的值.

查看试题解析
22. 列一元一次方程求解。
某中学学生步行到距离学校20千米的郊外旅行。女学生组成前队，步行速度为4千米/小时，男学生组成后队，速度为6 千米/小时。前队出发1小时后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回联络，他骑车的速度为10千米/小时。

(1)、后队追上前队需要多长时间? 这段时间联络员走的路程是多少?

(2)、两队何时相距2千米?

查看试题解析
23.

(1)、如图，∠AOB = 90°，∠BOC = 30°，OM 平分∠AOB，ON 平分∠BOC，求∠MON 的度数.

(2)、若（1）中的∠AOB=α，其他条件不变，求∠MON 的度数.

(3)、若（1）中的∠BOC=β（β为锐角），其他条件不变，求∠MON 的度数.

(4)、从（1）（2）（3）的结果中你能发现什么规律?

查看试题解析
24.

(1)、【问题探究】
如图，点C，D 均在线段AB 上且点C 在点 D 左侧，若AC=BD，CD=6 cm，AB=9 cm，则线段AC 的长为 cm。

(2)、【方法迁移】
已知点C，D 均在线段AB 上且点C 在点D 左侧，若AC=BD，CD=a( cm)，AB=b( cm)(b>a)，则线段AC 的长为 cm(用含a，b 的代数式表示)。

(3)、【学以致用】
已知七年级某班共有m人，在本班参加拓展课报名统计时发现，选择围棋课的人数是n(n<m)，其中未参加围棋课的男生人数是参加围棋课男生人数的一半，参加围棋课的女生人数是女生总人数的 $\frac{2}{3}$ ，求m与n 的数量关系。小聪同学在思考这个问题时联想到了上面的几何问题，并将这个实际问题转化为几何模型来解决，请你建立这个几何模型并求解。

查看试题解析

上车时里程表
起步价（元）	10.00
超过3千米每千米加收（元）	×××
总价（元）	10.00
时间	17：05

下车时里程表
起步价（元）	10.00
超过3千米每千米加收（元）	×××
总价（元）	55.00
时间	17：25