浙教版数学八年级上学期期末模拟卷（一）

试卷更新日期：2025-01-02 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是( )

A、 B、 C、 D、

查看试题解析
2. 若等腰三角形的两边长分别是3cm和5cm，则这个等腰三角形的周长是（）

A、8cm B、13cm C、8cm或13cm D、11cm或13cm

查看试题解析
3. 如图，在 $R t △ A B C$ 中，D是 $A C$ 的中点， $∠ B D C = 60 °$ ， $A C = 6$ ，则 $B C$ 的长是（）

A、3 B、6 C、 $\sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
4. 下列不等式中，与 $- x > 1$ 组成的不等式组无解的是（）

A、 $x > 2$ B、 $x < 0$ C、 $x < - 2$ D、 $x > - 3$

查看试题解析
5. 在平面直角坐标系中，将点 $P (3, 5)$ 向上平移2个单位长度后得到点 $P^{^{'}}$ 的坐标为（）

A、 $(1, 5)$ B、 $(5, 5)$ C、(3，3) D、(3，7)

查看试题解析
6. 点P（a ， ﹣3）关于原点对称的点是P^'（2，b），则a+b的值是（　　）

A、1 B、﹣1 C、﹣5 D、5

查看试题解析
7. 如图，一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体，向水槽匀速注水。下列图象能大致反映水槽中水的深度h与注水时间t的函数关系的是（）

A、 B、 C、 D、

查看试题解析
8. 在同一坐标系中，函数 y= mx与函数 y=x-m的图象可能是( )

A、 B、 C、 D、

查看试题解析
9. 已知不等式 $k x + b < 0$ 的解集是 $x < 2$ ，则一次函数 $y = k x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 甲乙两地相距a千米，小亮8：00乘慢车从甲地去乙地，10分钟后小莹乘快车从乙地赶往甲地．两人分别距甲地的距离y（千米）与两人行驶时刻t（×时×分）的函数图象如图所示，则小亮与小莹相遇的时刻为（）

A、8：28 B、8：30 C、8：32 D、8：35

查看试题解析

二、填空题（每题3分，共18分

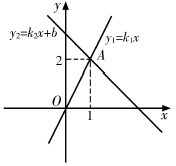
11. 一次函数 $y = (3 m + 1) x - 2$ 的值随 $x$ 的增大而增大，请写出一个满足条件的 $m$ 的值．

查看试题解析
12. 点P（a²+1，﹣3）在第象限．

查看试题解析
13. 如图，直线y₁=k₁x与直线y₂=k₂x+b交于点A（1，2）．当y₁<y₂时，x的取值范围是．

查看试题解析
14. 若关于 $x$ 的不等式组 ${\begin{array}{l} 3 (x - 1) > x - 6 \\ 8 - 2 x + 2 a \geq 0 \end{array}$ 有三个整数解，则实数 $a$ 的取值范围为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ D C E = 40 °$ ， $A E = A C$ ， $B C = B D$ ，则 $∠ A C B$ 的度数为

查看试题解析
16. 已知王强家、体育场、学校在同一直线上，下面的图像反映的过程是：某天早晨，王强从家跑步去体育场锻炼，锻炼结束后，步行回家吃早餐，饭后骑自行车到学校．图中 $x$ 表示时间， $y$ 表示王强离家的距离．则下列结论正确的是．（填写所有正确结论的序号）
①体育场离王强家 $2.5 k m$
②王强在体育场锻炼了 $30 m i n$
③王强吃早餐用了 $20 m i n$
④王强骑自行车的平均速度是 $0.2 k m / m i n$

查看试题解析

三、解答题（共9题，共72分）

17. 解不等式组： $\{\begin{array}{l} 4 x ＞ 2 (x - 1) ① \\ \frac{x + 2}{2} ＜ \frac{x + 5}{3} ② \end{array}$ ，并写出它的所有整数解．

查看试题解析
18. 解不等式组 ${\begin{cases} 2 x - 1 ＜ - 9 ， \\ 1 - x \geq \frac{2 + x}{3} . \end{cases}$

查看试题解析
19. 已知：如图，点M在 $∠ A O B$ 的边 $O A$ 上．

求作：射线 $M N$ ，使 $M N ∥ O B$ ．且点N在 $∠ A O B$ 的平分线上．

作法：①以点O为圆心，适当长为半径画弧，分别交射线 $O A$ ， $O B$ 于点C，D．

②分别以点C，D为圆心．大于 $\frac{1}{2} C D$ 长为半径画弧，两弧在 $∠ A O B$ 的内部相交于点P．

③画射线 $O P$ ．

④以点M为圆心， $O M$ 长为半径画弧，交射线 $O P$ 于点N．

⑤画射线 $M N$ ．

射线 $M N$ 即为所求．

(1)、用尺规作图，依作法补全图形(保留作图痕迹)；

(2)、根据以上作图过程，完成下面的证明．
证明：∵ $O P$ 平分 $∠ A O B$ ．

∴ $∠ A O N =$ ，

∵ $O M = M N$ ，

∴ $∠ A O N =$ ，（）．(括号内填写推理依据)

∴ $∠ B O N = ∠ O N M$ ．

∴ $M N ∥ O B$ ．（）．(填写推理依据)

查看试题解析
20. 如图，点 $C$ 在线段AD上， $A B = A D, ∠ B = ∠ D, B C = D E$ .

(1)、求证： $△ A B C ≅ △ A D E$ ：

(2)、若 $∠ B A C = 6 0^{°}$ ，求 $∠ A C E$ 的度数.

查看试题解析
21. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ， $∠ E D F = ∠ C$ ．

(1)、求证： $∠ B D F = ∠ A$ ；

(2)、若 $∠ A = 45 °$ ， $D F$ 平分 $∠ B D E$ ，请直接写出 $△ A B C$ 的形状．

查看试题解析
22. 为增强学生的劳动意识，养成劳动的习惯和品质，某校组织学生参加劳动实践．经学校与劳动基地联系，计划组织学生参加种植甲、乙两种作物．如果种植3亩甲作物和2亩乙作物需要27名学生，种植2亩甲作物和2亩乙作物需要22名学生．
根据以上信息，解答下列问题：

(1)、种植1亩甲作物和1亩乙作物分别需要多少名学生？

(2)、种植甲、乙两种作物共10亩，所需学生人数不超过55人，至少种植甲作物多少亩？

查看试题解析
23. 如图，在直角坐标系中，点 $A (2 ， m)$ 在直线 $y = 2 x - \frac{5}{2}$ 上，过点 $A$ 的直线交 $y$ 轴于点 $B (0 ， 3)$ .

(1)、求m的值和直线AB的函数表达式。

(2)、若点 $P (t ， y_{1})$ 在线段AB上，点 $Q (t - 1 ， y_{2})$ 在直线 $y = 2 x - \frac{5}{2}$ 上，求 $y_{1} - y_{2}$ 的最大值.

查看试题解析
24. 一条公路上依次有A、B、C三地，甲车从A地出发，沿公路经B地到C地，乙车从C地出发，沿公路驶向B地．甲、乙两车同时出发，匀速行驶，乙车比甲车早 $\frac{2}{7}$ 小时到达目的地．甲、乙两车之间的路程y km与两车行驶时间xh的函数关系如图所示，请结合图象信息，解答下列问题：

(1)、甲车行驶的速度是km/h ，并在图中括号内填上正确的数；

(2)、求图中线段EF所在直线的函数解析式（不要求写出自变量的取值范围）；

(3)、请直接写出两车出发多少小时，乙车距B地的路程是甲车距B地路程的3倍．

查看试题解析