综合与实践题—广东省(北师版)八(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、期末实践与探究题
-
1. [问题情境]
在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如题24图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D.

[探索发现]
(1)、当∠A=60°时,求证:∠CBD=∠A.(2)、”快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系.①当∠A=40°时,∠CBD=度;
②当∠A=x°时,∠CBD=度(用含x的代数式表示).
(3)、[操作探究]”智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变.请写出它们的关系,并说明理由.
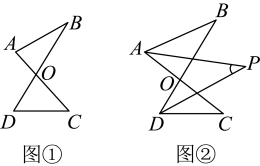
2. (1)、已知:如图①的图形我们把它称为“8字形”,试说明: .(2)、如图②,分别平分 , 若 , 求的度数.(3)、如图③,直线平分 , 平分的外角 , 猜想与的数量关系并证明.3. 我们学习了平移、旋转、轴对称等图形变换,这些图形变换不仅可以应用到精美的图案设计上,还可以解决生活实际问题.
(1)、已知:如图①的图形我们把它称为“8字形”,试说明: .(2)、如图②,分别平分 , 若 , 求的度数.(3)、如图③,直线平分 , 平分的外角 , 猜想与的数量关系并证明.3. 我们学习了平移、旋转、轴对称等图形变换,这些图形变换不仅可以应用到精美的图案设计上,还可以解决生活实际问题. (1)、【图案设计】
(1)、【图案设计】如图1,在平面直角坐标系中, , , .
作出关于轴的对称图形 , 并标注出点 , , ;
(2)、【拓展应用】如图1,点是轴上一动点,并且满足的值最小,请在图中找出点的位置(保留作图痕迹),并直接写出的最小值为.
(3)、【实际应用】如图2,某地有一块三角形空地 , 已知 , 是内一点,连接后测得米,现当地政府欲在三角形空地中修一个三角形花坛 , 点 , 分别是 , 边上的任意一点(不与各边顶点重合),请问的周长最少约多少米?(保留整数)( , )
4. 【问题呈现】如图①,已知线段 , 相交于点 , 连结 , , 我们把形如这样的图形称为“字型”.
 (1)、证明: .(2)、【问题探究】
(1)、证明: .(2)、【问题探究】继续探究,如图②,、分别平分、 , 、交于点 , 求与、之间的数量关系.为了研究这一问题,尝试代入、的值求的值,得到下面几组对应值:
表中 , 猜想得到与、的数量关系为;
(3)、证明()中猜想得到的与、的数量关系;(单位:度)
(单位:度)
(单位:度)
5. 通过一次函数的学习,我们学会了列表、描点、连线的方法来画出函数图象并结合函数图象研究函数性质小明想应用这个方法来探究函数的性质下面是他的探究过程,请你补充完整: (1)、列表:
(1)、列表:直接填空: .
(2)、描点并画出该函数的图象.(3)、观察的图象,类比一次函数,请写出该函数的两条性质:;
.
(4)、在平面直角坐标系中,我们将横、纵坐标均为整数的点称为整点则该函数图象与直线围成的区域内不包括边界整点的个数为 .6. 刻漏是人类最早制造的不完全依赖天象、相对独立运行的计时仪器.刻漏以水等液体(也有少数例外,如水银或沙等)为工作物质,根据流水的量与流逝时间的对应关系,通过漏壶中的水量变化来度量时间的.我国使用刻漏的时间非常早,最早可追溯到中国历史上第一个王朝—夏朝(大约公元前2070年),约在汉武帝时期发明了浮箭漏.如图所示为单级浮箭漏示意图.某兴趣小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每1小时记录一次箭尺读数,得到如表:
供水时间x(小时)
0
1
2
3
4
箭尺读数y(厘米)
6
12
18
24
30
【探索发现】
(1)在所给的平面直角坐标系中,描出以供水时间x为横坐标,箭尺读数y为纵坐标的各点.
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
(3)供水时间达到10小时时,箭尺的读数为多少厘米?
(4)如果本次实验记录的开始时间是上午 , 那当箭尺读数为96厘米时是几点钟?(箭尺最大读数为100厘米)
7. 小明在学习一次函数后,对形如y=k(x-m)+n(其中k,m,n为常数,且k≠0) 的一次函 数图象和性质进行了探究,过程如下: (1)、[特例探究]
(1)、[特例探究]如图所示,小明分别画出了函数y=(x-2)+1,y=-(x-2)+1,y=2(x-2)+1的图象(网格中每个小方格边长为1).通过对上述几个函数图象的观察、思考,发现y=k(x-2)+1(k为常数,且k≠0) 的图象一定会经过的点的坐标是 ;
(2)、[深入探究]归纳:函数y=k(x-m)+n (其中k、m、n为常数,且k≠0)的图象上定会经过的点的坐标是 ;(用含m,n的字母表示)
(3)、[实践运用]已知一次函数y=k(x+2)+3(k为常数,且k≠0)的图象一定会经过点N,且与y轴相交于点M,点O为坐标原点,若AOMN的面积为4,求k的值.
8. 小颖根据学习函数的经验,想对函数的图象和性质进行探究.通过查阅资料,小颖了解到该函数的含义是:当时,;当时, , 请你帮她继续完成探究. (1)、在自变量的取值范围内,与y的几组对应值如下表:其中 .
(1)、在自变量的取值范围内,与y的几组对应值如下表:其中 .0
1
2
3
4
5
6
7
…
y
2
1
0
1
2
3
5
…
(2)、在平面直角坐标系中,已知函数y的部分图象如图所示,请补全函数y的图象,并根据图象写出该函数的一条性质: ▲ ;(3)、已知函数的图象与函数y的图像关于y轴对称.①请在图中画出函数的图象;
②把函数与函数y的图像合称为图象 , 若点与点均在图象上,则a的值为 ▲ .
9. 【定义】如图1,在同一平面内,点在线段所在直线的两侧,若 , 且 , 则称点与是线段的等垂对称点。 (1)、【理解】如图2,在正方形网格中,点均在格点上,连接 , 则下列各组点是线段的等垂对称点的是;(填序号)
(1)、【理解】如图2,在正方形网格中,点均在格点上,连接 , 则下列各组点是线段的等垂对称点的是;(填序号)①点与点 ②点与点 ③点与点 ④点与点
(2)、如图3,在四边形中,是边上一点,点与是线段的等垂对称点,①求证:;
②若平分 , 试探究与之间的数量关系,并说明理由。
(3)、【拓展】如图4,已知直线与坐标轴交于点 , 直线与坐标轴交于点 , 当点中恰有两点是线段的等垂对称点,且时,请直接写出线段的长。10. 综合实践:素材
如图①所示,、两地相距720千米,地位于、两地之间.高铁从地出发经地匀速驶向地,高铁从地出发经地驶往地.

素材
月日高铁时刻表
站名
到时
发时
停留
A站
——
09:00
——
C站
11:00
11:10
10分
B站
12:10
——
——

1月10日高铁G235时刻表
站名
到时
发时
停留
B站
——
09:00
——
C站
10:30
10:35
5分
A站
12:35
——
——
问题解决
任务1
收集信息
a的值为______,b的值为______,高铁G234在行驶过程中速度是______km/min.
任务2
建立一次函数模型
根据图②求高铁G235由C站往A站行驶过程中距离C站的路程y(km)与行驶时间x(min)之间的函数表达式.
任务3
解决问题
求出1月10日G234、G235两列高铁在相遇后两车之间距离不超过200km的当日时刻范围.
11. 在数学小组探究学习中,小华与他的小组成员遇到这样一道题:已知 , 求的值.他们是这样解答的:即
请你根据小华小组的解题方法和过程,解决以下问题:
(1)、.(2)、化简.(3)、若 , 求的值.12. 如下图,某学校计划在校内一道路旁建造超市,将地图简化,如图1所示,宿舍楼与校内道路的距离为50米,教学楼与校内道路的距离为160米,米,现要在校内道路旁建造一超市.


 (1)、请在图1中画出点(点在道路上,道路宽度忽略不记),使学生从宿舍楼走到超市 , 再走到教学楼所走路程最短,并求出最短路程.(2)、如图2所示,若宿舍楼和教学楼之间有一面70米长的校园文化墙 , 文化墙垂直于校内道路 , 到校内道路的距离为40米,米,米,现在依然要求学生从宿舍楼走到超市 , 再走到教学楼所走路程最短.
(1)、请在图1中画出点(点在道路上,道路宽度忽略不记),使学生从宿舍楼走到超市 , 再走到教学楼所走路程最短,并求出最短路程.(2)、如图2所示,若宿舍楼和教学楼之间有一面70米长的校园文化墙 , 文化墙垂直于校内道路 , 到校内道路的距离为40米,米,米,现在依然要求学生从宿舍楼走到超市 , 再走到教学楼所走路程最短.①众所周知,“两点之间,线段最短”,但由于文化墙这个障碍物的存在,需要研究两点之间不同折线长度的大小关系,他认为 , 并进行了证明,请你将下述证明过程补充完整:
证明:如图4,延长交于点 ,
,
又 , ▲ ,
②如图5,延长交校内道路于点 , 过作于点 , 是上右侧的一点,利用①中证明的结论,可判断超市的位置应位于 ▲ (从以下四个选项中选择).
A.左侧B.线段上C.线段上(不含点)D.右侧
③请在图6中画出超市的位置,并求出最短路程.
13. 如图 (1)、【问题背景】太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线OB、OC等反射以后沿着与POQ平行的方向射出.
(1)、【问题背景】太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点O照射到抛物线上的光线OB、OC等反射以后沿着与POQ平行的方向射出.若 , 则;
(2)、【类比发现】如图1、2、3,把呈抛物线的曲面镜改成两平面镜PA、PC,且 , 点O在的角平分线PQ上,从点O照射到平面镜PA上的光线OB,经过平面镜PA与PC反射若干次.某创新兴趣小组的成员发现,当光线OB和平面镜PA的夹角(记为)与反射的总次数n(n是正整数)满足某种数量关系时,反射光线可以沿着与POQ平行的方向射出.①当光线OB经过平面镜PA与PC反射n次后,沿POQ平行的方向射出,根据反射的次数,填写下表中角的度数:
经平面镜反射的总次数n
1次
2次
3次
②当光线OB经过平面镜PA与PC反射n次后,沿POQ平行的方向射出,则与n的数量关系为;
(3)、【拓展延伸】若两平面镜PA、PC的夹角 , 其他条件不变.当光线OB经平面镜PA与PC反射n次后,沿着与POQ平行的方向射出时,请直接写出、与n之间的数量关系为 .二、最新实践与探究题
-
14. 小明同学根据函数的学习经验,对函数y=|x﹣2|+|x+4|进行了探究,下面是他的探究过程:
(1)已知当x=﹣4时,|x+4|=0;当x=2时,|x﹣2|=0,化简:
①当x<﹣4时,y= ;
②当﹣4≤x≤2时,y= ;
③当x>2时,y= .
(2)在平面直角坐标系中画出y=|x﹣2|+|x+4|的图象,根据图象写出该函数的一条性质: .
(3)根据上面的探究解决下面问题:
已知P(a,0)是x轴上一动点,A(﹣4,6),B(2,6),则AP+BP的最小值是 .
 15. 问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:
15. 问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:其中三角形边长分别为a,b,c,三角形的面积为S.
(1)、利用材料1解决下面的问题:当时,求这个三角形的面积?(2)、利用材料2解决下面的问题:已知三条边的长度分别是 , 记的周长为.①当时,请直接写出中最长边的长度;
②若为整数,当取得最大值时,请用秦九韶公式求出的面积.
16. 【项目式学习】在圆柱表面,蚂蚁怎么爬行路径最短? (π取3)素材1:如图1,圆柱体的高AC为12cm,底面直径BC为6cm,在圆柱下底圆周上的A点有一只蚂蚁,它想吃到上底面圆周上与A 点对应的B 点处的食物.
若蚂蚁沿图1中的折线A→C→B爬行的最短路径记为“路线一”,此时最短路程是 12+6=18cm. 将圆柱沿着AC将侧面展开得到图2,请在图2中画出蚂蚁爬行的最短路径记为“路线二”,此时最短路程是____ cm; 比较可知:蚂蚁爬行的最短路径是路线____(用“一”或“二”填空).


素材2:如图3所示的实践活动器材包括:底面直径为6cm,高为10cm的圆柱、橡皮筋、细线(借助细线来反映爬行的路线)、直尺,通过调节橡皮筋的位置达到改变圆柱的高度的目的.
(1)、 两种路线路程的长度如表所示(单位:cm):圆柱高度
沿路线一路程x
沿路线二路程y
比较x与y的大小
5
11
x>y
4
10
x>y
3
a
3
b
(2)、填空:表格中a的值是;表格中b表示的大小关系是;(3)、经历上述探究后,请你思考:若圆柱的半径为r,圆柱的高为h. 在r不变的情况下,当圆柱半径为r与圆柱的高度h存在怎样的数量关系时,蚂蚁在圆柱表面的两种爬行路线的路程相等?17. 【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的. 随之,新能源汽车电池的充电状态和行驶过程中电量的消耗成为关注的焦点。【实验操作】
为了解汽车电池需要多久能充满,以及充满电量状态下汽车的最大行驶里程,八年级某综合实践小组设计两组实验
实验一:探究电池充电状态下汽车仪表盘显示电量y1(%)与时间t(小时)的关系,数据记录如表1.
表1:电池充电状态
时间t(小时)
0.5
1
1.5
2
电量y1(%)
25
50
75
100
实验二:探究充满电量状态下汽车行驶过程中仪表盘显示电量y2(%)与行驶里程s(千米)的关系,数据记录如表2.
表 2: 汽车行驶过程
已行驶里程s(千米)
0
80
100
140
电量y2 (%)
100
60
50
30
(1)、任务一:由表1 可知:每隔0.5小时电池电量增加;(2)、【建立模型】任务二:结合表1、表2的数据,实验小组发现y1关于t为正比例函数模型,y2关于s为一次函数模型,请求出y1关于t的函数表达式及y2关于s的函数表达式;
(3)、【解决问题】任务三:某电动汽车在充满电量的状态下出发,前往距离出发点250千米处的目的地,若电动车平均每小时行驶40千米,行驶3小时后,在途中的服务区充电,一次性充电若干时间后汽车以原速度继续行驶,若要保证司机在最短的时间快速到达目的地,则至少要在服务区充电多长时间?
18. 某校八年级开展了《为家人选择合适的手机资费套餐》项目学习.以下是小露同学帮奶奶选择手机资费套餐的活动报告,请你将其补充完整.为家人选择合适的手机资费套餐活动报告
一、收集信息收集并整理奶奶近六个月的话费账单,发现她使用流量和短信极少,故忽略流量和短信情况进行研究.根据她的月平均通话时间筛选出两款比较适合她的手机资费套餐.
甲套餐:月租费8元,送30分钟通话时间,超出的部分按每分钟0.25元计;
乙套餐:月租费29元,通话费按每分钟0.1元计.
二、建立模型

1.发现每月的手机资费y(元)与通话时间x(分)之间存在函数关系,y与x之间的关系式为:?甲= , ?乙=(x≥0).
2.为了直观比较,在同一坐标系内画出两个函数的图象(如图).图中A点表示的实际意义是 .
3.解决问题根据图象可知:如果从节省费用的角度考虑,当通话时间时,选择甲套餐更合适;当通话时间时,选择乙套餐更合适.
19. 某校八年级开展了《为家人选择合适的手机资费套餐》项目学习.以下是小露同学帮奶奶选择手机资费套餐的活动报告,请你将其补充完整.为家人选择合适的手机资费套餐活动报告
一、收集信息
收集并整理奶奶近六个月的话费账单,发现她使用流量和短信极少,故忽略流量和短信情况进行研究.根据她的月平均通话时间筛选出两款比较适合她的手机资费套餐.
甲套餐:月租费8元,送30分钟通话时间,超出的部分按每分钟0.25元计;
乙套餐:月租费29元,通话费按每分钟0.1元计.
二、建立模型
⑴.发现每月的手机资费y(元)与通话时间x(分)之间存在函数关系,y与x之间的关系式为:
, = ▲ (x≥0).
⑵.为了直观比较,在同一坐标系内画出两个函数的图象(如图).图中A点表示的实际意义是 ▲ .

⑶.解决问题
根据图象可知:如果从节省费用的角度考虑,
当通话时间 ▲ 时,选择甲套餐更合适;
当通话时间 ▲ 时,选择乙套餐更合适.
20. 【项目介绍】图①中的板凳又叫“四脚八叉凳”,是中国传统家具,图②是四脚八叉凳的几何示意图.四脚八叉凳的榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图③所示.板凳的结构设计体现了数学的对称美.
现在老师给同学们准备了凳面的木板和凳腿的木棒,请同学们根据要求准确找到榫眼的位置,安装板凳.
【驱动任务一】根据“四脚八叉凳”的几何示意图画出它的主视图,如图④.
【驱动任务二】如图⑤,若A、B、C在同一条直线上,且与地面垂直.小组同学选取的木棒作为凳脚进行制作,成品凳面与地面距离为 , 但是同学们发现此高度缺乏舒适感,所以决定重新调整打孔位置,经过计算发现,将榫眼外移多少时可将凳高调整为?
【驱动任务三】
根据做板凳的经验和对剩余材料的整理,同学们打算制作如图⑥所示的简易桌子,桌子的主视图如图⑦所示,正方形桌面的边长为 , 长的木棒恰好能截成和 , 则成品桌子的高度为多少?

 21. 思考探究:
21. 思考探究:【形成概念】城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.由此启发,我们可以按照街道的垂直和平行方向建立平面直角坐标系 , 对两点和 , 用以下方式定义两点间折线距离: .
(1)、【初步理解】①已知点 , 则 .
②函数的图象如图1所示,是图象上一点, , 则点的坐标是 .
(2)、【深入探究】某数学小组研究以下问题:是函数的图象上的一点,当的值最小,求点坐标.
小明同学从函数图象入手展开研究:
①绘制函数图象:
列表:
…
0
1
2
3
4
5
6
7
…
…
5
1
1
3
5
7
…
表格中:;
描点、连线:在平面直角坐标系(图2)中画出该函数图象;

②请写出一条函数的性质: .
(3)、观察图象: , 已知 , 求的最小值,并求出取得最小值时点坐标.22. 根据如表素材,探索完成任务.背景
深圳某学校在组织开展知识竞赛活动,去奶茶店购买A、B两种款式的奶茶作为奖品.
素材1
若买10杯A款奶茶,5杯B款奶茶,共需160元:若买15杯A型奶茶,10杯B型奶茶,共需270元.

素材2
为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完款式后可以自主选择加料一份或者不加料.
问题解决
任务1
问A款奶茶和B款奶茶的销售单价各是多少元?
任务2
在不加料的情况下,购买A、B两种款式的奶茶(两种都要),刚好花220元,请问有几种购买方案?
任务3
根据素材2,小华恰好用了380元购买A、B两款奶茶,其中A款不加料的杯数是总杯数的 . 则其中 B型加料的奶茶买了多少杯?