《一次函数》精选压轴题—广东省（北师版）八（上）数学期末复习

试卷更新日期：2025-01-01 类型：复习试卷

进入出卷网下载

一、单选题

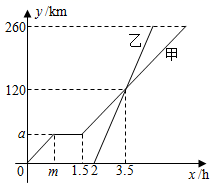
1. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距 $300$ 千米；
②乙车比甲车晚出发 $1$ 小时，却早到 $1$ 小时；
③乙车出发后 $1.5$ 小时追上甲车；
④当甲、乙两车相距 $50$ 千米时， $t = \frac{5}{4}$ 或 $\frac{15}{4}$
其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
2. 甲、乙两车从 $A$ 地出发，匀速驶往 $B$ 地．乙车出发 $1$ h后，甲车才沿相同的路线开始行驶．甲车先到达 $B$ 地并停留 $30$ 分钟后，又以原速按原路线返回，直至与乙车相遇．图中的折线段表示从开始到相遇止，两车之间的距离 $y (k m)$ 与甲车行驶的时间x（h）的函数关系的图象，则（）

A、甲车的速度是 $120 k m / h$ B、 $A$ ， $B$ 两地的距离是 $360 k m$ C、乙车出发4.5h时甲车到达 $B$ 地 D、甲车出发4.5h最终与乙车相遇

查看试题解析
3. 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶 $2 h$ ，并且甲车途中休息了 $0.5 h$ ，如图是甲、乙两车行驶的距离 $y (km)$ 与时间 $x (h)$ 的函数图象，有以下结论：
① $m = 1$ ；② $a = 40$ ；③甲车从A地到B地共用了7小时；④当两车相距 $50 km$ 时，乙车用时为 $\frac{1}{4} h$ .其中正确结论的个数是（）.

A、4 B、3 C、2 D、1

查看试题解析
4. 甲、乙两车从 $A$ 地出发，匀速驶往 $B$ 地.乙车出发1h后，甲车才沿相同的路线开始行驶.甲车先到达 $B$ 地并停留30分钟后，又以原速按原路线返回，直至与乙车相遇.图中的折线段表示从开始到相遇止，两车之间的距离 $y (k m)$ 与甲车行驶的时间 $x$ （h）的函数关系的图象，则（）

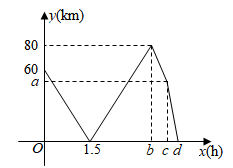A、甲车的速度是120km/h B、A，B两地的距离是360km C、乙车出发4.5h时甲车到达 $B$ 地 D、甲车出发4.5h最终与乙车相遇

查看试题解析
5. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息.已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙走完全程用了36分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有300米.其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在平面直角坐标系中，直线 $y = x + 2$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，点 $P$ 是线段 $A B$ 的中点，点 $C$ 是 $x$ 轴上的一个动点，连接 $B C$ ，以 $B C$ 为直角边，点 $B$ 为直角顶点作等腰直角 $△ B C D$ ，连接 $D P$ ．则 $D P$ 长度的最小值是（）

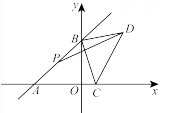A、1 B、2 C、 $2 \sqrt{2}$ D、3

查看试题解析
7. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A ， B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后1.5小时追上甲车；
④当甲、乙两车相距50千米时，t＝ $\frac{5}{4}$ 或 $\frac{15}{4}$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

8. A ， B两地相距20km ，甲从A地出发向B地前进，乙从B地出发向A地前进，两人沿同一直线同时出发，甲先以8km/h的速度前进1小时，然后减慢速度继续匀速前进，甲乙两人离A地的距离s（km）与时间t（h）的关系如图所示，则甲出发小时后与乙相遇．

查看试题解析
9. 如图；一只小蚂蚁在平面直角坐标系中按图中路线进行“爬楼梯”运动，第1次它从原点运动到点 $(1, 0)$ ，第2次运动到点 $(1, 1)$ ，第3次运动到点 $(2, 1) \dots \dots$ 按这样的运动规律，经过第2023次运动后，小蚂蚁的坐标是．

查看试题解析

三、解答题

10. 如图，直线L₁： $y = - x + 2$ 与 $x$ 轴， $y$ 轴分别交于A，B两点，点P（ $m$ ，3）为直线AB上一点，另一直线L₂： $y = k x + 4$ 经过点P．

(1)、求点A、B坐标；

(2)、求点P坐标和 $k$ 的值；

(3)、若点C是直线L₂与 $x$ 轴的交点，点Q是 $x$ 轴上一点，当△CPQ的面积等于3时，求出点Q的坐标

查看试题解析
11. 如图，正比例函数 $y = - 3 x$ 的图像与一次函数 $y = k x + b$ 的图像交于点 $P (m ， 3)$ ，一次函数图象经过点 $B (1 ， 1)$ ，与y轴的交点为D ，与x轴的交点为C ．

(1)、求一次函数表达式；

(2)、求D点的坐标；

(3)、求 $△ C O P$ 的面积．

查看试题解析
12. 如图，在平面直角坐标系中，过点C（0，6）的直线AC与直线OA相交于点A（4，2）．

(1)、求直线AC的表达式；

(2)、求△OAC的面积；

(3)、动点M在线段OA和射线AC上运动，是否存在点M，使△OMC的面积是△OAC的面积的 $\frac{1}{2}$ ？若存在，求出此时点M的坐标；若不存在，请说明理由。

查看试题解析
13. 如图，直线 $y = - x + 4$ 与坐标轴分别交于点 $A$ ， $B$ ，以 $O A$ 为边在 $y$ 轴的右侧作正方形 $A O B C$ ．

(1)、求点 $A$ ， $B$ 的坐标；

(2)、如图，点 $D$ 是 $x$ 轴上一动点，点 $E$ 在 $A D$ 的右侧， $∠ A D E = 90 °$ ， $A D = D E$ ．
$①$ 探究发现，点 $E$ 在一条定直线上，请直接写出该直线的解析式_▲_ ；
$②$ 若点 $D$ 是线段 $O B$ 的中点，另一动点 $H$ 在直线 $B E$ 上，且 $∠ H A C = ∠ B A D$ ，请求出点 $H$ 的坐标．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，正比例函数 $y = m x (m \neq 0)$ 的图象经过点 $A (2 ， 4)$ ，过点A的直线 $y = k x + b (0 < k < 2)$ 与x轴、y轴分别交于B ， C两点．

(1)、求正比例函数的表达式；

(2)、若 $△ A O B$ 的面积为 $△ B O C$ 的面积的 $\frac{4}{3}$ 倍，求直线 $y = k x + b$ 的表达式；

(3)、在（2）的条件下，在线段 $B C$ 上找一点D ，使 $O C$ 平分 $∠ A O D$ ，求点D的坐标．

查看试题解析
15. 如图1，在平面直角坐标系 $x O y$ 中，直线 $y = k x + b$ 分别与x轴，y轴交于点 $A (- 1 ， 0)$ ， $B (0 ， 2)$ ，过点 $C (2 ， 0)$ 作x轴的垂线，与直线 $A B$ 交于点D ．

(1)、求点D的坐标；

(2)、点 $E$ 是线段 $C D$ 上一动点，直线 $B E$ 与 $x$ 轴交于点 $F$ ．若 $△ B D F$ 的面积为8，求点F的坐标．

查看试题解析
16. 如图，在平面直角坐标系中，直线 $A B$ 与坐标轴相交于点 $A (0 ， 6)$ ， $B (8 ， 0)$ ，点 $C$ 是 $y$ 轴上一点．

(1)、求直线 $A B$ 的表达式．

(2)、如图1，连接 $B C$ ，将 $△ O B C$ 沿 $B C$ 翻折至 $△ E B C$ ，若点 $E$ 恰好落在直线 $A B$ 上，求点 $C$ 的坐标．

(3)、如图2，点 $F (2 ， 0)$ 在 $x$ 轴的正半轴上，连接 $C F$ ，将 $C F$ 绕点 $F$ 顺时针旋转 $45 °$ 至 $G F$ 的位置，连接 $B G$ ，请问 $B G$ 有最小值吗？如果有，请求出来；如果没有，请说明理由．

查看试题解析
17. 如图，直线 $y = - x + 4$ 与坐标轴分别交于点A，B，以OA为边在 $y$ 轴的右侧作正方形AOBC

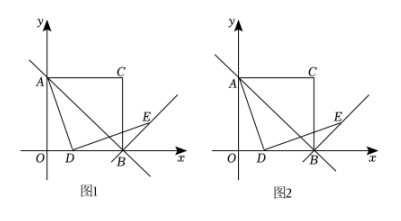(1)、求点A，B的坐标；

(2)、如图，点D是x轴上一动点，点E在AD的右侧， $∠ A D E = 9 0^{°} ， A D = D E$ .
①探究发现，点 $E$ 在一条定直线上，请直接写出该直线的解析式
②若点 $D$ 是线段OB的中点，另一动点 $H$ 在直线BE上，且 $∠ H A C = ∠ B A D$ ，请求出点 $H$ 的坐标.

查看试题解析

四、实践探究题

18. 定义：我们把一次函数 $y = k x + b (k \neq 0)$ 与正比例函数 $y = x$ 的交点称为一次函数 $y = k x + b (k \neq 0)$ 的“不动点”．例如求 $y = 2 x - 1$ 的“不动点”；联立方程 ${\begin{cases} y = 2 x - 1 \\ y = x \end{cases}$ ，解得 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，则 $y = 2 x - 1$ 的“不动点”为 $(1 ， 1)$ ．

(1)、由定义可知，求一次函数 $y = 3 x + 2$ 的“不动点”．

(2)、若一次函数 $y = m x + n$ 的“不动点”为 $(2 ， n - 1)$ ，求 $m 、 n$ 的值．

(3)、若直线 $y = k x - 3 (k \neq 0)$ 与x轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，且直线 $y = k x - 3$ 上没有“不动点”，若 $P$ 点为 $x$ 轴上一个动点，使得 $S_{△ A B P} = 3 S_{△ A B O}$ ，求满足条件的 $P$ 点坐标．

查看试题解析
19. 【定义】如图1，在同一平面内，点 $P ， Q$ 在线段 $M N$ 所在直线的两侧，若 $M P = N Q$ ，且 $∠ P M N = ∠ Q N M = 9 0^{∘}$ ，则称点 $P$ 与 $Q$ 是线段 $M N$ 的等垂对称点。

(1)、【理解】如图2，在正方形网格中，点 $A ， B ， C ， D ， E ， F$ 均在格点上，连接 $A B$ ，则下列各组点是线段 $A B$ 的等垂对称点的是；（填序号）
①点 $C$ 与点 $D$ ②点 $C$ 与点 $F$ ③点 $D$ 与点 $E$ ④点 $E$ 与点 $F$

(2)、如图3，在四边形 $A B C D$ 中， $E$ 是边 $B C$ 上一点，点 $B$ 与 $D$ 是线段 $A E$ 的等垂对称点，
①求证： $A D ∥ B C$ ；
②若 $D E$ 平分 $∠ A D C$ ，试探究 $∠ B C D$ 与 $∠ B$ 之间的数量关系，并说明理由。

(3)、【拓展】如图4，已知直线 $y = x + 4$ 与坐标轴交于点 $A ， B$ ，直线 $y = x - 2$ 与坐标轴交于点 $C ， D$ ，当点 $A ， B ， C ， D$ 中恰有两点是线段 $E F$ 的等垂对称点，且 $E F ∥ A B$ 时，请直接写出线段 $E F$ 的长。

查看试题解析