综合与实践—广东省（北师版）九（上）数学期末复习-在线组卷题库

1. 综合与实践

课题：小空间检测视力问题

具体情境：对某班学生视力进行检测的任务.

现有条件：一张测试距离为5米的视力表，一间长为3.8米，宽为3.6米的空书房.

(1)、如图，若将视力表挂在墙CDGH上，在墙ABEF上挂一面足够大的平面镜，根据平面镜成像原理可知：测试线应画在距离墙ABEF米处；

(2)、小明选择按比例制作视力表完成该任务.在制作过程中发现视力表上视力值V 和该行字母E的宽度a 之间的关系是已经学过的一类函数模型，字母 E 的宽度a 如上中图所示，视力表上部分视力值 V和字母E 的宽度a 的部分对应数据如右上表所示：

①请你根据表格数据判断(说明理由)并求出视力值 V与字母E 宽度a之间的函数关系式；

②小明在制作过程中发现某行字母E 的宽度a 的值17.5mm，请问该行对应的视力值是多少?

查看试题解析

2. 为弘扬中华优秀传统文化，坚定文化自信，展现对家乡、对祖国的热爱之情，某校组织了有关佛山非物质文化进产知识的竞答活动，并随机抽取了八年级若干名同学的成绩，形成了如下的调查报告.请根据报告中提供的信息，解答下列问题：

课题	佛山剪纸知识竞答成绩调查报告
问题展示	佛山剪纸，在制作上主要有哪些方式? 佛山剪纸的制作材料有哪些?……
数据的整理与描述	成绩/分	频数/人	频率	成绩/分	频数/ 人	频率
	第1组.90≤x≤100	12	0.2	第4组.60≤x<70	m	0.117
	第2组.70≤x<90	20	0.333	第5组.x<60	6	0.1
	第3组.70≤x<80	15	0.25

调查意义	了解佛山剪纸的知识，不仅能为同学们的美术色彩，工艺学习奠定基础，同时还能激发同学们对家乡的热爱.
调查结果

(1)、上述调查报告的数据收集方法是： (用“普查”或“抽样调查”填空)；

(2)、调查报告中的m 值是；在调查得到的数据中，中位数应该在第组；

(3)、将拍摄的“花”、 “竹”、“鸟”、 “兔”四张剪纸照片(除正面图案不同外，其余都相同)，背面朝上洗匀，甲、乙两同学随机各抽一张照片(不放回)做相关的知识介绍，请用树状图或列表的方式，求甲、乙两人恰好有一人抽到“花”的概率.

查看试题解析

3. 综合与实践

主题：X型晒衣架稳固性检测

步骤：如图甲是晒衣架的实物图，图乙是晒衣架侧面示意图，经测量得到立杆 $A B = C D = 136 c m$ ， $O A = O C = 51 c m ， O E = O F = 34 c m$ ，现将晒衣架完全稳固张开，横扣链 $E F$ 成一条线段，测得 $E F = 32 c m$ .

证明与计算：

(1)、连接

A C

，证明：

A C ∥ E F

；

(2)、利用夹子垂挂在晒衣架上的连衣裙（夹子高度忽略不计）总长度小于多少时，连衣裙才不会拖在地面上？

查看试题解析

4. 如图①，矩形

A B C D

的边

A B = 4 ， A D = 8

，将矩形

A B C D

绕点

A

逆时针旋转角

α (0^{∘} < α < 9 0^{∘})

得到矩形

A E F G

，

A D

与

E F

交于点

H

.

图① 图②

(1)、数学思考：填空：图①中

∠ A H F =

；（用含

α

的代数式表示）

(2)、深入探究：如图②，当点

H

在对角线

A C

的垂直平分线上时，连接

C H

，求证：

E H = D H

.

查看试题解析

5. 综合与实践

【问题背景】“夏至”过后，越来越多的市民喜欢去海边游玩，小明同学发现沙滩上有很多的遮阳伞为游客带来一丝清凉，如图1是沙滩上的圆形遮阳伞支架张开的状态，为了了解遮阳伞下方的遮阴面积，小明进行了如下操作调研．

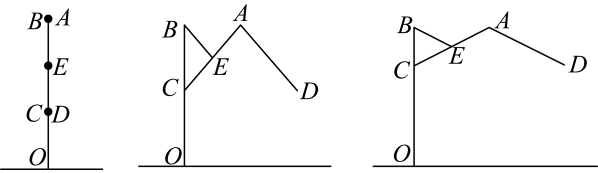
图1 图2 图3 图4

【测量与整理】通过操作发现，小明发现：如图2，当伞完全折叠时，伞顶 $A$ 与伞柄顶端点 $B$ 重合，两边主骨架的端点 $D$ 与 $C$ 重合；如图3，在撑开过程中，骨架 $A C$ 的中点 $E$ 到点 $B$ 的距离始终等于 $A C$ 的一半， $A C = A D = 150 c m$ ；如图4，当伞完全张开时， $3 A C = 5 B C$ ．

【计算与分析】

(1)、当伞完全张开后，求

D C

的长度；

(2)、当太阳光垂直照到遮阳伞上时，求伞完全张开时，遮挡住的阴影部分的面积．

查看试题解析

6. 生物学上通常用“标记重捕法”来估算特定区域内某种群的数量．如在固定区域内用捕虫网捕捉了40只田鼠，将它们标记后放回直到充分混合后，用同一个捕虫网捕捉了80只田鼠，其中有16只是被标记的，于是估算该区域田鼠的数量为：

$N = 40 \div \frac{16}{80} = 200$ （只）．

某研究小组考察了一湖泊中的某鱼种群的年龄组成，结果如下表，请回答问题：

年龄	A	B	C	D	……
个体数量	92	187	x	y	……

注：表中“ $A$ ”表示鱼的年龄 $0 - 1$ 年， $B$ 表示年龄 $2 - 3$ 年， $C$ 表示年龄 $4 - 5$ 年， $D$ 表示年龄为 $6 - 7$ 年．

(1)、年龄为

A

，

B

，

C

的个体数量的平均数为125，年龄在

A

，

B

，

C

，

D

的个体数量的中位数是95，则

x =

，

y =

（其中

92 < y < 96

）．

(2)、若将年龄为

D

的鱼全部标记后并放回湖泊，充分混合后，捕捉120条鱼，其中被标记鱼有12条，那么该湖泊里一共约有多少条鱼？

(3)、现捕获A，B，C，D年龄段的鱼各一条，从中任抓两条，请用列表或画树状图求抓到的是

A

和

C

年龄的鱼的概率．

查看试题解析

7.

【综合与探究】问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知 $A D$ 是 $△ A B C$ 的角平分线，可证 $\frac{A B}{A C} = \frac{B D}{C D}$ ．小慧的证明思路是：如图2，过点 $C$ 作 $C E ∥ A B$ ，交 $A D$ 的延长线于点 $E$ ，构造相似三角形来证明 $\frac{A B}{A C} = \frac{B D}{C D}$ ．

(1)、尝试证明：请参照小慧提供的思路，利用图2证明：

\frac{A B}{A C} = \frac{B D}{C D}

；

(2)、应用拓展：如图3，在

R t △ A B C

中，

∠ B A C = 90 ° ， D

是边

B C

上一点．连接

A D

，将

△ A C D

沿

A D

所在直线折叠，点

C

恰好落在边

A B

上的

E

点处．

①若 $A C = 1 ， A B = 2$ ，求 $D E$ 的长；

②若 $B C = m ， ∠ A E D = α$ ，求 $D E$ 的长（用含 $m ， α$ 的式子表示）．

查看试题解析

8. 在一堂数学课上，张老师要求同学们在一张长 12 cm 、宽 5 cm 的矩形纸片内折出一个菱形，甲同学很快想了一个办法，他将较短的一条边与较长一边重合，展开后得到四边形

A B E F

(见图 1)；乙同学按照取两组对边中点的方法折出四边形

E F G H

(见图 2)；丙同学也不甘示弱，他沿矩形的对角线

A C

折出

∠ C A E = ∠ D A C, ∠ A C F = ∠ A C B

，得到四边形

A E C F

(见图 3). 请解答下列问题：

(1)、关于甲、乙两位同学的做法描述正确的是____

A、甲、乙都得到菱形 B、甲、乙都没得到菱形 C、只有甲得到菱形 D、只有乙得到菱形

(2)、证明丙同学得到的四边形

A E C F

是菱形.

查看试题解析

9. 【综合与实践】：阅读材料，并解决以下问题．

【学习研究】：北师大版教材九年级上册第39页介绍了我国数学家赵爽在其所著的《勾股圆方图注》中关于一元二次方程的几何解法：以 $x^{2} + 2 x - 35 = 0$ 为例，构造方法如下：

首先将方程 $x^{2} + 2 x - 35 = 0$ 变形为 $x (x + 2) = 35$ ，然后画四个长为 $x + 2$ ，宽为 $x$ 的矩形，按如图（1）所示的方式拼成一个“空心”大正方形，则图中大正方形的面积可表示为 $(x + x + 2)^{2}$ ，还可表示为四个矩形与一个边长为2的小正方形面积之和，即 $4 x (x + 2) + 2^{2} = 4 \times 35 + 4$ ，因此，可得新方程： $(x + x + 2)^{2} = 144$ ， $∵ x$ 表示边长， $∴ 2 x + 2 = 12$ ，即 $x = 5$ ，遗憾的是，这样的做法只能得到方程的其中一个正根．

【类比迁移】：小明根据赵爽的办法解方程 $x^{2} + 3 x - 4 = 0$ ，请你帮忙画出相应的图形，将其解答过程补充完整：

第一步：将原方程变形为 $x^{2} + 3 x - 4 = 0$ ，即 $x$ （ ▲ ）=4；

第二步：利用四个面积可用 $x$ 表示为 ▲ 的全等矩形构造“空心”大正方形（请在画图区画出示意图，标明各边长），并写出完整的解答过程；

第三步：

【拓展应用】：一般地对于形如： $x^{2} + a x = b$ 一元二次方程可以构造图2来解，已知图2是由4个面积为3的相同矩形构成，中间围成的正方形面积为4．那么此方程的系数 $a =$ ▲ ， $b =$ ▲ ，求得方程的一个正根为 ▲ ．

查看试题解析

10. 某数学学习小组学习完四边形后进行了如下探究，已知四边形 EFGH 为矩形，请你帮助他们解决下列问题：

(1)、【初步尝试】：他们将矩形 EFGH 的顶点 E、G 分别在如图（1）所示的▱ABCD 的边 AD、BC 上，顶点 F、H 恰好落在▱ABCD 的对角线 BD 上，求证：BF＝DH

(2)、【深入深究】：如图 2，若口

A B C D

为菱形，

∠ A B C = 6 0^{°}

，若

A E = E D

，求

\frac{s_{菱 形 A B C D}}{s_{矩 形 E F G H}}

的值；

(3)、【拓展延伸】：如图（3），若▱ABCD 为矩形，AD=m；AB=n 且 AE=ED，请直接写出此时

\frac{s_{菱 形 A B C D}}{s_{矩 形 E F G H}}

的值是（用含有m，n的代数式表示）

查看试题解析

11. 【综合与实践】：北师大版九年级上册数学教材第 122 页第 21 题：“怎样把一块三角形的木板加工成一个面积最大的正方形桌面？”某小组同学对此展开了思考。

(1)、【特例感知】：若木板的形状是如图（甲）所示的直角三角形，

S_{△ B B C} = 1.5 m^{2} ， A B = 1.5 m

，根据 “相似三角形对应的高的比等于相似比”可以求得此时正方形 DEFG 的边长.

(2)、【问题解决】：若木板是面积仍然为 1.5m 2 的锐角三角形 ABC，按照如图（乙）所示的方式加工，记所得的正方形 DEFG 的面积为 S，如何求 S 的最大值呢？某学习小组做了如下思考：

设 $D E = x ， A C = a ， A C$ 边上的高 $B H = h$ ，则 $S_{△ A B C} = \frac{1}{2} a h ， ∴ h = \frac{3}{a}$ ，由 $△ B D E - △ B A C$ 得： $\frac{B M}{B H} = \frac{D E}{A C}$ ，从而可以求得 $x = \frac{2 S}{a + h}$ ，若要内接正方形面积 $S$ 最大，即就是求 $x$ 的最大值，因为 $S = 1.5$ 为定值，因此只需要分母最小即可。

小组同学借鉴研究函数的经验，令 $y = a + h = a + \frac{2 s}{a} = a + \frac{3}{a} (a > 0)$ . 探索函数 $y = a + \frac{3}{a}$ 的图象和性质：

①下表列出了 y 与 a 的几组对应值，其中m=____.

②在如图（丙）所示的平面直角坐标系中画出该函数的大致图象； ③结合表格观察函数 $y = a + \frac{3}{a}$ 图象，以下说法正确的是____。

A、当 a＞1时， y 随 a 的增大而增大. B、该函数的图象可能与坐标轴相交. C、该函数图象关于直线y=a对称. D、当该函数取最小值时，所对应的自变量 a 的取值范围在1～ 2。

查看试题解析

12. 综合应用

【问题情境】

在正方形纸片ABCD中，AB=6，点P是边AD 上的一个动点，过点P作PQ∥AB 交 BC于点Q，将正方形纸片ABCD折叠，使点C的对应点C落在线段PQ上，点B的对应点为B'，折痕所在的直线交边AB于点E、交边 CD于点F，EF与PQ交于点N.

【猜想证明】

(1)、如图，连接CN，则四边形CNC'F 是_▲_形，请说明理由.

(2)、如图，当E与B重合时，

①若AP=3，求 CF的长.

② 记AP 的长度为y，线段CF长度为x，求y与x之间的关系式，并直接写出当F是CD的三等分点时， AP 的长度.

查看试题解析

13. 综合运用

在矩形 $O A B C$ 中，以点 $O$ 为坐标原点，分别以 $O C ， O A$ 所在直线为 $x$ 轴、 $y$ 轴，建立平面直角坐标系，点 $E$ 是射线 $O C$ 上一动点，连接 $A E$ ，过点 $O$ 作 $O F ⊥ A E$ 于点 $D$ ，交直线 $B C$ 于点 $F$ .

图① 图② 图③

(1)、如图①，当矩形

O A B C

是正方形时，若点

E

在线段

O C

上，线段

A E

与

O F

的数量关系是（填“相等”或“不相等”）；

(2)、如图②，当点

E

在线段

O C

上，且

O E = 2 E C

，以点

F

为直角顶点在矩形

O A B C

的外部作直角三角形

C F H

，且

F H = O E

，连接

E H

，交

B C

于点

G

，求

\frac{S_{△ F G H}}{S_{四 边 形 O E G F}}

的值；

(3)、如图③，若点

A (0 ， 3)

，点

C (1 ， 0)

，点

E

在线段

O C

的延长线上，点

F

在线段

C B

的延长线上，

F H ⊥ F C ， F B ： B C = 1 ： 3

，连接

O H

，取

O H

的中点

M

，连接

D M

，设

F H = n

，

D M^{2} = m

，求

m

关于

n

的函数关系式.

查看试题解析

14. 问题提出：如图1，E是菱形

A B C D

边

B C

上一点，

△ A E F

是等腰三角形，

A E = E F

，

∠ A E F = ∠ A B C = β (β \geq 90 °)

，

A F

交

C D

于点G ，探究

∠ G C F

与β的数量关系．

问题探究：

(1)、先将问题特殊化，如图2，当

β = 90 °

时，求

∠ G C F

的度数；

(2)、再探究一般情形，如图1，求

∠ G C F

与β的数量关系；

问题拓展：

将图1特殊化，如图3，当 $A B = 3$ ， $β = 120 °$ ，且 $\frac{D G}{C G} = \frac{1}{2}$ 时，求 $C F$ 的值．

查看试题解析

15. 综合与实践

(1)、探究发现：如图1，在

4 \times 3

的网格图中，在线段

A B

上求一点

P

，使得

B P = \frac{1}{2} A P

；小明同学发现，先在点

B

的左侧取点

C

，使

B C

为1个单位长度，在点

A

的右侧取点

D

，使

A D

为2个单位长度，然后连接

C D

交

A B

于点

P

（如图1），就可以得到点

P

了．请你验证小明的做法，并求出

t a n ∠ A P C

的值．

(2)、请你在图2中求作一点

P

，使得

B P = \frac{2}{3} A P

．

查看试题解析

16. 某数学学习小组学习完四边形后进行了如下探究，已知四边形

E F G H

为矩形，请你帮助他们解决下列问题：

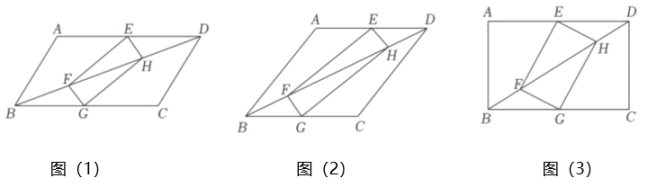(1)、【初步尝试】：他们将矩形

E F G H

的顶点E、G分别在如图（1）所示的

▱ A B C D

的边

A D

、

B C

上，顶点F、H恰好落在

▱ A B C D

的对角线

B D

上，求证：

B F = D H

：

(2)、【深入探究】：如图2，若

▱ A B C D

为菱形，

∠ A B C = 60 °

，若

A E = E D

，求

\frac{S_{菱 形 A B C D}}{S_{矩 形 E F G H}}

的值；

(3)、【拓展延伸】：如图（3），若

▱ A B C D

为矩形，

A D = m

；

A B = n

且

A E = E D

，请直接写出此时

\frac{S_{矩 形 A B C D}}{S_{矩 形 E F G H}}

的值是（用含有m ， n的代数式表示）.

查看试题解析

17. 【综合与实践】：北师大版九年级上册数学教材第122页第21题：“怎样把一块三角形的木板加工成一个面积最大的正方形桌面？”某小组同学对此展开了思考.

(1)、【特例感知】：若木板的形状是如图（甲）所示的直角三角形，

S_{△ A B C} = 1.5 m^{2}

，

A B = 1.5 m

，根据“相似三角形对应的高的比等于相似比”可以求得此时正方形

D E F G

的边长是.

(2)、【问题解决】：若木板是面积仍然为

1.5 m^{2}

的锐角三角形

A B C

，按照如图（乙）所示的方式加工，记所得的正方形

D E F G

的面积为S ，如何求S的最大值呢？某学习小组做了如下思考：

设 $D E = x$ ， $A C = a$ 、 $A C$ 边上的高 $B H = h$ ，则 $S_{△ A B C} = \frac{1}{2} a h$ ， ∴ $h = \frac{3}{a}$ ，由 $△ B D E$ - $△ B A C$ 得： $\frac{B M}{B H} = \frac{D E}{A C}$ ，从而可以求得 $x = \frac{2 S}{a + h}$ ，若要内接正方形面积S最大，即就是求x的最大值。因为 $S = 1.5$ 为定值，因此只需要分母最小即可.

小组同学借鉴研究函数的经验，令 $y = a + h = a + \frac{2 s}{a} = a + \frac{3}{a} (a > 0)$ .探索函数 $y = a + \frac{3}{a}$ 的图象和性质：

①下表列出了y与a的几组对应值，其中 ▲ ；

a	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	$\frac{3}{2}$	2	3	4	…
y	…	$12 \frac{1}{4}$	$9 \frac{1}{3}$	m	4	$3 \frac{1}{2}$	$3 \frac{1}{2}$	4	$4 \frac{3}{4}$	…

②在如图（丙）所示的平面直角坐标系中画出该函数的大致图象；

③结合表格观察函数 $y = a + \frac{3}{a}$ 图象，以下说法正确的是 ▲ .

A.当 $a > 1$ 时，y随a的增大而增大.

B.该函数的图象可能与坐标轴相交.

C.该函数图象关于直线 $y = a$ 对称.

D.当该函数取最小值时，所对应的自变量a的取值范围在 $1 ~ 2$ 之间.

查看试题解析

18.

(1)、【模型发现】如图1，△ABC∽△ADE，求证：△ABD∽△ACE．

(2)、【深入探究】如图2，等边△ABC中，AB＝3，D是AC上的动点，连接BD，将BD绕着点D逆时针旋转60°得到DE，连接CE，当点D从A运动到C时，求点E的运动路径长．

(3)、【应用拓展】如图3，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于D，E是AD上的一点，连接BE，将BE绕着点E逆时针旋转90°，得到EF，EF交BC于点G，连接CF，若EG=

\frac{1}{2}

FG，则

\frac{A B}{C F}

的值为．

查看试题解析

19. 探索一个问题： "任意给定一个矩形

A

，是否存在另一个矩形

B

，它的周长和面积分别是已知矩形周长和面积的一半? "

(1)、完成下列空格：

当已知矩形 $A$ 的边长分别为 6 和 1 时，小明是这样研究的：设所求矩形 B 的一边是 $x$ ，则另一边为 $(\frac{7}{2} - x)$ ，由题意得方程： $x (\frac{7}{2} - x) = 3$ ，化简得：

$2 x^{2} - 7 x + 6 = 0$

$b^{2} - 4 a c = 49 - 48 > 0$

解得： $x_{1} =$ ， $x_{2} =$ .

$∴$ 满足要求的矩形 $B$ 存在.

小红的做法是：设所求矩形的两边分别是 $x$ 和 $y$ ，由题意得方程组： $\{\begin{array}{l} x + y = \frac{7}{2} \\ x y = 3 \end{array}$ 消去 $y$ 化简后也得到： $2 x^{2} - 7 x + 6 = 0$ ， (以下同小明的做法)

(2)、如果已知矩形

A

的边长分别为 2 和 1 时，请你仿照小明或小红的方法研究是否存在满足要求的矩形

B

.

(3)、在小红的做法中，我们可以把方程组整理为：

\{\begin{array}{l} y = \frac{7}{2} - x \\ y = \frac{3}{x} \end{array}

，此时两个方程都可以看成是函数表达式，从而我们可以利用函数图象解决一些问题. 仿照这种方法，如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中

x

和

y

分别表示矩形

B

的两边长，直线经过点

(0,4.5) 、 (4.5,0)

，双曲线经过点

P (4,1)

，请你结合刚才的研究，回答下列问题：（完成下列空格）

①这个图象所研究的矩形 $A$ 的面积为；周长为.

②满足条件的矩形 $B$ 的两边长为和.

查看试题解析

20. 【定义】在平面内，把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值，称为这两个图形之间的距离，即A，B分别是图形

M

和图形

N

上任意一点，当AB的长最小时，称这个最小值为图形

M

与图形

N

之间的距离.

例如，如图1， $A B ⊥ l_{1}$ ，线段AB的长度称为点， $A$ 与直线 $l_{1}$ 之间的距离，当 $l_{2} / l_{1}$ 时，线段AB的长度也是 $l_{1}$ 与 $l_{2}$ 之间的距离.

【应用】

(1)、如图2，在等腰Rt

△ B A C

中，

∠ A = 9 0^{°} ， A B = A C

，点

D

为AB边上一点，过点

D

作

D E ‖ B C

交AC于点

E

.若

A B = 6 ， A D = 4

，则DE与BC之间的距离是

(2)、如图3，已知直线

l_{3} ： y = - x + 4

与双曲线

C ： y = \frac{k}{x} (x > 0)

交于

A (1 ， m)

与

B

两点，点

A

与点，

B

之间的距离是，点

O

与双曲线

C_{1}

之间的距离是；

(3)、【拓展】按规定，住宅小区的外延到高速路的距离不超过80m时，需要在高速路旁修建与高速路相同走向的隔音屏障（如图4）.有一条“东南-西北”走向的笔直高速路，路旁某住宅小区建筑外延呈双曲线的形状，它们之间的距离小于80m.现以高速路上某一合适位置为坐标原点，建立如图5所示的直角坐标系，此时高速路所在直线l4的函数表达式为

y = - x

，小区外延所在双曲线

C_{2}

的函数表达式为

y = \frac{2400}{x} (x

> 0)

，那么需要在高速路旁修建隔音屏障的长度是多少？

查看试题解析

21. 矩形

A B C D

中，

\frac{A B}{B C} = \frac{k}{2} (k > 1)

，点E是边BC的中点，连接AE，过点E作AE的垂线EF，与矩形的外角平分线CF交于点F．

(1)、【特例证明】如图，当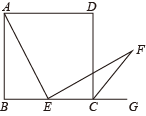

k = 2

时，求证：

A E = E F

；

(2)、【类比探究】如图，当

k \neq 2

时，求

\frac{A E}{E F}

的值（用含k的式子表示）；

(3)、【拓展运用】如图，当

k = 3

时，P为边CD上一点，连接AP，PF，

∠ P A E = 45 °

，

P F = 2 \sqrt{5}

，则BC的长为．

查看试题解析

综合与实践—广东省（北师版）九（上）数学期末复习

一、综合与实践