精选压轴题—广东省(北师版)九(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、选择题
-
1. 如图,菱形ABCD的面积为24,对角线AG与BD交于点O,E是BC边的中点, 于点F, 于点G,则四边形EFOG的面积为( )
 A、3 B、5 C、6 D、82. 如图,在正方形中,为的中点,为上一点(不与 , 重合),将沿所在的直线折叠,得到 , 连接 . 当时,的值是( )
A、3 B、5 C、6 D、82. 如图,在正方形中,为的中点,为上一点(不与 , 重合),将沿所在的直线折叠,得到 , 连接 . 当时,的值是( )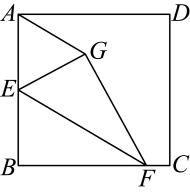 A、1 B、 C、 D、3. 如图,矩形ABCD中 ,AD>AB,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E ,F. 若AB=4,BC=8,则四边形AFCE面积是( )
A、1 B、 C、 D、3. 如图,矩形ABCD中 ,AD>AB,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E ,F. 若AB=4,BC=8,则四边形AFCE面积是( ) A、20 B、16 C、12 D、244. 如图,在正方形ABCD外取一点 , 连接AE、BE、DE.过点作AE的垂线交DE于点.若.下列结论:①;②点到直线AE的距离是;③;④.其中正确的结论是( )
A、20 B、16 C、12 D、244. 如图,在正方形ABCD外取一点 , 连接AE、BE、DE.过点作AE的垂线交DE于点.若.下列结论:①;②点到直线AE的距离是;③;④.其中正确的结论是( ) A、①② B、①④ C、①③④ D、①②③
A、①② B、①④ C、①③④ D、①②③二、填空题
-
5. 在平面直角坐标系中,已知 , 在轴上有一点 , 它与两点形成的三角形与相似(全等除外),则点的坐标是.6. 如图,P是的斜边(不与点A、C重合)上一动点,分别作于点M,于点N,O是的中点,若 , , 当点P在上运动时,的最小值是 .
 7. 如图,矩形对角线相交于点 , 沿着对角线折叠,使得点落在点处,其中点的坐标为长度为 , 则的纵坐标为 .
7. 如图,矩形对角线相交于点 , 沿着对角线折叠,使得点落在点处,其中点的坐标为长度为 , 则的纵坐标为 .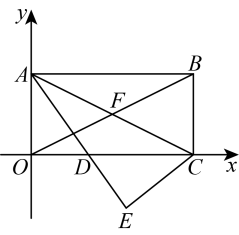 8. 如图,为直角三角形, , , , D是边上的中点,将绕着点A逆时针旋转,使点C落在线段上的点E处,点B的对应点为F , 边与边交于点G , 则的长是.
8. 如图,为直角三角形, , , , D是边上的中点,将绕着点A逆时针旋转,使点C落在线段上的点E处,点B的对应点为F , 边与边交于点G , 则的长是. 9. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
9. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .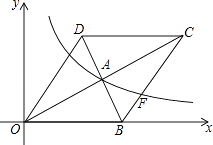
三、解答题
-
10. 如图,在矩形ABCD中,AB=4cm,BC=11cm,点P从点D出发向终点A运动;同时点Q从点B出发向终点C运动.当P、Q两点其中有一点到达终点时,另一点随之停止,点P、Q的速度分别为1cm/s,2cm/s,连接PQ、AQ、CP.设点P、Q运动的时间为t(s).
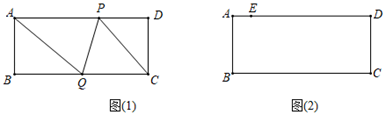 (1)、如图(1),当t为何值时,四边形ABQP是矩形?(2)、如图(2),若点E为边AD上一点,当AE=3cm时,四边形EQCP可能为菱形吗?若能,请求出t的值;若不能,请说明理由.11.
(1)、如图(1),当t为何值时,四边形ABQP是矩形?(2)、如图(2),若点E为边AD上一点,当AE=3cm时,四边形EQCP可能为菱形吗?若能,请求出t的值;若不能,请说明理由.11.【综合与探究】问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知是的角平分线,可证 . 小慧的证明思路是:如图2,过点作 , 交的延长线于点 , 构造相似三角形来证明 .
 (1)、尝试证明:请参照小慧提供的思路,利用图2证明:;(2)、应用拓展:如图3,在中,是边上一点.连接 , 将沿所在直线折叠,点恰好落在边上的点处.
(1)、尝试证明:请参照小慧提供的思路,利用图2证明:;(2)、应用拓展:如图3,在中,是边上一点.连接 , 将沿所在直线折叠,点恰好落在边上的点处.①若 , 求的长;
②若 , 求的长(用含的式子表示).
12. 过四边形的顶点A作射线 , P为射线上一点,连接 . 将绕点A顺时针方向旋转至 , 记旋转角 , 连接 . (1)、如图1,数学兴趣小组探究发现,如果四边形是正方形,且 . 无论点P在何处,总有 , 请证明这个结论.(2)、如图2,如果四边形是菱形, , , 连接 . 当 , 时,求的长;(3)、如图3,如果四边形是矩形, , , 平分 , . 在射线上截取 , 使得 . 当是直角三角形时,请直接写出的长.13. 已知点在反比例函数的图象上,以为边长作正方形 , 使正方形顶点在轴上方,与轴的夹角为 .
(1)、如图1,数学兴趣小组探究发现,如果四边形是正方形,且 . 无论点P在何处,总有 , 请证明这个结论.(2)、如图2,如果四边形是菱形, , , 连接 . 当 , 时,求的长;(3)、如图3,如果四边形是矩形, , , 平分 , . 在射线上截取 , 使得 . 当是直角三角形时,请直接写出的长.13. 已知点在反比例函数的图象上,以为边长作正方形 , 使正方形顶点在轴上方,与轴的夹角为 .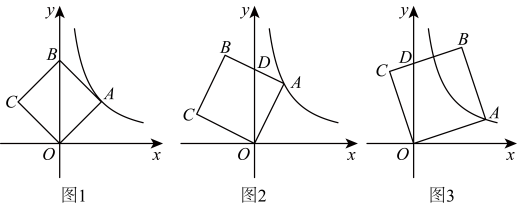 (1)、如图1,当点在轴上时,求点坐标;(2)、①如图2,当时,与轴相交于点 , 若 , 求点的坐标;
(1)、如图1,当点在轴上时,求点坐标;(2)、①如图2,当时,与轴相交于点 , 若 , 求点的坐标;②如图3,当时,与轴相交于点 , 若 , 求点的坐标.
14. 某数学学习小组学习完四边形后进行了如下探究,已知四边形为矩形,请你帮助他们解决下列问题: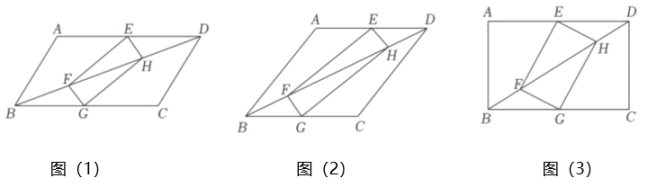 (1)、【初步尝试】:他们将矩形的顶点E、G分别在如图(1)所示的的边、上,顶点F、H恰好落在的对角线上,求证::(2)、【深入探究】:如图2,若为菱形, , 若 , 求的值;(3)、【拓展延伸】:如图(3),若为矩形,;且 , 请直接写出此时的值是(用含有m , n的代数式表示).15. 综合应用
(1)、【初步尝试】:他们将矩形的顶点E、G分别在如图(1)所示的的边、上,顶点F、H恰好落在的对角线上,求证::(2)、【深入探究】:如图2,若为菱形, , 若 , 求的值;(3)、【拓展延伸】:如图(3),若为矩形,;且 , 请直接写出此时的值是(用含有m , n的代数式表示).15. 综合应用【问题情境】
在正方形纸片ABCD中 ,AB=6,点P是边AD 上的一个动点,过点P作PQ∥AB 交 BC于点Q,将正方形纸片ABCD折叠,使点C的对应点C落在线段PQ上,点B的对应点为B',折痕所在的直线交边AB于点E、交边 CD于点F,EF与PQ交于点N.
【猜想证明】
(1)、如图,连接CN,则四边形CNC'F 是_▲_形,请说明理由.(2)、如图,当E与B重合时,①若AP=3,求 CF的长.
② 记AP 的长度为y,线段CF长度为x,求y与x之间的关系式,并直接写出当F是CD的三等分点时, AP 的长度.
16. 综合运用在矩形中,以点为坐标原点,分别以所在直线为轴、轴,建立平面直角坐标系,点是射线上一动点,连接 , 过点作于点 , 交直线于点.

图① 图② 图③
(1)、如图①,当矩形是正方形时,若点在线段上,线段与的数量关系是(填“相等”或“不相等”);(2)、如图②,当点在线段上,且 , 以点为直角顶点在矩形的外部作直角三角形 , 且 , 连接 , 交于点 , 求的值;(3)、如图③,若点 , 点 , 点在线段的延长线上,点在线段的延长线上, , 连接 , 取的中点 , 连接 , 设 , , 求关于的函数关系式.17. 问题提出:如图1,E是菱形边上一点,是等腰三角形, , , 交于点G , 探究与β的数量关系.
问题探究:
(1)、先将问题特殊化,如图2,当时,求的度数;(2)、再探究一般情形,如图1,求与β的数量关系;问题拓展:
将图1特殊化,如图3,当 , , 且时,求的值.
18. 某校数学活动小组在一次活动中,对一个数学问题作如下探究. (1)、【问题发现】
(1)、【问题发现】如图①,在等边中,点是边BC上一点,且 , 连接AP,以AP为边作等边 , 连接CQ.则CQ的长为;
(2)、【问题提出】如图②,在等腰中, , 点是边BC上任意一点,以AP为腰作等腰 , 使 , 连接CQ.试说明与相等;
(3)、【问题解决】如图③,在正方形ADBC中,点是边BC上一点,以AP为边作正方形APEF,点是正方形APEF的对称中心,连接CQ.若正方形APEF的边长为12, , 求正方形ADBC的边长.