阅读理解题—浙江省七(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、阅读理解题
-
1. 阅读下面的解题过程,并用解题过程中的解题方法解决问题.
示例:计算: .
解:原式
.
以上解题方法叫做拆项法.
请你利用拆项法计算下面式子的值.
2. 先阅读材料,再解决问题.阅读材料:有一间活动室地面由A和B两种正方形地砖铺成,活动室地面也是正方形,已知:
A地砖使用了36块,每块面积为xcm2 , 每平米单价为50元;
B地砖使用了217块,每块面积为ycm2 , 每平米单价为16元;
(1)、用x,y表示铺设活动室地面的费用。(2)、试说出代数式 所表示的的实际含义。3. 【数学中的阅读理解】对于实数 , 我们规定:用符号表示不大于的最大整数,称的根整数,例如: .(1)、【阅读理解】仿照以上方法计算: , ;(2)、【解决问题】若 , 写出满足题意的的整数值;(3)、【扩展探究】①如果我们对连续求根整数,直到结果是1为止.例如:对10连续求根整数2次 , 这时候结果为1.则对有理数137连续求根整数,几次之后结果是1;②试求出只需进行3次连续求根整数运算后结果是1的所有正整数中最大的数。
4. 阅读材料:我们定义:如果两个实数的和等于这两个实数的积,那么这两个实数就叫做“和积等数对”,即:如果 , 那么a与b就叫做“和积等数对”,记为.
例如: , , ,
则称数对 , , 是“和积等数对”.
根据上述材料,解决下列问题:
(1)、下列数对中,“和积等数对”是 填序号;①; ②; ③.
(2)、如果是“和积等数对”,请求出x的值;(3)、如果是“和积等数对”,那么m=(用含的代数式表示).5. 原题呈现:代数式:的值为9.则代数式的值为.【阅读理解】小明在做作业时采用的方法如下:(∵表示“因为”,∴表示“所以”)
∵ , ∴ .
原式 .
∴代数式的值为9.
(1)、【方法运用】若 , 则 .(2)、若代数式的值为15,求代数式的值.(3)、【拓展应用】若 , , 测代数式的值为 .6. 阅读下面的材料:小明在复习过程中发现可以用“两数的差”来表示“数轴上两点之间的距离”.如图1,若线段在数轴上,A,B点表示的数分别为a, , 则线段的长(点A到点B的距离)可表示为(较大数较小数).
请用上面材料中的知识解答下面的问题:
 (1)、如图2,点A表示数x,点B表示数 , 点C表示数 , 且 , 求点A,点C所表示的数;(2)、在(1)的条件下,若点M从点A出发,以每秒4个单位长度的速度向右移动,同时点N从点C出发,以每秒6个单位长度的速度向左移动,当点N到达点B后立即以原来的速度向右移动.设移动时间为t秒,当时,求t的值.7. 【阅读理解】射线OC是内部的一条射线,若 , 则我们称射线OC是射线OA的“友好线”.例如,如图1, , 则 , 称射线OC是射线OA的友好线;同时,由于 , 称射线OD是射线OB的友好线.
(1)、如图2,点A表示数x,点B表示数 , 点C表示数 , 且 , 求点A,点C所表示的数;(2)、在(1)的条件下,若点M从点A出发,以每秒4个单位长度的速度向右移动,同时点N从点C出发,以每秒6个单位长度的速度向左移动,当点N到达点B后立即以原来的速度向右移动.设移动时间为t秒,当时,求t的值.7. 【阅读理解】射线OC是内部的一条射线,若 , 则我们称射线OC是射线OA的“友好线”.例如,如图1, , 则 , 称射线OC是射线OA的友好线;同时,由于 , 称射线OD是射线OB的友好线.【知识运用】
 (1)、如图2, , 射线OM是射线OA的友好线,则为多少度;(2)、如图3, , 射线OC与射线OA重合,并绕点以每秒的速度逆时针旋转,射线OD与射线OB重合,并绕点以每秒的速度顺时针旋转,当射线OD与射线OA重合时,运动停止;
(1)、如图2, , 射线OM是射线OA的友好线,则为多少度;(2)、如图3, , 射线OC与射线OA重合,并绕点以每秒的速度逆时针旋转,射线OD与射线OB重合,并绕点以每秒的速度顺时针旋转,当射线OD与射线OA重合时,运动停止;①是否存在某个时刻t(秒),使得∠COD的度数是 , 若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线OC、OD、OA中恰好有一条射线是另一条射线的友好线.
8. 阅读材料:定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的 , 则称该点是其他两个点的“倍分点”.例如,数轴上点A,B,C所表示的数分别为–1,0,2,且满足 , 则点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.
 (1)、基础巩固:在A,B,C三点中,点是点M,N的“倍分点”.(2)、尝试应用:若数轴上点M是点A,D的“倍分点”,则点D在数轴上对应的数有_____________个.(3)、灵活运用:若数轴上点N是点P,M的“倍分点”,且点Р在点N的右侧,求此时点Р在数轴上表示的数.9. 【阅读材料】
(1)、基础巩固:在A,B,C三点中,点是点M,N的“倍分点”.(2)、尝试应用:若数轴上点M是点A,D的“倍分点”,则点D在数轴上对应的数有_____________个.(3)、灵活运用:若数轴上点N是点P,M的“倍分点”,且点Р在点N的右侧,求此时点Р在数轴上表示的数.9. 【阅读材料】我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离,若点M表示的数 , 点N表示的数是 , 点M在点N的右边(即),则点M,N之间的距离为 , 即 . 例如:若点C表示的数是 , 点D表示的数是 , 则线段 .
【理解应用】
(1)已知在数轴上,点E表示的数是 , 点F表示的数是 , 求线段的长;
【拓展应用】
如图,数轴上有三个点,点A表示的数是 , 点B表示的数是3,点P表示的数是x.
(2)当A,B,P三个点中,其中一个点是另外两个点所连线段的中点时,则__________;
(3)数轴上是否存在一点Q,使点Q到点A,点B的距离和为21?若存在,求出点Q表示的数;若不存在,请说明理由.
 10. 我们知道分数写为小数形式即 , 反过来,无限循环小数写为分数形式即一般地,任何一个无限循环小数都可以写为分数形式.
10. 我们知道分数写为小数形式即 , 反过来,无限循环小数写为分数形式即一般地,任何一个无限循环小数都可以写为分数形式.例:将化为分数形式.
设 , 由可知, , 所以 , 解得于是,得
根据以上阅读,回答下列问题:以下计算结果都用最简分数表示
(1)、【理解】 .(2)、【迁移】将化为分数形式,写出推导过程.温馨提示: , 它的循环节有两 位哦(3)、【创新】若 , 则 .11. 已知一列,数 , , , …,具有以下规律: , .例:若 , 则 , ,
, ,
, …
请认真阅读上面的运算推理过程,完成下面问题.
(1)、若 , 求下列两个问题.① , .
②在数轴上点A所表示的数为 , 点B所表示的数为 , 求线段AB的长.
(2)、已知 , 求的值.12. 【阅读理解】射线是内部的一条射线,若 , 则我们称射线是射线的“友好线”例如,如图 , , , 则 , 称射线是射线的友好线;同时,由于 , 称射线是射线的友好线.【知识运用】
 (1)、如图 , , 射线是射线的友好线,则为多少度;(2)、如图 , , 射线与射线重合,并绕点以每秒的速度逆时针旋转,射线与射线重合,并绕点以每秒的速度顺时针旋转,当射线与射线重合时,运动停止;
(1)、如图 , , 射线是射线的友好线,则为多少度;(2)、如图 , , 射线与射线重合,并绕点以每秒的速度逆时针旋转,射线与射线重合,并绕点以每秒的速度顺时针旋转,当射线与射线重合时,运动停止;①是否存在某个时刻秒 , 使得的度数是 , 若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线、、中恰好有一条射线是另一条射线的友好线.请直接写出所有答案;
13. 我们知道分数写为小数形式即;反过来,无限循环小数写为分数形式即为 .一般地,任何一个无限循环小数都可以写成一个分数的形式.
例:将化为分数形式.
设 , 由可知, , 所以 , 解得 .
于是得 .
根据以上阅读材料,回答下列问题(以下计算结果都用最简分数表示):
(1)、【理解】 .(2)、【迁移】将化为分数形式,写出推导过程(温馨提示: , 它的循环节有两位).(3)、【创新】若已知 , 则 .14. [阅读理解]射线OC是∠AOB内部的一条射线,若∠COA=∠AOB,则我们称射线OC是射线OA的“友好线”.例如,图1中,AOB=60°,∠AOC= ZCOD=∠BOD= 20°,则∠AOC=∠AOB,称射线OC是射线OA的“友好线”;同时,由于∠BOD=∠AOB,称射线OD是射线OB的“友好线”

[知识运用]
(1)、如图2,∠AOB=120°,射线OM是射线OA的“友好线”,则∠AOM=(2)、如图3,∠AOB=180°,射线OC与射线OA重合,并绕点O以每秒2°的速度逆时针旋转,射线OD与射线OB重合,并绕点O以每秒3°的速度顺时针旋转,当射线OD与射线OA重合时,运动停止.①是否存在某个时刻t(秒),使得∠COD的度数是40° ,若存在,求出t的值,若不存在,请说明理由..
②当t为多少秒时,射线OC,OD,OA中恰好有一条射线是另一条射线的“友好线”。(直接写出答案)
15. 新定义问题如图①,已知 ,在 内部画射线 ,得到三个角,分别为 、 、 .若这三个角中有一个角是另外一个角的2倍,则称射线 为 的“幸运线”.(本题中所研究的角都是大于 而小于 的角.)
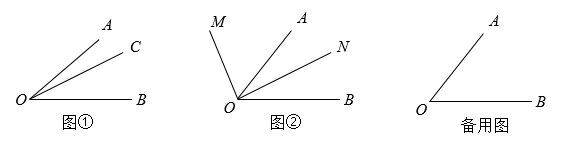 (1)、(阅读理解)
(1)、(阅读理解)角的平分线这个角的“幸运线”;(填“是”或“不是”)
(2)、(初步应用)如图①, ,射线 为 的“幸运线”,则 的度数为;
(3)、(解决问题)如图②,已知 ,射线 从 出发,以每秒 的速度绕 点逆时针旋转,同时,射线 从 出发,以每秒 的速度绕 点逆时针旋转,设运动的时间为 秒( ).若 、 、 三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的 值.
16. 【阅读理解】表示5与2的差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;同理可以理解为与1两数在数轴上所对应的两点之间的距离,就表示在数轴上对应的点到表示的点的距离.
(1)、【尝试应用】①数轴上表示和3的两点之间的距离是(写出最后结果);
②若 , 则;
(2)、【动手探究】伦伦在草稿纸上画了一条数轴,并折叠纸面,若表示的点与表示1的点重合.
①表示的点与数表示的点重合;
②若数轴上、两点之间距离为8(在的左侧),且、两点经折叠后重合,则表示的数是 , 表示的数是;
③若点表示的数为 , 点表示的数为(在的左侧),且 , 两点经折叠刚好重合,那么与之间的数量关系是;
(3)、【拓展延伸】当时,的最小值是 .
17. 【阅读理解】若A , B , C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是的“妙点”。例如,如图1,点A表示的数为 , 点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是的“妙点”.又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是的“妙点”,但点D是的“妙点”.

【知识应用】
如图2,M、N为数轴上两点,点M所表示的数为 , 点N所表示的数为4.
(1)、数3(填“是”或“不是”)的“妙点”,数2(填“是”或“不是”)的“妙点”.(2)、若数轴上有一点Q表示的数是x , 且点Q是的妙点,求x的值.(3)、如图3,A、B为数轴上两点,点A所表示的数为 , 点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止,当t为何值时,点P , A和B中恰有一个点为其余两点的“妙点”?(请直接写出答案)