《图形的初步知识》精选压轴题—浙江省七(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、单选题
-
1. 如图,将两块三角板的直角与的顶点重合在一起,绕点转动三角板 , 使两块三角板仍有部分重叠,且 , 则的度数为( )
 A、 B、 C、 D、2. 如图,点A,O,E在一条直线上,CO与AE互相垂直, , 则下列说法中正确的所有选项是( )
A、 B、 C、 D、2. 如图,点A,O,E在一条直线上,CO与AE互相垂直, , 则下列说法中正确的所有选项是( )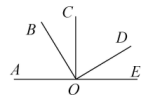
①;
②;
③;
④;
⑤.
A、①②③ B、①③④ C、①③⑤ D、①③④⑤二、填空题
-
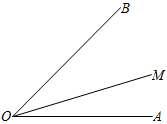
3. 如图,已知 , 射线从出发,以每秒的速度在内部绕点逆时针旋转,若和中,有一个角是另一个角的2倍,则运动时间为秒.
 4. 如图①,点C在线段AB上,图中有三条线段AB、AC和BC , 在这三条线段中,若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”,如图②,点A和B在数轴上表示的数分别是﹣10和26,点C是线段AB的巧点,则点C在数轴上表示的数为 .
4. 如图①,点C在线段AB上,图中有三条线段AB、AC和BC , 在这三条线段中,若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”,如图②,点A和B在数轴上表示的数分别是﹣10和26,点C是线段AB的巧点,则点C在数轴上表示的数为 . 5. 已知线段 , 相交于点(不与端点重合),平分 , 于点 , 若 , 则的度数为 .6. 如图,直线AB⊥OC于点O , ∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP , 现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E'OF' , 同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P'Q' , 设运动时间为m秒(0≤m≤20),当直线P'Q'平分∠E'OF'时,则∠COP'= .
5. 已知线段 , 相交于点(不与端点重合),平分 , 于点 , 若 , 则的度数为 .6. 如图,直线AB⊥OC于点O , ∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP , 现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E'OF' , 同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P'Q' , 设运动时间为m秒(0≤m≤20),当直线P'Q'平分∠E'OF'时,则∠COP'= .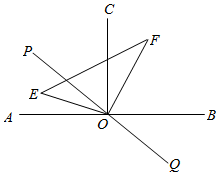 7. 已知 , 射线从与射线重合位置开始绕点O以每秒的速度按顺时针方向旋转,同时射线从与射线重合位置开始绕点O以每秒的速度按逆时针方向旋转,当射线再次与射线重合时.两条射线同时停止旋转,当时,两条射线旋转的时间t的值为 .
7. 已知 , 射线从与射线重合位置开始绕点O以每秒的速度按顺时针方向旋转,同时射线从与射线重合位置开始绕点O以每秒的速度按逆时针方向旋转,当射线再次与射线重合时.两条射线同时停止旋转,当时,两条射线旋转的时间t的值为 . 8. 如图,C是线段AB上的一点,D是BC中点,已知图中所有线段长度之和为23.
8. 如图,C是线段AB上的一点,D是BC中点,已知图中所有线段长度之和为23. (1)、设线段BD的长为x , 则线段AC= . (用含x的代数式表示).(2)、若线段AC , BD的长度都是正整数,则线段AC的长为 .9. 如图,点为线段外一点,点 , , , 为上任意四点,连接 , , , , 下列结论错误的是( )
(1)、设线段BD的长为x , 则线段AC= . (用含x的代数式表示).(2)、若线段AC , BD的长度都是正整数,则线段AC的长为 .9. 如图,点为线段外一点,点 , , , 为上任意四点,连接 , , , , 下列结论错误的是( ) A、以为顶点的角共有15个 B、若 , , 则 C、若为中点,为中点,则 D、若平分 , 平分 , , 则
A、以为顶点的角共有15个 B、若 , , 则 C、若为中点,为中点,则 D、若平分 , 平分 , , 则三、解答题
-
10. 如图 1,把一副三角板拼在一起,边 放在直线 上,其中 , .
 (1)、求图 1 中的度数;(2)、如图 2,三角板固定不动,将三角板绕点 O 顺时针旋转一个角度,在转动过程中,三角板一直在直线 上方,设 .
(1)、求图 1 中的度数;(2)、如图 2,三角板固定不动,将三角板绕点 O 顺时针旋转一个角度,在转动过程中,三角板一直在直线 上方,设 .①若 平分 , 求α;
②若 , 求α.
11. 如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. (1)、如图2,将图1中的三角板绕点O逆时针方向旋转60°至图2的位置,求∠MOC的度数;(2)、如图3,将图1中的三角板绕点O按每秒10°的速度逆时针方向旋转α度(0<α<360°).
(1)、如图2,将图1中的三角板绕点O逆时针方向旋转60°至图2的位置,求∠MOC的度数;(2)、如图3,将图1中的三角板绕点O按每秒10°的速度逆时针方向旋转α度(0<α<360°).①若经过t秒后线段ON在∠AOC的内部,且∠AOM=3∠NOC,求t的值;
②在三角板转动时,射线OC同时绕点O以每秒4°的速度按顺时针方向旋转,当三角板停止转动时,射线OC也停止转动.经过t秒直线ON恰好平分∠AOC,请直接写出满足条件的t的值.
12. 如图1,在直线上取一点O,向上作一条射线 , 使 , 将一直角三角板的直角顶点放在点O处,一边在射线上,另一边在直线的上方.如图2,将直角三角板绕点O逆时针转动,当与第一次重合时停止. (1)、如图2,时,若和互余,且满足始终在内部,求此时的度数;(2)、如图2,当始终在内部时,猜想与有怎样的数量关系(用含n的等式表示),并说明理由;(3)、如图2,当时,若直角三角板绕点O以每秒的速度沿逆时针方向旋转,与第一次重合时停止,在旋转的过程中,若恰好有 , 旋转的时间是秒.(直接写出结果)13. 【阅读理解】射线OC是内部的一条射线,若 , 则我们称射线OC是射线OA的“友好线”.例如,如图1, , 则 , 称射线OC是射线OA的友好线;同时,由于 , 称射线OD是射线OB的友好线.
(1)、如图2,时,若和互余,且满足始终在内部,求此时的度数;(2)、如图2,当始终在内部时,猜想与有怎样的数量关系(用含n的等式表示),并说明理由;(3)、如图2,当时,若直角三角板绕点O以每秒的速度沿逆时针方向旋转,与第一次重合时停止,在旋转的过程中,若恰好有 , 旋转的时间是秒.(直接写出结果)13. 【阅读理解】射线OC是内部的一条射线,若 , 则我们称射线OC是射线OA的“友好线”.例如,如图1, , 则 , 称射线OC是射线OA的友好线;同时,由于 , 称射线OD是射线OB的友好线.【知识运用】
 (1)、如图2, , 射线OM是射线OA的友好线,则为多少度;(2)、如图3, , 射线OC与射线OA重合,并绕点以每秒的速度逆时针旋转,射线OD与射线OB重合,并绕点以每秒的速度顺时针旋转,当射线OD与射线OA重合时,运动停止;
(1)、如图2, , 射线OM是射线OA的友好线,则为多少度;(2)、如图3, , 射线OC与射线OA重合,并绕点以每秒的速度逆时针旋转,射线OD与射线OB重合,并绕点以每秒的速度顺时针旋转,当射线OD与射线OA重合时,运动停止;①是否存在某个时刻t(秒),使得∠COD的度数是 , 若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线OC、OD、OA中恰好有一条射线是另一条射线的友好线.
14. 如图1,将两块直角三角板(一块含有、角,另一块含角)摆放在直线上,三角板绕点以每秒的速度逆时针旋转.当第一次与射线重合时三角板停止转动,设旋转时间为秒.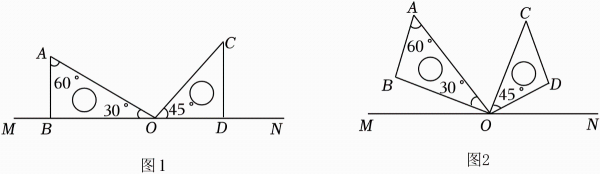 (1)、当时,求和的度数;(2)、如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.
(1)、当时,求和的度数;(2)、如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.①用含的代数式表示射线和射线重合前和的度数;
②整个旋转过程中,当满足时,求出相应的的值.
15. 如果两个角之差的绝对值等于60°,则称这两个角互为等差角.即若 , 则称和互为等差角.(本题中所有角都是指大于0°,且小于180°的角)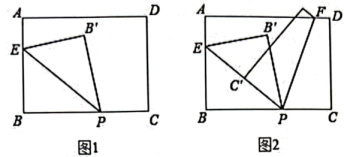 (1)、若和互为等差角.当 , 则 . 当 , 则 .(2)、如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为等差角,求的度数.(3)、再将纸片沿着FP对折(点F在线段CD或AD上)使点C落在点 . 如图2,若点E, , P在同一直线上,且与互为等差角,求的度数.(对折时,线段落在内部)16. 已知:射线OD在内部,.
(1)、若和互为等差角.当 , 则 . 当 , 则 .(2)、如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为等差角,求的度数.(3)、再将纸片沿着FP对折(点F在线段CD或AD上)使点C落在点 . 如图2,若点E, , P在同一直线上,且与互为等差角,求的度数.(对折时,线段落在内部)16. 已知:射线OD在内部,. (1)、如图1,求证:;(2)、如图2,作OF平分∠AOB,求证:;(3)、如图3,在(2)的条件下,当∠AOD=90°时,作射线OA的反向延长线OC,OH在OA的下方,且∠AOH=∠AOE,反向延长射线OE得到射线OQ,射线OP在∠HOQ内部,OG是∠EOP的平分线,若∠BOC-∠DOF=26°,5∠GOH-2∠POQ-∠EOF=71°,求∠BOP的度数.17. 定义:若线段上的一个点把这条线段分成的两条线段,则称这个点是这条线段的三等分点.
(1)、如图1,求证:;(2)、如图2,作OF平分∠AOB,求证:;(3)、如图3,在(2)的条件下,当∠AOD=90°时,作射线OA的反向延长线OC,OH在OA的下方,且∠AOH=∠AOE,反向延长射线OE得到射线OQ,射线OP在∠HOQ内部,OG是∠EOP的平分线,若∠BOC-∠DOF=26°,5∠GOH-2∠POQ-∠EOF=71°,求∠BOP的度数.17. 定义:若线段上的一个点把这条线段分成的两条线段,则称这个点是这条线段的三等分点.
图1 图2
(1)、如图1,点是线段的一个三等分点,满足 , 若 , 则 .(2)、如图2,已知 , 点从点出发,点从点出发,两点同时出发,都以每秒的速度沿射线方向运动秒.①当为何值时,点是线段的三等分点.
②在点 , 点开始出发的同时,点也从点出发,以每秒的速度沿射线方向运动,在运动过程中,点 , 点分别是 , 的三等分点,请直接写出的值.
18. 如果两个角之差的绝对值等于 , 则称这两个角互为等差角,即若 , 则称和互为等差角本题中所有角都是指大于 , 且小于的角 (1)、若和互为等差角当 , 则 当 , 则 ;(2)、如图 , 将一长方形纸片沿着对折点在线段上,点在线段上使点落在点若与互为等差角,求的度数;(3)、再将纸片沿着对折点在线段或上使点落在点如图 , 若点 , , 在同一直线上,且与互为等差角,求的度数对折时,线段落在内部 .19. 新定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.
(1)、若和互为等差角当 , 则 当 , 则 ;(2)、如图 , 将一长方形纸片沿着对折点在线段上,点在线段上使点落在点若与互为等差角,求的度数;(3)、再将纸片沿着对折点在线段或上使点落在点如图 , 若点 , , 在同一直线上,且与互为等差角,求的度数对折时,线段落在内部 .19. 新定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.
如图1,若射线、在的内部,且 , 则是的内半角.
根据以上信息,解决下面的问题:
(1)、如图1, , 若是的内半角,则°;(2)、如图2,已知 , 将绕点O按顺时针方向旋转一个角度()至 . 若是的内半角,求的值;(3)、把一块含有30°角的三角板按图3方式放置.使边与边重合,边与边重合.如图4,将三角板绕顶点O以3度/秒的速度按顺时针方向旋转一周,旋转时间为t秒,当射线、、、构成内半角时,直接写出t的值.20. 定义:同一平面内有若干条以点为端点,且不共线的射线,求出任意两射线间小于 180°的角度 ,并把所有这些角的度数和记为T. 例如:如图1,同一平面内有三条射线 , , , , 是内任意一条射线,则 . (1)、如图2,射线 , , , 在同一平面内绕点O顺时针排列,其中 ,求T的值.(2)、如图3,射线 , , , , 在同一平面内绕点O顺时针排列,其中是(小于 ) 的角平分线,平分 , 且 , ,求的度数.(3)、射线 , , , 在同一平面内,其中 , 比大 , , 直接写出的度数(写出三个即可).
(1)、如图2,射线 , , , 在同一平面内绕点O顺时针排列,其中 ,求T的值.(2)、如图3,射线 , , , , 在同一平面内绕点O顺时针排列,其中是(小于 ) 的角平分线,平分 , 且 , ,求的度数.(3)、射线 , , , 在同一平面内,其中 , 比大 , , 直接写出的度数(写出三个即可).