综合与实践题—浙江省八(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、综合与实践题
-
1. 根据表中素材,探索完成以下任务:
建设“美丽乡村”,落实“乡村振兴”
问题情境
素材1
已知甲、乙两仓库分别有水泥40吨和60吨.
素材2
现在A村需要水泥48吨,B村需要水泥52吨.
素材3
从甲仓库往A,B两村运送水泥的费用分别为20元/吨和25元/吨;
从乙仓库往A,B两村运送水泥的费用分别为15元/吨和24元/吨.
问题解决
分析
设从甲仓库运往A村水泥x吨,补全以下表格.
运量(吨)
运费(元)
甲仓库
乙仓库
甲仓库
乙仓库
A村
x
B村
① ▲
② ▲
问题1
设总运费为y元,请写出y与x的函数关系式并求出最少总运费.
问题2
为了更好地支援乡村建设,甲仓库运往A村的运费每吨减少元,这时甲仓库运往A村的水泥多少吨时总运费最少?最少费用为多少元?(用含a的代数式表示)
2. 现有斜边相等的一副三角板,已知 , .某学习小组利用这副三角板进行数学探究时发现:若这副三角板按如图①或图②方式摆放,连结PC,则PA、PB与PC之间存在一定的数量关系. (1)、聪明的小嘉同学对图①开展了探究,他的思路:通过延长PA至点 , 使得 , 连结CM.然后证明 , 再证是等腰直角三角形,从而获得 , 请你按照小嘉的思路写出完整的解题过程;(2)、若这副三角板按图②方式摆放,则上述PA、PB与PC之间的数量关系还成立吗?若不成立,请写出它们之间存在的数量关系,并说明理由.3. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.
(1)、聪明的小嘉同学对图①开展了探究,他的思路:通过延长PA至点 , 使得 , 连结CM.然后证明 , 再证是等腰直角三角形,从而获得 , 请你按照小嘉的思路写出完整的解题过程;(2)、若这副三角板按图②方式摆放,则上述PA、PB与PC之间的数量关系还成立吗?若不成立,请写出它们之间存在的数量关系,并说明理由.3. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.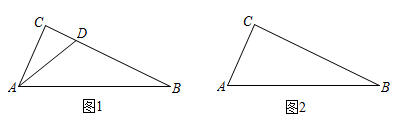 (1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.4. 【问题背景】
(1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.4. 【问题背景】 (1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
(1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
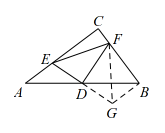
如图2,在等腰中,是底边上的高线,点E为内一点,连接 , 延长到点F,使 , 连接 , 若 , 若 , , 求的长;(3)、【拓展创新】
如图3,在等腰中, , , 点D为中点,点E在线段上(点E不与点B,点D重合),连接 , 过点A作 , 连接 , 若 , , 请直接写出的长.5. 如图1,在中, , D是的中点,点E在线段上,连结 , 作交直线于点F,连结. (1)、【初步尝试】
(1)、【初步尝试】如图2,当 , 线段的长度是 , 线段的长度是.
(2)、【结论探究】如图1,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明.
如图,延长至G,使 , 连结 , .
 (3)、【拓展应用】
(3)、【拓展应用】如图3,当点E在线段的延长线上时,连结 , 作交直线于点F,连结.请补全图形,并求出当时,线段的长.
6. 定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形. (1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .7. 如图,在直角坐标系中,已知点 , 直线l是第二、四象限的角平分线.
(1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .7. 如图,在直角坐标系中,已知点 , 直线l是第二、四象限的角平分线. (1)、操作:连结线段 , 作出线段关于直线l的轴对称图形 .(2)、发现:请写出坐标平面内任一点关于直线l的对称点的坐标.(3)、应用:请在直线l上找一点Q,使得最小,并写出点Q的坐标.8. 综合与实践
(1)、操作:连结线段 , 作出线段关于直线l的轴对称图形 .(2)、发现:请写出坐标平面内任一点关于直线l的对称点的坐标.(3)、应用:请在直线l上找一点Q,使得最小,并写出点Q的坐标.8. 综合与实践生活中的数学:如何确定单肩包最佳背带长度
素材1
如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).

素材2
对于该背包的背带长度进行测量,设双层的部分长度是 , 单层部分的长度是 , 得到如下数据:
双层部分长度
2
6
10
14
单层部分长度
116
108
100
92
70
素材3
单肩包的最佳背带总长度与身高比例为
素材4
小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为;已知爸爸的臂展和身高一样,且肩宽为 , 头顶到肩膀的垂直高度为总身高的 .
 (1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围.
(1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围. (2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.9.
(2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.9.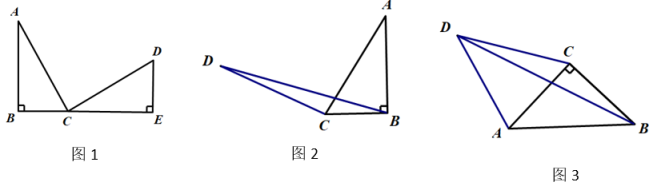 (1)、【问题发现】
(1)、【问题发现】如图1,在△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=4,ED=3,则BE=.
(2)、【问题提出】如图2,在Rt△ABC中,∠ABC=90°,BC=3,过点C作CD⊥AC,且CD=AC,求△BCD的面积.
(3)、【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为14且CD的长为7,求△BCD的面积.
10. (1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:
(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,是的中点, , , A , 三点共线.
求证: .
小明在组内经过合作交流,得到解决方法:延长至点 , 使得 , 连结 .
请根据小明的方法思考:由已知和作图能得到 , 依据是( )
A、 B、 C、 D、(2)、由全等三角形、等腰三角形的性质可得 .
【初步运用】如图2,在中,平分 , 为的中点,过点作 , 分别交的延长线和于点、点A . 求证: .(3)、【拓展运用】如图3,在(1)的基础上(即是的中点, , , A , 三点共线),连结 , 若 , 当 , 时,求的长.11. 我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点. (1)、特例感知
(1)、特例感知①等腰直角三角形 ▲ 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知为勾股高三角形,其中C为勾股顶点,是边上的高.若 , 试求线段的长度.
(2)、深入探究如图2,已知为勾股高三角形,其中C为勾股顶点且 , 是边上的高,试探究线段与的数量关系,并给予证明;
(3)、推广应用如图3,等腰为勾股高三角形,其中 , 为边上的高,过点D向边引平行线与边交于点E . 若 , 试求线段的长度.
12. 综合与实践:数学课上,白老师出示了一个问题:已知等腰直角和等腰直角 , , , , 连接 , , 如图1.
独立思考:
 (1)、如图1,求证:;
(1)、如图1,求证:;实践探究:在原有条件不变的情况下,白老师把旋转到了特殊位置,增加了新的条件,并提出了新的问题,请你解答:
(2)、如图2,在绕着点C旋转到某一位置时恰好有 , .①求的度数;
②线段与线段交于点F , 求的值;
③若 , 求的值.
13. 如图 (1)、问题背景: 如图 1, 在 与 中, .求证: .(2)、类比探究: 如图 2, 在 Rt 中, , 点 为边 B C上任意一点(不是 B C 中点), 求证: .(3)、拓展应用: 如图 3, 在四边形 A B C D 中, , 求 B D 的长.
(1)、问题背景: 如图 1, 在 与 中, .求证: .(2)、类比探究: 如图 2, 在 Rt 中, , 点 为边 B C上任意一点(不是 B C 中点), 求证: .(3)、拓展应用: 如图 3, 在四边形 A B C D 中, , 求 B D 的长.