《特殊三角形》精选压轴题—浙江省八(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、单选题
-
1. 如下图,点在等边的边上, , 射线垂足为点 , 点是射线上一动点,点是线段上一动点,当的值最小时, , 则的长为( )
 A、17 B、16 C、13 D、122. 如图,在“V”字形图形中, , , , , , 若要求出这个图形的周长,则需添加的一个条件是( ).
A、17 B、16 C、13 D、122. 如图,在“V”字形图形中, , , , , , 若要求出这个图形的周长,则需添加的一个条件是( ). A、的长 B、的长 C、的长 D、与的和3. 如图,将一张直角梯形纸板( , )剪成3部分,恰好能拼成一个等腰三角形.若想知道1号部分的周长,则只需测量下列哪条线段即可( )
A、的长 B、的长 C、的长 D、与的和3. 如图,将一张直角梯形纸板( , )剪成3部分,恰好能拼成一个等腰三角形.若想知道1号部分的周长,则只需测量下列哪条线段即可( )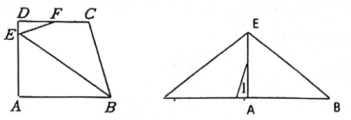 A、 B、 C、 D、4. 如图,将一张直角梯形纸板( , )剪成3部分,恰好能拼成一个等腰三角形,若想知道1号部分的周长,则只需测量下列哪条线段即可( )
A、 B、 C、 D、4. 如图,将一张直角梯形纸板( , )剪成3部分,恰好能拼成一个等腰三角形,若想知道1号部分的周长,则只需测量下列哪条线段即可( )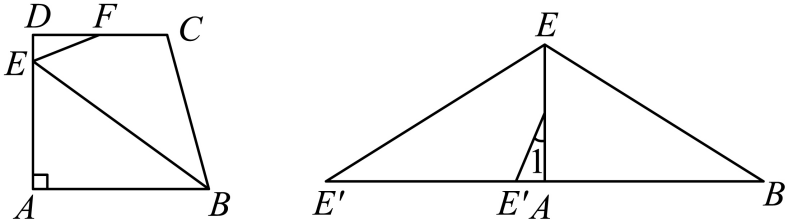 A、 B、 C、 D、5. 如图,在中, , , , 以其三边为边向形外分别作正方形,然后将整个图形放置于如图所示的长方形中,使点D,E,F,G,H恰好在长方形的边上,则图中阴影部分的面积为( ).
A、 B、 C、 D、5. 如图,在中, , , , 以其三边为边向形外分别作正方形,然后将整个图形放置于如图所示的长方形中,使点D,E,F,G,H恰好在长方形的边上,则图中阴影部分的面积为( ). A、 B、 C、56 D、6. 如图,在△ABC中,AB=AC=16,BC=12,AF⊥BC于点F , BE⊥AC于点E , D为AB的中点,M为EF的中点,则DM的长为( )
A、 B、 C、56 D、6. 如图,在△ABC中,AB=AC=16,BC=12,AF⊥BC于点F , BE⊥AC于点E , D为AB的中点,M为EF的中点,则DM的长为( )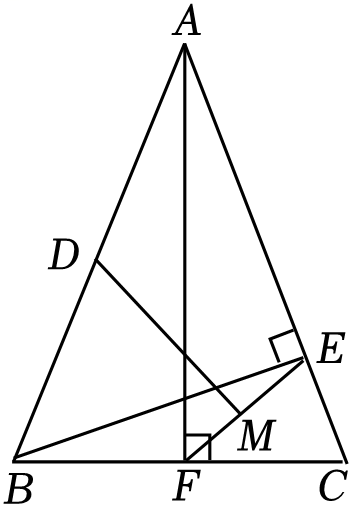 A、7 B、8 C、 D、7. 如图,等边中,D、E分别为AC、BC边上的点, , 连接AE、BD交于点的平分线交于AC边上的点G,BG与AE交于点 , 连接FG.下列说法:
A、7 B、8 C、 D、7. 如图,等边中,D、E分别为AC、BC边上的点, , 连接AE、BD交于点的平分线交于AC边上的点G,BG与AE交于点 , 连接FG.下列说法:
①;②;③;④AB=AH+FG;
其中正确的说法是( )
A、4个 B、3个 C、2个 D、1个8. 如图,在中, , , , 点为上一点,点分别是点关于的对称点,则的最小值是( ) A、 B、 C、4 D、29. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )
A、 B、 C、4 D、29. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( ) A、①②④ B、①②③ C、③④ D、①②③④
A、①②④ B、①②③ C、③④ D、①②③④二、填空题
-
10. 如图,等腰中, , , 为内一点,且 , , 则.
 11. 已知,在中, , 点D在斜边上,将沿着过点D的一条直线翻折,使点B落在射线上的处,连结 .(1)、当D是的中点时, .(2)、当△是直角三角形时,的长是 .12. 如图, , 已知中, , , 的顶点A、B分别OM、ON上,当点B在边ON上运动时,A随之在边OM上运动,的形状始终保持不变,在运动的过程中,点C到点O的最小距离为 .
11. 已知,在中, , 点D在斜边上,将沿着过点D的一条直线翻折,使点B落在射线上的处,连结 .(1)、当D是的中点时, .(2)、当△是直角三角形时,的长是 .12. 如图, , 已知中, , , 的顶点A、B分别OM、ON上,当点B在边ON上运动时,A随之在边OM上运动,的形状始终保持不变,在运动的过程中,点C到点O的最小距离为 . 13. 如图,在中, , , D是AB上一点,且 , E是BC上一点,把沿DE翻折得 , 线段与BC交于点F,当所在的直线与的一边垂直时,DF的长是 .
13. 如图,在中, , , D是AB上一点,且 , E是BC上一点,把沿DE翻折得 , 线段与BC交于点F,当所在的直线与的一边垂直时,DF的长是 . 14. 如图,已知在Rt△ABC中, , , , 点D,E分别在边上,连接 , , 将沿翻折,将沿翻折,翻折后,点B,C分别落在点 , 处,且边与在同一条直线上,连接 , 当△ADC’是以为腰的等腰三角形时,则BD= .
14. 如图,已知在Rt△ABC中, , , , 点D,E分别在边上,连接 , , 将沿翻折,将沿翻折,翻折后,点B,C分别落在点 , 处,且边与在同一条直线上,连接 , 当△ADC’是以为腰的等腰三角形时,则BD= . 15. 如图,在△ABC中,AB=AC,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点.
15. 如图,在△ABC中,AB=AC,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点. (1)、若△DEF的周长是8,则△ABC的周长是 ;(2)、若AE:EC=3:2,则AF:EF= .16. 如图,在等边 中, ,点O在线段 上,且 ,点 是线段 上一点,连接 ,以 为圆心, 长为半径画弧交线段 于一个点 ,连接 ,如果 ,那么 的长是 .
(1)、若△DEF的周长是8,则△ABC的周长是 ;(2)、若AE:EC=3:2,则AF:EF= .16. 如图,在等边 中, ,点O在线段 上,且 ,点 是线段 上一点,连接 ,以 为圆心, 长为半径画弧交线段 于一个点 ,连接 ,如果 ,那么 的长是 .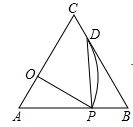 17. 如图,在长方形中,为等腰△,且 , 点在线段上,点在线段上,若 , 则 .
17. 如图,在长方形中,为等腰△,且 , 点在线段上,点在线段上,若 , 则 . 18. 如图,有一直角三角形纸片 , , , , 于点 . , 分别是线段 , 上的点, , Ⅰ分别是线段 , 上的点,沿 , 折叠,使点 , 恰好都落在线段上的点处.当时,的长是 .
18. 如图,有一直角三角形纸片 , , , , 于点 . , 分别是线段 , 上的点, , Ⅰ分别是线段 , 上的点,沿 , 折叠,使点 , 恰好都落在线段上的点处.当时,的长是 . 19. 如图,在中, , , 点在上且 , 点是上的动点,连结 , 点分别是和的中点,连结 . 当时,线段的长为 .
19. 如图,在中, , , 点在上且 , 点是上的动点,连结 , 点分别是和的中点,连结 . 当时,线段的长为 . 20. 如图,中, , 点D是上一动点,将沿折叠得到 , 当与重叠部分是直角三角形时,的度数为 .
20. 如图,中, , 点D是上一动点,将沿折叠得到 , 当与重叠部分是直角三角形时,的度数为 . 21. 如图,边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,连结AF并延长交BC于点M . 若AH=HE , 则CM的长为 .
21. 如图,边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,连结AF并延长交BC于点M . 若AH=HE , 则CM的长为 .
三、解答题
-
22. 已知和都是等腰直角三角形,且.
 (1)、如图1,点D在内,求证:;(2)、如图2,A、D、E三点在同一条直线上,若 , , 求的面积;(3)、如图3,若 , 点D在边上运动,求周长的最小值.23. 在四边形中, , , , 为中点,连接 , 交于点 .
(1)、如图1,点D在内,求证:;(2)、如图2,A、D、E三点在同一条直线上,若 , , 求的面积;(3)、如图3,若 , 点D在边上运动,求周长的最小值.23. 在四边形中, , , , 为中点,连接 , 交于点 . (1)、当时, , ;(2)、当的大小改变时,的度数是否发生改变?若变化,求的变化范围,若不变,求的度数;(3)、猜想 , , 之间的数量关系,并说明理由;(4)、若 , 则 .24. 如图(1),是的边上的中线,将沿直线翻折得到 , 连接 , .
(1)、当时, , ;(2)、当的大小改变时,的度数是否发生改变?若变化,求的变化范围,若不变,求的度数;(3)、猜想 , , 之间的数量关系,并说明理由;(4)、若 , 则 .24. 如图(1),是的边上的中线,将沿直线翻折得到 , 连接 , . (1)、求证:是直角三角形.(2)、如图(2),若 , , 求的大小.(3)、若是直角三角形,是等边三角形,探究与的数量关系.
(1)、求证:是直角三角形.(2)、如图(2),若 , , 求的大小.(3)、若是直角三角形,是等边三角形,探究与的数量关系.四、实践探究题
-
25. 定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形.
 (1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .26. 综合与实践:
(1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .26. 综合与实践:数学课上,白老师出示了一个问题:已知等腰直角和等腰直角 , , , , 连接 , , 如图1.
独立思考:
 (1)、如图1,求证:;
(1)、如图1,求证:;实践探究:在原有条件不变的情况下,白老师把旋转到了特殊位置,增加了新的条件,并提出了新的问题,请你解答:
(2)、如图2,在绕着点C旋转到某一位置时恰好有 , .①求的度数;
②线段与线段交于点F , 求的值;
③若 , 求的值.
27. 定义:把斜边重合,且直角顶点不重合 两个直角三角形叫做共边直角三角形.
两个直角三角形叫做共边直角三角形.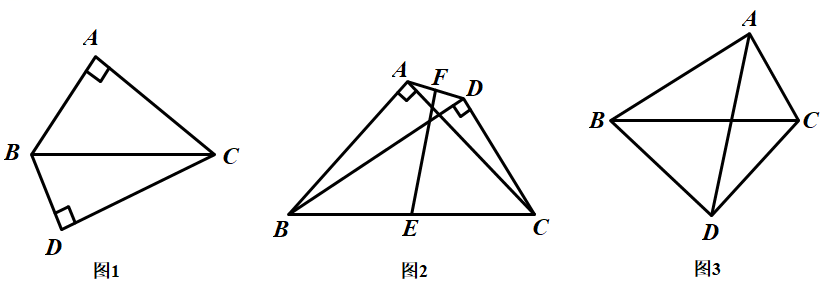 (1)、概念理解:如图1,在和中, , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是、的中点,连结 , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连结 , 求证:平分 .28.
(1)、概念理解:如图1,在和中, , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是、的中点,连结 , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连结 , 求证:平分 .28. (1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:
(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,是的中点, , , A , 三点共线.
求证: .
小明在组内经过合作交流,得到解决方法:延长至点 , 使得 , 连结 .
请根据小明的方法思考:由已知和作图能得到 , 依据是( )
A、 B、 C、 D、(2)、由全等三角形、等腰三角形的性质可得 .
【初步运用】如图2,在中,平分 , 为的中点,过点作 , 分别交的延长线和于点、点A . 求证: .(3)、【拓展运用】如图3,在(1)的基础上(即是的中点, , , A , 三点共线),连结 , 若 , 当 , 时,求的长.