《三角形的全等》精选压轴题—浙江省八(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、单选题
-
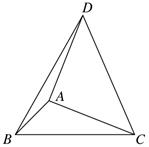
1. 如图,在△ABC中,∠ABC=45° , BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .
 A、8 B、10 C、4 D、82. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC
A、8 B、10 C、4 D、82. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF; ②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE
④.若BE平分∠ABC,则FG=;
 A、①②③ B、③④ C、①②④ D、①②③④3. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )
A、①②③ B、③④ C、①②④ D、①②③④3. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )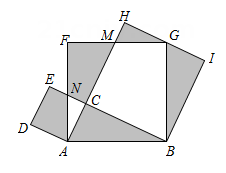 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
4. 在平面直角坐标系中,已知点 , 点是线段上一点,交轴于 , 且 ,
 (1)、的坐标为: .(2)、若为射线上一点,且 , 则点的坐标为 .5. 直线CD经过∠BCA的顶点C , CA=CB . E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
(1)、的坐标为: .(2)、若为射线上一点,且 , 则点的坐标为 .5. 直线CD经过∠BCA的顶点C , CA=CB . E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则EF|BE﹣AF|(填“>”,“<”或“=”号);
②如图2,若0°<∠BCA<180°,若使①中的结论仍然成立,则∠α与∠BCA应满足的关系是 .
6. 如图,在中, , , 点是外角平分线上的一点,连接、 , 若 , 则度. 7. 在直角三角形纸片中, , 折叠纸片使得点落在边上点处,折痕是(如图1),将纸片复原,再次折叠纸片,使得点落在边上的点处,折痕是(如图2),继续折叠纸片,使得点与点重合,折痕是 , 得到多边形(如图3).将若干个全等的多边形交叉重叠便可得到棒棒糖的糖果部分(如图4).
7. 在直角三角形纸片中, , 折叠纸片使得点落在边上点处,折痕是(如图1),将纸片复原,再次折叠纸片,使得点落在边上的点处,折痕是(如图2),继续折叠纸片,使得点与点重合,折痕是 , 得到多边形(如图3).将若干个全等的多边形交叉重叠便可得到棒棒糖的糖果部分(如图4).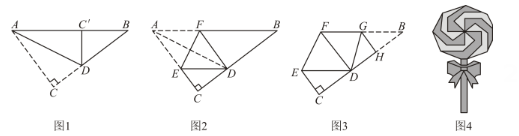 (1)、图1中的长为 .(2)、图3中的长为 .8. 如图1,在 中, , 为 中点.将 沿 翻折,得到 (如图2), 为 上一点,再将 沿 翻折,使得 与 重合(如图3),给出下列四个命题:① ;② ;③ ;④ .其中说法正确的是.
(1)、图1中的长为 .(2)、图3中的长为 .8. 如图1,在 中, , 为 中点.将 沿 翻折,得到 (如图2), 为 上一点,再将 沿 翻折,使得 与 重合(如图3),给出下列四个命题:① ;② ;③ ;④ .其中说法正确的是.

 9. 在平面直角坐标系中 , , 过点B作直线lx轴,点是线l上的动点,以AP为边在AP右侧作等腰 , 使∠APQ=90°.
9. 在平面直角坐标系中 , , 过点B作直线lx轴,点是线l上的动点,以AP为边在AP右侧作等腰 , 使∠APQ=90°.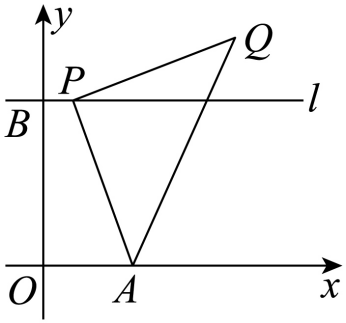 (1)、当a=0时,则点Q的坐标是 .(2)、当点P在直线l上运动时,点Q也随之运动,则OQ的最小值是 .
(1)、当a=0时,则点Q的坐标是 .(2)、当点P在直线l上运动时,点Q也随之运动,则OQ的最小值是 .三、解答题
-
10. 如图1,为等腰直角三角形,∠=90°,动点从出发沿线段向终点运动,连结 , 以为直角边向右作等腰直角△ , 斜边与交于点 , 连结 .
 (1)、求证:△≌△;(2)、如图2,过分别作于点于点 . 请探究:三条线段之间的数量关系;(3)、在(2)的条件下,若AB=2,当等于多少时,的面积最大?并求出最大值.11. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内.
(1)、求证:△≌△;(2)、如图2,过分别作于点于点 . 请探究:三条线段之间的数量关系;(3)、在(2)的条件下,若AB=2,当等于多少时,的面积最大?并求出最大值.11. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内. (1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.12. 在等腰中,是射线上的动点,过点作(始终在上方),且 , 连接 .
(1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.12. 在等腰中,是射线上的动点,过点作(始终在上方),且 , 连接 . (1)、如图1,当点D在线段上时,判断的形状,并说明理由.(2)、如图2,若D , E为线段上的两个动点,且 , 连接 , 求的长.(3)、如图3,若M为中点,连接 , 在点的运动过程中,当时,的长最小,最小值是 .13. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,E,F分别是直线AC,AB上的动点,连结EF.
(1)、如图1,当点D在线段上时,判断的形状,并说明理由.(2)、如图2,若D , E为线段上的两个动点,且 , 连接 , 求的长.(3)、如图3,若M为中点,连接 , 在点的运动过程中,当时,的长最小,最小值是 .13. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,E,F分别是直线AC,AB上的动点,连结EF. (1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.
(1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.四、实践探究题
-
14.
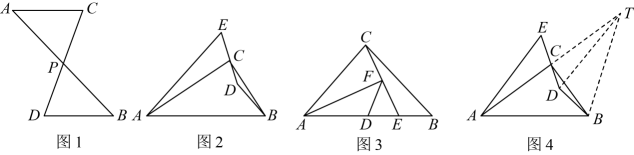 (1)、【思维启迪】
(1)、【思维启迪】如图1,点P是线段 , 的中点,则与的数量关系为 , 位置关系为;
(2)、【思维探索】如图2,在中, , 点D为内一点,连接 , , 延长到点E , 使 , 连接 , 若 , 请用等式表示 , , 之间的数量关系,并说明理由;
★小明思考良久后,根据这一条件,给出了如图4的辅助线:延长到T , 使得 , 连接 , , 请你根据小明给出的辅助线,继续猜想 , , 之间的数量关系,并说明理由.
(3)、如图3,在中, , , 点D为中点,点E在线段上(点E不与点B , 点D重合),连接 , 过点A作 , 连接 , 若 , , 请求出的长.