《一次函数》精选压轴题—浙江省八(上)数学期末复习
试卷更新日期:2025-01-01 类型:复习试卷
一、选择题
-
1. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( )
 A、
A、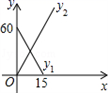 B、
B、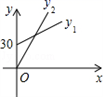 C、
C、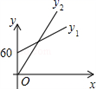 D、
D、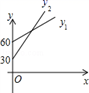 2. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,3. 一次函数的图象与x轴的交点坐标为 , 且 , 则p的取值范围是( )A、 B、 C、 D、4. 如图1,在中, , 点从点出发,沿三角形的边以的速度运动,图2是点运动时,线段的长度随运动时间变化的图象.若点是曲线的最低点,则点的纵坐标为( )
2. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,3. 一次函数的图象与x轴的交点坐标为 , 且 , 则p的取值范围是( )A、 B、 C、 D、4. 如图1,在中, , 点从点出发,沿三角形的边以的速度运动,图2是点运动时,线段的长度随运动时间变化的图象.若点是曲线的最低点,则点的纵坐标为( )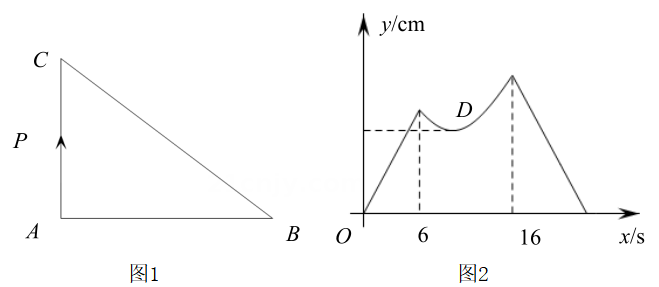 A、 B、4 C、 D、6
A、 B、4 C、 D、6二、填空题
-
5. 图象法是函数的表示方法之一,下面我们就一类特殊的函数图象展开探究.
…
-3
-2
-1
0
1
2
3
…
…
6
4
2
0
2
4
6
…
画函数的图象,经历列表、描点、连线过程得到函数图象如图所示:
探究发现:函数的图象是由向右平移2个单位得到;
函数的图象是由向上平移3个单位得到.
 (1)、函数的最小值为;(2)、函数在中有最小值4,则的值是.6.
(1)、函数的最小值为;(2)、函数在中有最小值4,则的值是.6.如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴于点A3 , …,按此做法进行下去,点An的坐标为
 7. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .8. 已知,一次函数的图象与x轴、y轴分别交于点A、点B,在第一象限内有一点P,使得是等腰直角三角形,则点P的横坐标为.
7. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .8. 已知,一次函数的图象与x轴、y轴分别交于点A、点B,在第一象限内有一点P,使得是等腰直角三角形,则点P的横坐标为.三、解答题
-
9. 小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段与折线分别表示两人离家的距离(km)与小王的行驶时间(h)之间的函数关系的图象,请解决以下问题.
 (1)、求的函数表达式;(2)、求CD的函数表达式;(3)、求点的坐标;(4)、设小王和妈妈两人之间的距离为S(km),当时,求的取值范围.10. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .
(1)、求的函数表达式;(2)、求CD的函数表达式;(3)、求点的坐标;(4)、设小王和妈妈两人之间的距离为S(km),当时,求的取值范围.10. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .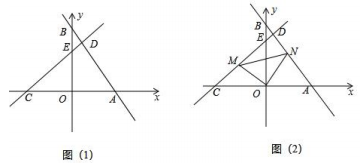 (1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .
(1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .①点M移动过程中,线段与数量关系是否不变,直接写出结论;
②当面积最小时,求点M的坐标和面积.
11. 如图1,点的坐标是 , 垂直于轴于点 , 是直线在第一象限上的动点,交轴于点 . (1)、求当点的坐标为时,
(1)、求当点的坐标为时,①求直线的解析式;
②求的面积;
③为坐标轴上一点,且是以为底边的等腰三角形,请直接写出点的坐标.
(2)、如图2,是线段上一点,且 , 取的中点 , 求的面积.12. 如图,在平面直角坐标系中,点A(0,8),B(﹣4,0),C(4,0),给出如下定义:若P为△ABC内(不含边界)一点,且BP与△APC的一条边相等,则称点P为△ABC的和谐点.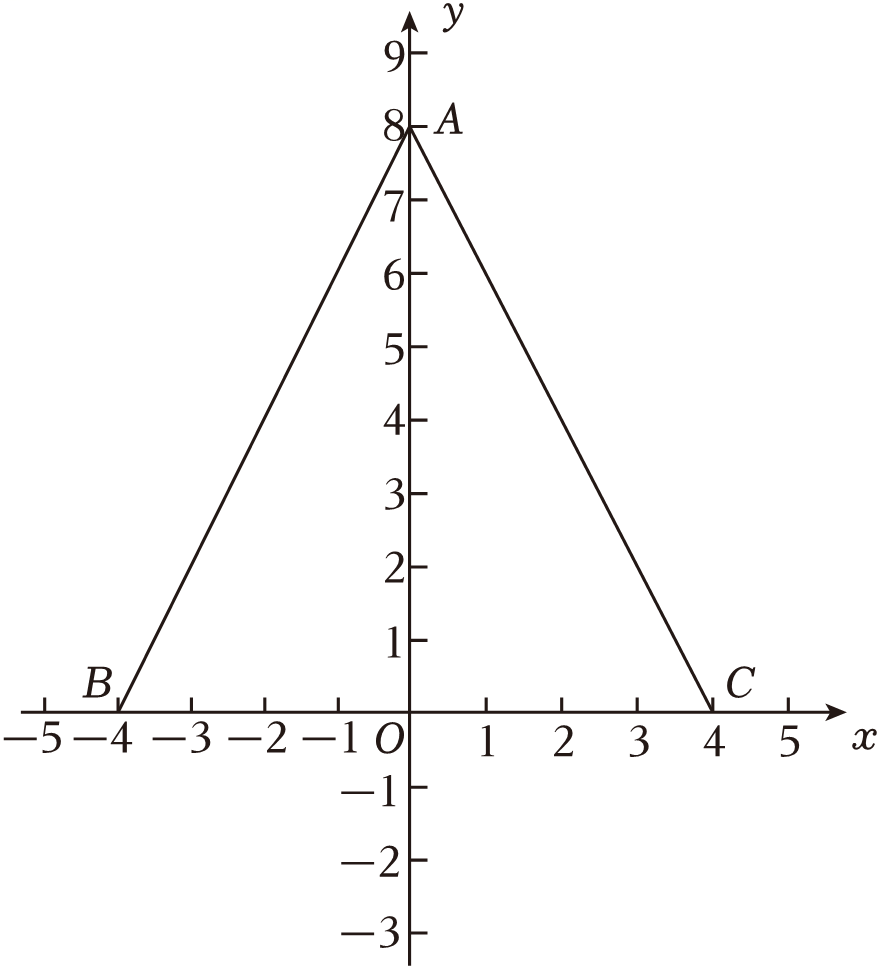 (1)、在P1(﹣1,1),P2(2,2),P3(0,5)中,△ABC的和谐点是 ;(2)、若点P为△ABC的和谐点,且∠ABP=45°,求点P的坐标;(3)、直线l为过点M(0,m)且与x轴平行的直线,若直线l上存在△ABC的二个和谐点,请直接写出m的取值范围.13. 如图,在平面直角坐标系中,直线与x轴和y轴分别交于点B,C,与直线相交于点A.
(1)、在P1(﹣1,1),P2(2,2),P3(0,5)中,△ABC的和谐点是 ;(2)、若点P为△ABC的和谐点,且∠ABP=45°,求点P的坐标;(3)、直线l为过点M(0,m)且与x轴平行的直线,若直线l上存在△ABC的二个和谐点,请直接写出m的取值范围.13. 如图,在平面直角坐标系中,直线与x轴和y轴分别交于点B,C,与直线相交于点A. (1)、求点A的坐标及的面积.(2)、在线段OA上有一动点P,过点P作平行于y轴的直线与直线AC交于点D,问在y轴上是否存在点H,使得是以P为直角顶点的等腰直角三角形?若存在,请求出满足条件的点H的坐标;若不存在,请说明理由.(3)、过点A作y轴的垂线AE,垂足为E,在y轴上找点M,使 , 请直接写出点M的坐标.14. 如图1,直线分别与轴,轴交于点两点,为线段上的动点,点关于直线成轴对称,连结 .
(1)、求点A的坐标及的面积.(2)、在线段OA上有一动点P,过点P作平行于y轴的直线与直线AC交于点D,问在y轴上是否存在点H,使得是以P为直角顶点的等腰直角三角形?若存在,请求出满足条件的点H的坐标;若不存在,请说明理由.(3)、过点A作y轴的垂线AE,垂足为E,在y轴上找点M,使 , 请直接写出点M的坐标.14. 如图1,直线分别与轴,轴交于点两点,为线段上的动点,点关于直线成轴对称,连结 . (1)、求直线的解析式.(2)、如图2,连结并延长交于点 , 若 , 求点的坐标.(3)、如图3,点是的中点,连结 . 当与中的一条边平行时,直接写出的长.15. 已知,如图1,直线AB:y=kx-k-4,分别交平面直角坐标系于A,B两点,直线与坐标轴交于C,D两点,两直线交于点;
(1)、求直线的解析式.(2)、如图2,连结并延长交于点 , 若 , 求点的坐标.(3)、如图3,点是的中点,连结 . 当与中的一条边平行时,直接写出的长.15. 已知,如图1,直线AB:y=kx-k-4,分别交平面直角坐标系于A,B两点,直线与坐标轴交于C,D两点,两直线交于点; (1)、求点的坐标和的值;(2)、如图2,点是轴上一动点,连接ME,将沿ME翻折,当点对应点刚好落在轴上时,求ME所在直线解析式;(3)、在直线AB上是否存在点 , 使得 , 若存在,请求出点坐标,若不存在请说明理由.16. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
(1)、求点的坐标和的值;(2)、如图2,点是轴上一动点,连接ME,将沿ME翻折,当点对应点刚好落在轴上时,求ME所在直线解析式;(3)、在直线AB上是否存在点 , 使得 , 若存在,请求出点坐标,若不存在请说明理由.16. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
 (1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.17. 综合与实践
(1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.17. 综合与实践生活中的数学:如何确定单肩包最佳背带长度
素材1
如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).

素材2
对于该背包的背带长度进行测量,设双层的部分长度是 , 单层部分的长度是 , 得到如下数据:
双层部分长度
2
6
10
14
单层部分长度
116
108
100
92
70
素材3
单肩包的最佳背带总长度与身高比例为
素材4
小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为;已知爸爸的臂展和身高一样,且肩宽为 , 头顶到肩膀的垂直高度为总身高的 .
 (1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围.
(1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围. (2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
(2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.