北师大版数学七年级上学期期末模拟卷（二）

试卷更新日期：2024-12-29 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共36分）

1. 全国两会，习近平总书记在参加江苏代表团审议时指出，我们能不能如期全面建成社会主义现代化强国，关键看科技自立自强．将“科技、自立、自强”六个字分别写在某正方体的表面上，如图是它的一种表面展开图，在原正方体中，与“强”字所在面相对面上的汉字是（）

A、自 B、立 C、科 D、技

查看试题解析
2. 用数轴上的点表示下列各数，其中与原点距离最近的是（）

A、 $- 3$ B、1 C、2 D、3

查看试题解析
3. 新时代十年来，我国建成世界上规模最大的社会保障体系，其中基本医疗保险的参保人数由 $5.4$ 亿增加到 $13.6$ 亿，参保率稳定在 $95 %$ ．将数据 $13.6$ 亿用科学记数法表示为（）

A、 $13.6 \times 10^{8}$ B、 $1.36 \times 10^{8}$ C、 $1.36 \times 10^{9}$ D、 $13.6 \times 10^{9}$

查看试题解析
4. 如果一个数等于它的全部真因数（含单位1，不含它本身）的和，那么这个数称为完美数．例如：6的真因数是1、2、3，且 $6 = 1 + 2 + 3$ ，则称6为完美数．下列数中为完美数的是（）

A、8 B、18 C、28 D、32

查看试题解析
5. 下列运算中，正确的是（　　）

A、3a+2b=5ab B、2a³+3a²=5a⁵ C、3a²b﹣3ba²=0 D、5a²﹣4a²=1

查看试题解析
6. 下列语句准确规范的是（）

A、直线a，b相交于点m B、反向延长线 $A B$ 至点C C、延长射线 $O A$ D、延长线段 $A B$ 至点C，使得 $B C = A B$

查看试题解析
7. 如图，点C是线段AB上一点，点M是AC的中点，点N是BC的中点，如果MC比NC长2cm，AC比BC长（　　）

A、2cm B、4cm C、1cm D、6cm

查看试题解析
8. 若∠A=20°18'，∠B=20°15"，∠C=20.25°，则有（）

A、∠A>∠B>∠C B、∠B>∠A>∠C C、∠A>∠C>∠B D、∠C>∠A>∠B

查看试题解析
9. 如图，∠AOD＝84°，∠AOB＝18°，OB平分∠AOC，则∠COD的度数是（）

A、48° B、42° C、36° D、33°

查看试题解析
10. 解方程 $\frac{1 - y}{3} = \frac{y - 1}{2} - 5$ 时，去分母正确的是（）

A、1-y=y-1-10 B、2（1-y）=3（y-1）-5 C、2（1-y）=3（y-1）-30 D、2（1-y）=3（1-y）+30

查看试题解析
11. 《孙子算经》记载：“今有木，不知长短．引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”（尺、寸是长度单位，1尺＝10寸）．意思是，现有一根长木，不知道其长短．用一根绳子去度量长木，绳子还剩余4.5尺；将绳子对折再度量长木，长木还剩余1尺．问长木长多少？设长木长为x尺，则可列方程为（）

A、 $\frac{1}{2} (x + 4.5) = x - 1$ B、 $\frac{1}{2} (x + 4.5) = x + 1$ C、 $\frac{1}{2} (x - 4.5) = x + 1$ D、 $\frac{1}{2} (x - 4.5) = x - 1$

查看试题解析
12. 以下调查中，适合全面调查的是（）．

A、了解全国中学生的视力情况 B、检测“神舟十六号”飞船的零部件 C、检测台州的城市空气质量 D、调查某池塘中现有鱼的数量

查看试题解析

二、填空题（每题3分，共18分）

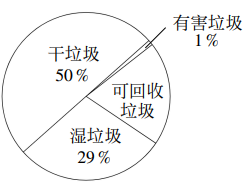
13. 若关于x的方程 $(k - 3) x^{| k - 2 |} + 5 k + 1 = 0$ 是一元一次方程，则k=.

查看试题解析
14. 垃圾分类（Refuse sorting），是指按照垃圾的不同成分、属性、利用价值以及对环境的影响，并根据不同处置方式的要求，分成属性不同的若干种类．某市试点区域的垃圾收集情况如扇形统计图所示，已知可回收垃圾共收集60 吨，且全市人口约为试点区域人口的10倍，那么估计全市可收集的干垃圾总量为．

查看试题解析
15. 小磊在解方程 $\frac{3}{2} （ 1 -$ $\frac{□ - x}{3}) = x - \frac{1}{3}$ 时，墨水把其中一个数字染成了“ $□$ ”，他翻阅了答案，知道这个方程的解为 $x = \frac{2}{3},$ 于是他推算出“ $□$ ”处的数字是.

查看试题解析
16. 若∠MON=80°，P 是平面上一点，且OA 平分∠MOP，OB 平分∠NOP.当射线OP 在∠MON 外部绕点O 旋转时，∠AOB=.

查看试题解析
17. 定义运算： $a ※ b = b - 2 a$ ，下面给出了关于这种运算的四个结论：
① $(- 2) ※ (- 5) = - 1$ ； ② $a ※ b = b ※ a$ ；
③若 $a + b = 0$ ，则 $(a ※ a) + (b ※ b) = 0$ ； ④若 $3 ※ x = 0$ ，则 $x = 6$ ．
其中，正确结论的序号是（填上你认为所有正确结论的序号）．

查看试题解析
18. 中国古代数学著作《增删算法统宗》中记载的“绳索量竿”问题，大意是：现有一根竿子和一条绳索，用绳索去量竿子，绳索比竿子长5尺；若将绳索对折去量竿子，绳索就比竿子短5尺，问绳索、竿子各有多长？该问题中的竿子长为尺．

查看试题解析

三、解答题（共8题，共66分）

19. 计算： $|- 2 - 4| - 32 \div (- 8) \times (- \frac{1}{2})$ ．

查看试题解析
20. 计算： $- 1^{2024} + | - 5 | \times (- \frac{8}{5}) - {(- 4)}^{2} \div (- 8)$

查看试题解析
21. 解方程：

(1)、 $3 (x - 2) + 1 = x - (2 x - 1)$

(2)、 $x - \frac{3 x + 2}{3} = 1 - \frac{x - 2}{2}$

查看试题解析
22. 已知关于x的多项式A，B，其中 $A = m x^{2} + 2 x - 1$ ， $B = x^{2} - n x + 2$ （m，n为有理数）．

(1)、化简 $2 B - A$ ；

(2)、若 $2 B - A$ 的结果不含x项和 $x^{2}$ 项，求 $m - n$ 的值．

查看试题解析
23. 为了解某地区电视观众对新闻、动画、娱乐三类节目的喜爱情况，根据老年人、中年人、青少年各年龄段实际人口的比例，按 $3 : 5 : 2$ 随机抽取一定数量的观众进行调查，得到如下统计图（图一和图二）．

(1)、上面所用的调查方法是________（填“普查”或“抽样调查”）；

(2)、写出折线统计图中A所代表的值是________；

(3)、求该地区被调查的观众中，喜爱娱乐类节目的中年人的人数；

(4)、根据以上统计图提供的信息，请你简要分析该地区电视观众对新闻、动画、娱乐三类节目的喜爱情况．

查看试题解析
24. 元旦节当天，为奖励本学期劳动活动优秀的同学，小明和小红志愿去购买书包作为奖品，根据图中情景，解答下列问题：

(1)、购买 $m$ 个书包需要多少元？（请用含 $m$ 的式子表示）

(2)、小红比小明多买2个书包，付款时小红反而比小明少7元，你认为这种情况可能吗？请利用方程知识说明理由．

查看试题解析
25. 已知∠AOB 与∠COD 有公共顶点O，∠AOB=α，∠COD=β.

(1)、如图①，点A，O，C在一条直线上，若α=60°，β=30°，OM 为∠AOD 的平分线，ON 为∠COB 的平分线，求∠MON 的度数.

(2)、若α=2β，∠AOB，∠COD 绕点O 旋转到如图②所示的位置，OE 为∠BOD 的平分线，用等式表示∠AOD 与∠COE 之间的数量关系，并说明理由.

查看试题解析
26. 如图，数轴上A，B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．

(1)、当0＜t＜5时，用含t的式子填空：
BP＝， AQ＝；

(2)、当t＝2时，求PQ的值；

(3)、当PQ＝ $\frac{1}{2}$ AB时，求t的值．

查看试题解析