2025高考一轮复习(人教A版)第二十二讲空间直线、平面平行的判定和性质
试卷更新日期:2024-12-22 类型:一轮复习
一、选择题
-
1. 已知为直线的方向向量,分别为平面的法向量(不重合),则下列说法中,正确的是( )A、 B、 C、 D、2. 如图,若是棱长为2的正方体的表面上一个动点,则下列结论正确的是( )
 A、当在平面内运动时,四棱锥的体积变化. B、若是棱的中点,当在底面ABCD内运动,且满足平面时,PF长度的最小值是 C、使直线AP与平面ABCD所成的角为的点的轨迹长度为 D、当在线段AC上运动时,与所成角的取值范围是3. 在空间四边形中,分别为边上的点,且 , 又分别为的中点,则( )A、平面 , 且四边形是矩形 B、平面 , 且四边形是梯形 C、平面 , 且四边形是菱形 D、平面 , 且四边形是平行四边形4. 如图,为平行四边形所在平面外一点,为的中点,为上一点,当∥平面时,( )
A、当在平面内运动时,四棱锥的体积变化. B、若是棱的中点,当在底面ABCD内运动,且满足平面时,PF长度的最小值是 C、使直线AP与平面ABCD所成的角为的点的轨迹长度为 D、当在线段AC上运动时,与所成角的取值范围是3. 在空间四边形中,分别为边上的点,且 , 又分别为的中点,则( )A、平面 , 且四边形是矩形 B、平面 , 且四边形是梯形 C、平面 , 且四边形是菱形 D、平面 , 且四边形是平行四边形4. 如图,为平行四边形所在平面外一点,为的中点,为上一点,当∥平面时,( ) A、 B、 C、 D、5. 已知是两个不同的平面,是两条不同的直线,下列说法正确的是( )A、若上有两点到平面距离相等,则 B、若 , 则与是异面直线 C、若 , 则与没有公共点 D、若 , 则与一定相交6. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、
A、 B、 C、 D、5. 已知是两个不同的平面,是两条不同的直线,下列说法正确的是( )A、若上有两点到平面距离相等,则 B、若 , 则与是异面直线 C、若 , 则与没有公共点 D、若 , 则与一定相交6. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、 B、
B、 C、
C、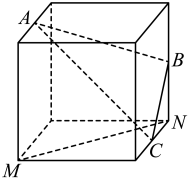 D、
D、 7. 如图所示,在棱长为1的正方体中,点分别是棱的中点,是侧面内一点,若平面 , 则线段长度的取值范围是( )
7. 如图所示,在棱长为1的正方体中,点分别是棱的中点,是侧面内一点,若平面 , 则线段长度的取值范围是( ) A、 B、 C、 D、8. 如图,该组合体由一个正四棱柱和一个正四棱锥组合而成,已知 , , , 则( )
A、 B、 C、 D、8. 如图,该组合体由一个正四棱柱和一个正四棱锥组合而成,已知 , , , 则( ) A、平面 B、平面 C、平面 D、平面
A、平面 B、平面 C、平面 D、平面二、多项选择题
-
9. 如图,在长方体中, , 点P为线段上的动点,则下列结论正确的是( )
 A、当时, , P,D三点共线 B、当时, C、当时,平面 D、当时,平面10. 已知一个正八面体如图所示, , 则( )
A、当时, , P,D三点共线 B、当时, C、当时,平面 D、当时,平面10. 已知一个正八面体如图所示, , 则( ) A、平面 B、点到平面的距离为1 C、异面直线与所成的角为 D、四棱锥外接球的表面积为11. 如图,在正方体中, , 均为所在棱的中点,是正方体表面上的动点,则下列说法正确的是( )
A、平面 B、点到平面的距离为1 C、异面直线与所成的角为 D、四棱锥外接球的表面积为11. 如图,在正方体中, , 均为所在棱的中点,是正方体表面上的动点,则下列说法正确的是( ) A、平面 B、三棱锥的体积为 C、过三点的平面截正方体所得截面的面积为 D、若 , 则点的轨迹长度为
A、平面 B、三棱锥的体积为 C、过三点的平面截正方体所得截面的面积为 D、若 , 则点的轨迹长度为三、填空题
-
12. 三棱锥的所有棱长均为2,E,F分别为线段BC与AD的中点,M,N分别为线段AE与CF上的动点,若平面ABD,则线段MN长度的最小值为 .13. 如图,在棱长为3的正方体中,在线段上,且是侧面上一点,且平面 , 则线段的最大值为.
 14. 三棱锥中,和均为边长为2的等边三角形,分别在棱上,且平面平面 , 若 , 则平面与三棱锥的交线围成的面积最大值为 .15. 如图,长方体木块中, , , E,F,G分别是线段 , , DC的中点,平面上存在点P,满足平面EFG,则点D与满足题意的点P构成的平面截长方体所得截面的面积为 .
14. 三棱锥中,和均为边长为2的等边三角形,分别在棱上,且平面平面 , 若 , 则平面与三棱锥的交线围成的面积最大值为 .15. 如图,长方体木块中, , , E,F,G分别是线段 , , DC的中点,平面上存在点P,满足平面EFG,则点D与满足题意的点P构成的平面截长方体所得截面的面积为 .
四、解答题
-
16. 如图所示,四棱锥的底面是矩形,底面 , , , , .
 (1)、证明:平面;(2)、求直线与平面所成角的余弦值.17. 如图,在四棱锥中,底面为正方形、平面分别为棱的中点
(1)、证明:平面;(2)、求直线与平面所成角的余弦值.17. 如图,在四棱锥中,底面为正方形、平面分别为棱的中点 (1)、证明:平面;(2)、若 , 求直线与平面所成角的正弦值
(1)、证明:平面;(2)、若 , 求直线与平面所成角的正弦值

