2025高考一轮复习（人教A版）第二十一讲空间点、直线、平面之间的位置关系

试卷更新日期：2024-12-22 类型：一轮复习

进入出卷网下载

一、选择题

1. 设 $a ， b$ 为两条直线， $α ， β$ 为两个平面，下列四个命题中，正确的命题是（　　）

A、若 $a ， b$ 与 $α$ 所成的角相等，则 $a ∥ b$ B、若 $a ∥ α ， b ∥ β$ ， $α ∥ β$ ，则 $a ∥ b$ C、若 $a \subset α ， b \subset β ， a ∥ b$ ，则 $α ∥ β$ D、若 $a ⊥ α ， b ⊥ β$ ， $α ⊥ β$ ，则 $a ⊥ b$

查看试题解析
2. 设正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为1，高为2，平面 $α$ 经过顶点 $A$ ，且与棱 $A B, A D, A A_{1}$ 所在直线所成的角都相等，则满足条件的平面 $α$ 共有（）个．

A、1 B、2 C、3 D、4

查看试题解析
3. 已知平面 $α ⊥$ 平面 $β$ ，直线 $l ⊄ α$ ，则“ $l ⊥ β$ ”是“ $l / / α$ ”的( )

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 下列命题一定正确的是（）

A、一条直线和一个点确定一个平面 B、如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行 C、垂直于同一条直线的两条直线互相平行 D、若直线 $l$ 与平面 $α$ 平行，则直线 $l$ 与平面 $α$ 内任意一条直线都没有公共点

查看试题解析
5. $l$ 为直线， $α$ 为平面，则下列条件能作为 $l / / α$ 的充要条件的是( )

A、 $l$ 平行平面 $α$ 内的无数条直线 B、 $l$ 平行于平面 $α$ 的法向量 C、 $l$ 垂直于平面 $α$ 的法向量 D、 $l$ 与平面 $α$ 没有公共点

查看试题解析
6. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E, F, G, H$ 分别是棱 $A A_{1}, A B, B C, C_{1} D_{1}$ 的中点，下列结论正确的是（）.

A、 $E F$ $∥$ $G D_{1}$ B、 $D_{1} E ⊥ F G$ C、 $F G ⊥$ 平面 $B B_{1} D_{1} D$ D、平面 $D_{1} E F$ $∥$ 平面 $G H C_{1}$

查看试题解析
7. 如图，点 $A$ ， $B$ ， $C$ ， $M$ ， $N$ 为正方体的顶点或所在棱的中点，则下列各图中，不满足直线 $M N / /$ 平面 $A B C$ 的是( )

A、 B、
C、 D、

查看试题解析
8. 如图是一个正方体的平面展开图，则在正方体中 $A B$ 与 $C D$ 的位置关系是( )

A、平行
B、相交
C、异面
D、不平行

查看试题解析
9. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，动点 $E$ 在线段 $A_{1} C_{1}$ 上， $F$ ， $M$ 分别是 $A D$ ， $C D$ 的中点，则下列结论中错误的是 $($ $)$

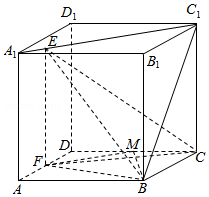A、 $F M / / A_{1} C_{1}$ B、当E为 $A_{1} C_{1}$ 中点时，BE⊥FM C、三棱锥 $B - C E F$ 的体积为定值 D、存在点 $E$ ，使得平面 $B E F / /$ 平面 $C C_{1} D_{1} D$

查看试题解析

二、多项选择题

10. 已知直线 $l, m, n$ 是三条不同的直线， $α, β$ 为两个不同的平面，则（）

A、若 $l$ $//$ $m, l$ $//$ $n, m \subset α, n \subset α$ ，则 $l$ $//$ $α$ B、若 $l ⊥ α, l$ $//$ $m, m ⊄ β, α ⊥ β$ ，则 $m$ $//$ $β$ C、若 $l ⊥ m, l ⊥ n, m \subset α, n \subset α$ ，则 $l ⊥ α$ D、若 $l$ $//$ $α, l \subset β, α \cap β = m, m$ $//$ $n$ ，则 $l$ $//$ $n$

查看试题解析
11. 在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A A_{1}$ ，点 $P$ 满足 $\vec{B P} = λ \vec{B C} + μ \vec{B B_{1}} (λ \in [0, 1], μ \in[0, 1])$ ，则下列说法正确的是（）

A、当 $λ = 1$ 时，点 $P$ 在棱 $B B_{1}$ 上 B、当 $μ = 1$ 时，点 $P$ 到平面 $A B C$ 的距离为定值 C、当 $λ = \frac{1}{2}$ 时，点 $P$ 在以 $B C, B_{1} C_{1}$ 的中点为端点的线段上 D、当 $λ = 1, μ = \frac{1}{2}$ 时， $A_{1} B ⊥$ 平面 $A B_{1} P$

查看试题解析
12. 如图，在底面为等边三角形的直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C = 2$ ， $B B_{1} = \sqrt{2}$ ， $D$ ， $E$ 分别为棱 $B C$ ， $B B_{1}$ 的中点，则（）

A、 $A_{1} B ∥$ 平面 $A D C_{1}$ B、 $A D ⊥ C_{1} D$ C、异面直线 $A C$ 与 $D E$ 所成角的余弦值为 $\frac{\sqrt{10}}{5}$ D、平面 $A D C_{1}$ 与平面 $A B C$ 的夹角的正切值为 $\sqrt{2}$

查看试题解析
13. 如图，在棱长均为1的平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $B B_{1} ⊥$ 平面 $A B C D, ∠ A B C = 60^{\circ}$ ， $P, Q$ 分别是线段 $A C$ 和线段 $A_{1} B$ 上的动点，且满足 $\vec{B Q} = λ \vec{B A_{1}}, \vec{C P} = (1 - λ) \vec{C A}$ ，则下列说法正确的是（）

A、当 $λ = \frac{1}{2}$ 时， $P Q$ $/ /$ $A_{1} D$ B、当 $λ = \frac{1}{2}$ 时，若 $\vec{P Q} = x \vec{A B} + y \vec{A D} + z \vec{A A_{1}} (x, y, z \in R)$ ，则 $x + y + z = 0$ C、当 $λ = \frac{1}{3}$ 时，直线 $P Q$ 与直线 $C C_{1}$ 所成角的大小为 $\frac{π}{6}$ D、当 $λ \in (0, 1)$ 时，三棱锥 $Q - B C P$ 的体积的最大值为 $\frac{\sqrt{3}}{48}$

查看试题解析

三、填空题

14. 设α、β为互不重合的平面，m，n是互不重合的直线，给出下列四个命题：
①若m∥n，则m∥α；
②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；
③若α∥β，m⊂α，n⊂β，则m∥n；
④若α⊥β，α∩β＝m，n⊂α，m⊥n，则n⊥β；
其中正确命题的序号为．

查看试题解析
15. 设 $α ， β$ 是两个不同的平面， $m$ 是直线且 $m \subset α$ .“ $m / / β$ ”是“ $α / / β$ ”的条件.（填“充分不必要”､“必要不充分”､“充要”､“不充分不必要”）

查看试题解析
16. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点F是棱 $A A_{1}$ 上的一个动点，平面 $B F D_{1}$ 交棱 $C C_{1}$ 于点E，则下列正确说法的序号是.
①存在点F使得 $A_{1} C_{1} ∥$ 平面 $B E D_{1} F$ ；
②存在点F使得 $B_{1} D ∥$ 平面 $B E D_{1} F$ ；
③对于任意的点F，都有 $E F ⊥ B D$ ；
④对于任意的点F三棱锥 $E - F D D_{1}$ 的体积均不变.

查看试题解析

四、解答题

17. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} ⊥$ 平面 $A B C$ ， $A B ⊥ A C$ ， $A B = A C = A A_{1} = 1$ ， $M$ 为线段 $A_{1} C_{1}$ 上一点.

(1)、求证： $B M ⊥ A B_{1}$ ；

(2)、若直线 $A B_{1}$ 与平面 $B C M$ 所成角为 $\frac{π}{4}$ ，求点 $A_{1}$ 到平面 $B C M$ 的距离.

查看试题解析
18. 如图，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $B C = B B_{1}$ ， $B C_{1} \cap B_{1} C = O$ ， $A O ⊥$ 平面 $B B_{1} C_{1} C$ .

(1)、求证： $A B ⊥ B_{1} C$ ；

(2)、若 $∠ B_{1} B C = 60 °$ ，直线 $A B$ 与平面 $B B_{1} C_{1} C$ 所成的角为 $30 °$ ，求二面角 $A_{1} - B_{1} C_{1} - A$ 的余弦值.

查看试题解析
19. 如图，已知四边形 $A B C D$ 为菱形，四边形 $A C E F$ 为平行四边形，且 $A B = 6$ ， $∠ B A D = ∠ B A F = ∠ D A F = 60 °$ .

(1)、证明：直线 $B D ⊥$ 平面 $A C E F$ ；

(2)、设平面 $B E F \cap$ 平面 $A B C D = l$ ，且二面角 $E - l - D$ 的平面角为 $θ$ ， $\tan θ = \frac{2 \sqrt{6}}{3}$ ，设 $G$ 为线段 $A F$ 的中点，求 $D G$ 与平面 $A B C D$ 所成角的正弦值.

查看试题解析
20. 如左图所示，在直角梯形 $A B C D$ 中， $B C ∥ A D$ ， $A D ⊥ C D$ ， $B C = 2$ ， $A D = 3$ ， $C D = \sqrt{3}$ ，边 $A D$ 上一点E满足 $D E = 1$ .现将 $△ A B E$ 沿 $B E$ 折起到 $△ A_{1} B E$ 的位置，使平面 $A_{1} B E ⊥$ 平面 $B C D E$ ，如右图所示.

(1)、求证： $A_{1} C ⊥ B E$ ；

(2)、求 $A_{1} D$ 与面 $B C D E$ 所成的角；

(3)、求平面 $A_{1} B E$ 与平面 $A_{1} C D$ 所成锐二面角的余弦值.

查看试题解析