【提升版】北师大版数学八年级上册第七章平行线的证明 章节测试卷
试卷更新日期:2024-12-16 类型:单元试卷
一、选择题(每题3分,共24分)
-
1. 有下列四种说法:
(1)两条直线的位置关系有相交和平行两种
(2)过一点能作一条直线与已知直线垂直
(3)过直线外一点有且只有一条直线与这条直线平行
其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个2. 如图,点A在点B的北偏东方向,点C在点B的北偏东方向,A点在C处的北偏西方向,则的度数是( ) A、 B、 C、 D、3. 如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A的度数等于( )
A、 B、 C、 D、3. 如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A的度数等于( ) A、70° B、60° C、50° D、40°4. 如图,将一副三角板平放在一平面上(点D在上),则的度数为( )
A、70° B、60° C、50° D、40°4. 如图,将一副三角板平放在一平面上(点D在上),则的度数为( )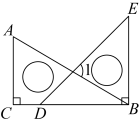 A、 B、 C、 D、5. 某城市几条道路的位置如图所示,道路与道路平行,道路与道路的夹角为 . 城市规划部门想修一条新道路 , 要求 , 则的大小为( )
A、 B、 C、 D、5. 某城市几条道路的位置如图所示,道路与道路平行,道路与道路的夹角为 . 城市规划部门想修一条新道路 , 要求 , 则的大小为( ) A、 B、 C、 D、6. 下列命题中,属于真命题的是( )A、一个角的补角一定大于这个角 B、垂直于同一条直线的两条直线平行 C、边长分别为7cm、24cm、25cm的三角形是直角三角形 D、一个角的两边与另一个角的两边分别平行,则这两个角相等7. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( )
A、 B、 C、 D、6. 下列命题中,属于真命题的是( )A、一个角的补角一定大于这个角 B、垂直于同一条直线的两条直线平行 C、边长分别为7cm、24cm、25cm的三角形是直角三角形 D、一个角的两边与另一个角的两边分别平行,则这两个角相等7. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( ) A、 B、 C、 D、8. 如图,在 中, ,将 沿直线 翻折,点 落在点 的位置,则 的度数是( )
A、 B、 C、 D、8. 如图,在 中, ,将 沿直线 翻折,点 落在点 的位置,则 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
9. 如图所示,的一边为平面镜, , 一束光线(与水平线平行)从点C射入经平面镜上的点D后,反射光线落在上的点E处,则的度数是 .
 10. 如图, 是 中 的平分线, 是 的外角的平分线,如果 ,则 .
10. 如图, 是 中 的平分线, 是 的外角的平分线,如果 ,则 .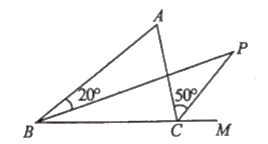 11. 若等腰三角形一腰上的高与另一腰的夹角为 , 则这个等腰三角形的底角度数是 .12. 在如图的五角星中,°
11. 若等腰三角形一腰上的高与另一腰的夹角为 , 则这个等腰三角形的底角度数是 .12. 在如图的五角星中,° 13. 命题“同位角相等,两直线平行”中,条件是 结论是
13. 命题“同位角相等,两直线平行”中,条件是 结论是三、解答题(共7题,共61分)
-
14. 如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC∶∠B∶∠C=4∶3∶2,求∠DAE的度数.
 15. 如图,是的外角, .
15. 如图,是的外角, . (1)、请你用尺规作图的方法作的角平分线;(不写作法,保留作图痕迹)(2)、判断与的位置关系,并说明理由.16. 如图,在中,和的平分线相交于点 .
(1)、请你用尺规作图的方法作的角平分线;(不写作法,保留作图痕迹)(2)、判断与的位置关系,并说明理由.16. 如图,在中,和的平分线相交于点 . (1)、若 , 求的度数.(2)、当为多少度时,?17. 综合与实践
(1)、若 , 求的度数.(2)、当为多少度时,?17. 综合与实践综合与实践课上,老师让同学们以“三角形的折叠”为主题开展数学活动.
 (1)、 操作判断
(1)、 操作判断操作一:折叠三角形纸片,使与边在一条直线上,得到折痕;
操作二:折叠三角形纸片,得到折痕 , 使 , , 三点在一条直线上.
完成以上操作后把纸片展平,如图1,判断和的大小关系是 , 直线 , 的位置关系是 .
(2)、深入探究操作三:折叠三角形纸片,使点落在折痕上,得到折痕 , 把纸片展平.
根据以上操作,如图2,判断和是否相等,并说明理由.
(3)、 结论应用如图1,已知 , , 请直接写出的度数.
18. 已知:在中,平分 , 平分 . (1)、如图1,若 , , 求的度数.(2)、如图2,连接 , 作 , , , 求的面积.19. 如图,在四边形ABCD中,AD∥BC,∠DAB的平分线交BC的延长线于点E,BG⊥AE,垂足为点F,交CD于点G.
(1)、如图1,若 , , 求的度数.(2)、如图2,连接 , 作 , , , 求的面积.19. 如图,在四边形ABCD中,AD∥BC,∠DAB的平分线交BC的延长线于点E,BG⊥AE,垂足为点F,交CD于点G. (1)、求证:BG平分∠ABE;(2)、若∠DCB=100°,∠DAB=60°,求∠BGC的度数.20. 阅读下列材料并解答问题:
(1)、求证:BG平分∠ABE;(2)、若∠DCB=100°,∠DAB=60°,求∠BGC的度数.20. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”. 例如:一个三角形三个内角的度数分别是 , 这个三角形就是一个“3倍角三角形”. 反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
 (1)、如图①,已知 , 在射线上取一点 , 过点作交于点 , 判断是不是“3倍角三角形”,为什么?(2)、在(1)的条件下,以为端点画射线 , 交线段于点(点不与点、点重合),若是“3倍角三角形”,求的度数;(3)、如图②,点在的边上,连接 , 作的平分线交于点 , 在上取一点 , 使得 , 若是“3倍角三角形”,求的度数.
(1)、如图①,已知 , 在射线上取一点 , 过点作交于点 , 判断是不是“3倍角三角形”,为什么?(2)、在(1)的条件下,以为端点画射线 , 交线段于点(点不与点、点重合),若是“3倍角三角形”,求的度数;(3)、如图②,点在的边上,连接 , 作的平分线交于点 , 在上取一点 , 使得 , 若是“3倍角三角形”,求的度数.