【提升版】北师大版数学八年级上册7.5三角形内角和定理同步练习

试卷更新日期：2024-12-12 类型：同步测试

进入出卷网下载

一、选择题

1. $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别是 $a$ 、 $b$ 、 $c$ ，下列条件不能判定 $△ A B C$ 是直角三角形的（　　）

A、 $∠ C - ∠ B = ∠ A$ B、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$ C、 $(c + a) (c - a) = b^{2}$ D、 $a : b : c = 7 : 24 : 25$

查看试题解析
2. 如图，两面镜子 $A B, B C$ 的夹角为 $α$ ，当光线经过镜子反射时，入射角等于反射角，即 $∠ 1 = ∠ 2$ ， $∠ 3= ∠ 4$ ．若 $∠ α = 70 °$ ， $∠ 1 = 35 °$ ，则 $∠ 4$ 的度数为（）

A、 $70 °$ B、 $75 °$ C、 $80 °$ D、 $85 °$

查看试题解析
3. 如图，直线 $A B / / C D ， G E ⊥ E F$ 于点 $E$ .若 $∠ E F D = 3 2^{°}$ ，则 $∠ B G E$ 的度数是（）

A、 $6 2^{°}$ B、 $5 8^{°}$ C、 $5 2^{°}$ D、 $4 8^{°}$

查看试题解析
4. 如图，将一张三角形纸片 $A B C$ 的一角折叠，使点 $A$ 落在 $Δ A B C$ 处的 $A^{'}$ 处，折痕为 $D E$ .如果 $∠ A = α$ ， $∠ C E A^{'} = β$ ， $∠ B D A^{'} = γ$ ，那么下列式子中正确的是（）

A、 $γ = 2 α + β$ B、 $γ = α + 2 β$ C、 $γ = α + β$ D、 $γ = 180^{\circ} - α - β$

查看试题解析
5. 等腰三角形的一个底角等于 $55 °$ ，则它的顶角等于（）

A、 $45 °$ B、 $55 °$ C、 $70 °$ D、 $80 °$

查看试题解析
6. 满足下列条件的三角形中，不是直角三角形的是（）

A、三内角的度数之比为1：2：3 B、三内角的度数之比为3：4：5 C、三边长之比为3：4：5 D、三边长的平方之比为1：2：3

查看试题解析
7. 如图，在△ABC中，以点B为圆心，AB为半径画弧交BC于点D，以点C为圆心，AC为半径画弧交BC于点E，连接AE，AD．设∠EAD＝α，∠ACB＝β，则∠B的度数为（）

A、α﹣ $\frac{β}{2}$ B、2α﹣β C、α+ $\frac{β}{2}$ D、3α﹣β

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A = 40 °$ ， $∠ C = 70 °$ ， $A B$ 的垂直平分线分别交 $A B ， A C$ 于点D，E，连接 $B E$ ，则 $∠ E B C$ 的大小为（　　）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $80 °$

查看试题解析

二、填空题

9. 在 $△ A B C$ 中， $A B = A C$ ， $B D$ 是 $A C$ 边上的高， $∠ A B D = 50 °$ ，则 $∠ C$ 的度数为．

查看试题解析
10. 等边三角形的每个内角为度。

查看试题解析
11. 一副三角板如图叠放在一起，则图中α的度数为．

查看试题解析
12. 一个零件的形状如图所示，按规定 $∠ A$ 应等于 $90 °$ ．已知 $∠ B, ∠ C$ ，分别是 $34 °$ 和 $18 °$ ，李伯伯量得 $∠ B D C = 146 °$ ，则这个零件是否合格？．（填“合格”或“不合格）

查看试题解析
13. 如图，将 $△ A B C$ 沿经过点 $A$ 的直线 $A D$ 折叠，使边 $A C$ 所在的直线与边 $A B$ 所在的直线重合，点 $C$ 落在边 $A B$ 上的 $E$ 处，若 $∠ B = 45 °$ ， $∠ B D E = 20 °$ ，则 $∠ C A D =$ ．

查看试题解析

三、解答题

14. 如图， $△ A B C$ 中，已知 $C D$ 为 $∠ A C B$ 的平分线， $A M ⊥ C D$ 于 $M$ ， $∠ B = 45 °$ ， $∠ B A M = 8 °$ ，求 $∠ A C B$ 的度数．

查看试题解析
15. 如图， $P$ 是 $△ A B C$ 内一点， $∠ C = 70 °$ .

(1)、若 $∠ P A C = 20 °$ ， $∠ P B C = 40 °$ ，求 $∠ A P B$ 的度数.

(2)、若 $P A$ ， $P B$ 分别为 $∠ C A B$ ， $∠ C B A$ 的平分线，求 $∠ A P B$ 的度数.

查看试题解析
16. 如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．
小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．

(1)、按小明的思路，求∠APC的度数；
（问题迁移）

(2)、如图2，AB∥CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
（问题应用）

(3)、在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系（并画出相应的图形）．

查看试题解析
17. 【问题呈现】
如图①，已知线段 $A C$ ， $B D$ 相交于点 $O$ ，连结 $A B$ ， $C D$ ，我们把形如这样的图形称为“ $8$ 字型”．

(1)、证明： $∠ A + ∠ B = ∠ C + ∠ D$ ．

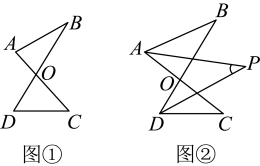(2)、【问题探究】
继续探究，如图②， $A P$ 、 $D P$ 分别平分 $∠ B A O$ 、 $∠ C D O$ ， $A P$ 、 $D P$ 交于点 $P$ ，求 $∠ P$ 与 $∠ B$ 、 $∠ C$ 之间的数量关系．为了研究这一问题，尝试代入 $∠ B$ 、 $∠ C$ 的值求 $∠ P$ 的值，得到下面几组对应值：
表中 $a =$ ，猜想得到 $∠ P$ 与 $∠ B$ 、 $∠ C$ 的数量关系为；

(3)、证明（ $2$ ）中猜想得到的 $∠ P$ 与 $∠ B$ 、 $∠ C$ 的数量关系；
$∠ B$ （单位：度）
$20$
$35$
$40$
$∠ C$ （单位：度）
$30$
$45$
$20$
$∠ P$ （单位：度）
$25$
$40$
$a$

查看试题解析
18. 如图，在 $Δ A B C$ 中，点 $D$ 为 $A C$ 边上一点，连结 $B D$ 并延长到点 $E$ ，过点 $E$ 作 $E F / / B C$ 交 $A C$ 于点 $F$ ，交 $A B$ 于点 $G$ ．

(1)、若 $B D = D E$ ，求证： $C D = D F$ ；

(2)、若 $B G = G E$ ， $∠ A C B = 70 °$ ， $∠ E = 25 °$ ，求 $∠ A$ 的度数．

查看试题解析
19. 如图，在△ABC中，AE，CD分别是∠BAC， ∠ACB的平分线，且AE，CD相交于点F．

(1)、若∠BAC=80°，∠ACB=40°，求∠AFC的度数；

(2)、若∠B=80°，求∠AFC的度数；

(3)、若∠B=x°，用含x的代数式表示∠AFC的度数．

查看试题解析
20. 如图

(1)、在图1中，请直接写出 $∠ A$ 、 $∠ B$ 、 $∠ C$ 、 $∠ D$ 之间的数量关系：；

(2)、仔细观察，在图2中“8字形”的个数个；

(3)、如果图2中， $∠ D = 40 °$ ， $∠ B = 36 °$ ， $A P$ 与 $C P$ 分别是 $∠ D A B$ 和 $∠ D C B$ 的角平分线，试求 $∠ P$ 的度数；

(4)、如果图2中 $∠ D$ 和 $∠ B$ 为任意角，其他条件不变，试问 $∠ P$ 与 $∠ D$ ， $∠ B$ 之间存在着怎样的数量关系（直接写出结论即可）．

查看试题解析

$∠ B$ （单位：度）	$20$	$35$	$40$
$∠ C$ （单位：度）	$30$	$45$	$20$
$∠ P$ （单位：度）	$25$	$40$	$a$

【提升版】北师大版数学八年级上册7.5三角形内角和定理 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学八年级上册7.5三角形内角和定理同步练习