8字相似模型—浙教版数学九（上）知识点训练

试卷更新日期：2024-12-07 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，线段 $A B$ ， $C D$ 相交于点 $O$ ， $A C ∥ B D$ ，若 $O A = 6$ ， $O C = 3$ ， $O D = 2$ ，则 $O B$ 的长是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于

A、 $\frac{20}{3}$ B、 $\frac{15}{4}$ C、 $\frac{16}{3}$ D、 $\frac{17}{4}$

查看试题解析
3.
如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点O，设△OCD的面积为m，△OEB的面积为 $\sqrt{5}$ ，则下列结论中正确的是（　　）

A、m=5 B、m=4 $\sqrt{5}$ C、m=3 $\sqrt{5}$ D、m=10

查看试题解析
4. 如图，△ABC的中线BD，CE交于点G，且△ABC的面积为12，则（）

A、∠ADE＝∠AEC B、BG＝2DG C、CD²＝DG∙DB D、△DEG的面积为1.5

查看试题解析
5. 如图，正方形 $C E F G$ 的顶点G在正方形 $A B C D$ 的边 $C D$ 上， $A F$ 与 $D C$ 交于点H ，若 $A B = 6$ ， $C E = 2$ ，则 $D H$ 的长为（）

A、2 B、3 C、 $\frac{5}{2}$ D、 $\frac{8}{3}$

查看试题解析
6. 如图，点D，E，F分别在 $△ A B C$ 的边上， $\frac{A D}{B D} = \frac{1}{3}$ ， $D E ∥ B C$ ， $E F ∥ A B$ ， M是 $D F$ 的中点，连结 $C M$ 并延长交 $A B$ 于点N，则 $\frac{M N}{C M}$ 的值是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{9}$ C、 $\frac{1}{6}$ D、 $\frac{1}{7}$

查看试题解析
7. 凸透镜成像的原理如图所示， $A D ∥ l ∥ B C$ .若物体到焦点的距离与焦点到凸透镜中心线 $D B$ 的距离之比为 $5 ： 4$ ，则物体被缩小到原来的（）

A、 $\frac{4}{5}$ B、 $\frac{2}{5}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
8. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 是 $B C$ 上的一点，且 $B D : C D = 1 : 2$ ， $E$ 是 $A B$ 的中点，连结 $A D$ ， $C E$ 交于点 $F$ ．若 $A C = C D = 2$ 时，则阴影部分 $△ A C F$ 的面积为（）

A、 $\frac{4}{5}$ B、 $\frac{6}{5}$ C、 $\frac{4}{3}$ D、 $\frac{5}{3}$

查看试题解析

二、填空题

9. 如图， $A B$ 与 $C D$ 交于点 $O$ ，且 $A C ∥ B D$ ．若 $\frac{O A + O C + A C}{O B + O D + B D} = \frac{1}{2}$ ，则 $\frac{A C}{B D} =$ ．

查看试题解析
10. 如图，B ， F ， C三点共线，AC与BD交于点E ， $E F ∥ A B ∥ D C$ ，若BF：CF＝5：7，则 $\frac{S_{△ A B E}}{S_{△ C D E}}$ 的值为．

查看试题解析
11. 如图所示，在△ABC中，E、D分别是AC、AB的中点，连结BE、CD相交于点G ，若CD⊥BE ， BE＝12，CD＝9，则四边形ADGE的面积为．

查看试题解析
12. 如图， $D$ 、 $E$ 分别是 $△ A B C$ 的边 $A B$ 、 $B C$ 上的点， $D E / / A C$ ，若 $S_{△ D O E}$ ： $S_{△ C O A} = 1$ ： $25$ ，则 $S_{△ B D E}$ ： $S_{△ C D E} =$ ．

查看试题解析

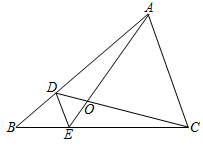
三、解答题

13. 如图，
AD与BC交于点O，EF过点O，交AB于点E，交CD于点F ，BO=1，CO= 3，AO= $\frac{3}{2}$ ， DO= $\frac{9}{2}$

(1)、求证：∠A=∠D.

(2)、若AE= BE，求证：CF= DF.

查看试题解析
14. 如图，四边形ABCD中，AC平分∠DAB ， AC²＝AB•AD ， ∠ADC＝90°，E为AB的中点．

(1)、求证：△ADC∽△ACB；

(2)、若AD＝4，AB＝6，求 $\frac{A C}{A F}$ 的值．

查看试题解析
15. 如图，点D、E是△ABC边AB、AC的中点，连接BE，点G是线段BE的中点，连接CG并延长，交ED的延长线于点 $F$ ，交AB于点 $H$ .

(1)、求 $\frac{F H}{C H}$ 的值；

(2)、 $F C = 18$ ，求HG的长.

查看试题解析
16. 如图，四边形 $A B C D$ 中， $A C$ 平分 $∠ D A B$ ， $∠ A D C = ∠ A C B = 90 °$ ， $E$ 为 $A B$ 的中点，连接 $C E$ ， $D E$ ．

(1)、求证： $A C^{2} = A B \cdot A D$ ；

(2)、若 $A D = 4$ ， $A B = 6$ ，求 $\frac{A F}{F C}$ 的值．

查看试题解析
17. 如图，AC是⊙O的直径，弦BD交AC于点E.

(1)、求证：△ADE∽△BCE；

(2)、如果AD²＝AE·AC，求证：CD＝CB.

查看试题解析
18. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 与直线 $l : y = k x + m$ 交于 $A (1, 1)$ ， B两点，与y轴交于 $C (0, 5)$ ，直线l与y轴交于点D ．

(1)、求抛物线的函数解析式；

(2)、设直线l与抛物线的对称轴的交点为F ，若 $\frac{A F}{F B} = \frac{3}{4}$ ，求直线l的函数解析式；

(3)、若在x轴上存在一点P ，使 $∠ A P B = 90 °$ ，且 $A P = B P$ ，求出h的值．

查看试题解析
19. 【阅读与思考】
下面是一位同学的数学学习笔记，请仔细阅读并完成相应的任务.
任务：

(1)、笔记中横线部分应填写①；
②∽ ， ∽.

(2)、如图 2，在 $△ M N H$ 中，点 $K, L$ 分别在 $M N, M H$ 边上，连接 $H K, N L$ 交于点 $F$ . 若 $M K = \frac{1}{3} M N$ ， $M L = \frac{1}{3} M H$ ，猜测 $K F$ 与 $H F$ 的数量关系，并说明理由.

(3)、如图 3，在平行四边形 $A B C D$ 中，点 $E 、 F 、 G$ 分别是 $A D 、 B C 、 C D$ 的中点， $B E ⊥ E G$ ， $A B = 3, A D = 2 \sqrt{5}$ ，求 $A F$ 长.

查看试题解析