三角形的重心—浙教版数学九(上)知识点训练
试卷更新日期:2024-12-07 类型:复习试卷
一、选择题
-
1. 如图所示,在中,点D是斜边AB的中点,点G是的重心,于点E , 若 , 那么GE的长为( )
 A、1 B、2 C、3 D、2. 如图,已知AD为△ABC中BC边上的中线,过重心G作GE∥AC,交BC于点E,DE=2,则BC的长为( )
A、1 B、2 C、3 D、2. 如图,已知AD为△ABC中BC边上的中线,过重心G作GE∥AC,交BC于点E,DE=2,则BC的长为( )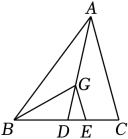 A、12 B、8 C、6 D、43. 如图,在Rt中, , 点为斜边上的中点,点为的重心,那么( )
A、12 B、8 C、6 D、43. 如图,在Rt中, , 点为斜边上的中点,点为的重心,那么( ) A、 B、 C、 D、4. 如图,AE,CF分别是等腰Rt△ABC中CB、AB边上的中线,相交于点G,若斜边AB的长为6,则AG长为( )
A、 B、 C、 D、4. 如图,AE,CF分别是等腰Rt△ABC中CB、AB边上的中线,相交于点G,若斜边AB的长为6,则AG长为( )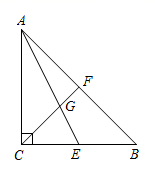 A、3 B、3 C、 D、5. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( )
A、3 B、3 C、 D、5. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( ) A、1 B、 C、 D、26. 如图,点P是△ABC的重心,若△ABC的面积为12,则△BPC的面积为( )
A、1 B、 C、 D、26. 如图,点P是△ABC的重心,若△ABC的面积为12,则△BPC的面积为( )
 A、3 B、4 C、5 D、67. 如图, 是 的角平分线, 交 于点E,若 的重心G在 上,则 的值是( )
A、3 B、4 C、5 D、67. 如图, 是 的角平分线, 交 于点E,若 的重心G在 上,则 的值是( ) A、 B、 C、 D、8. 如图,点G是的重心,过点G作分别交AB,AC于点M,N,过点N作交BC于点D,则四边形BDNM与的面积之比是( )
A、 B、 C、 D、8. 如图,点G是的重心,过点G作分别交AB,AC于点M,N,过点N作交BC于点D,则四边形BDNM与的面积之比是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 三角形三边长为5,5,6,则这个三角形的外心和重心的距离为.10. 如图,AD、CE是△ABC的中线,若△CDG的面积是1,则△ABC的面积为 .
 11. 已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为.12. 如图,在△ABC中,中线AD,BE相交于点O.若S△BOD=5,则S△AOB= , S△ABC=.
11. 已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为.12. 如图,在△ABC中,中线AD,BE相交于点O.若S△BOD=5,则S△AOB= , S△ABC=.
三、解答题
-
13. 如图在的网格中,的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
 (1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.14. 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC于点D,E,F.
(1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.14. 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC于点D,E,F. (1)、求的值.(2)、若AB=12cm,求PD+PE+PF的值.15. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、求的值.(2)、若AB=12cm,求PD+PE+PF的值.15. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.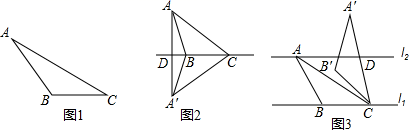 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,DC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形.(填“是”或“否”)
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连接AA'交直线BC于点D.若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2,“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C,A′C所在直线交l2于点D,直接写出CD的值.