相似三角形的判定—浙教版数学九(上)知识点训练
试卷更新日期:2024-12-07 类型:复习试卷
一、对应角相等的两个三角形相似
-
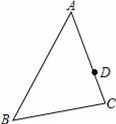
1. 如图,△ABC的中线BD,CE交于点G,且△ABC的面积为12,则( )
 A、∠ADE=∠AEC B、BG=2DG C、CD2=DG∙DB D、△DEG的面积为1.52. 如图,在中, , 是边上的高, , , 则等于( )
A、∠ADE=∠AEC B、BG=2DG C、CD2=DG∙DB D、△DEG的面积为1.52. 如图,在中, , 是边上的高, , , 则等于( ) A、 B、 C、 D、3. 如图,已知 , , , , 则 .
A、 B、 C、 D、3. 如图,已知 , , , , 则 . 4. 如图,在△ABC中,D是AC上一点,已知 .
4. 如图,在△ABC中,D是AC上一点,已知 . (1)、求证:∠ABD=∠C;(2)、已知∠A=20°,∠C=40°,求∠CBD的度数.
(1)、求证:∠ABD=∠C;(2)、已知∠A=20°,∠C=40°,求∠CBD的度数.二、三边对应成比例的两个三角形相似
-
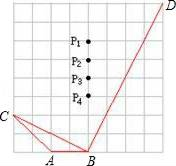
5. △ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )A、AB=c,AC=b,BC=a,DE= , EF= , DF= B、AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1 C、AB=3,AC=4,BC=6,DE=12,EF=8,DF=6 D、AB= , AC= , BC= , DE= , EF=3,DF=36. 如图,在正方形网格上,若使 , 则点P应在 .
 7. 如图,D、E分别是△ABC的边AB、AC上的点,AB=9,BD=7,AC=6,CE=3,求证:△ADE∽△ACB.
7. 如图,D、E分别是△ABC的边AB、AC上的点,AB=9,BD=7,AC=6,CE=3,求证:△ADE∽△ACB.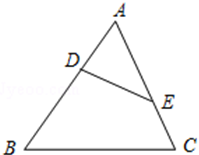
三、两边对应成比例,且夹角相等的两个三角形相似
-
8. 下列各组条件中,能判定△ABC与△A'B'C'相似的是( )A、 B、 , 且∠A=∠C' C、 , 且∠B=∠A' D、 , 且∠B=∠B'9. 如图,在中, , D是边上一点, . 求证 .
 10. 如图,△ABC的顶点均为网格中的格点.
10. 如图,△ABC的顶点均为网格中的格点. (1)、选择合适的格点(包括边界)为点D和点E,请画出一个△ADE,使△ADE∽△ABC(相似比不为1).(2)、证明:△ADE∽△ABC.
(1)、选择合适的格点(包括边界)为点D和点E,请画出一个△ADE,使△ADE∽△ABC(相似比不为1).(2)、证明:△ADE∽△ABC.四、相似三角形的判定方法综合应用
-
11. 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=3,按图中虚线剪下的三角形与△ABC不相似的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
12. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 13. 如图所示,给出下列条件:
13. 如图所示,给出下列条件: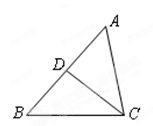
①;
②;
③;
④ .
其中单独能够判定的有( )
A、①②③④ B、①②③ C、①② D、①②④14. 如图,A,B均在方格纸的格点上.在方格纸内另取格点C,D,连结CD,交线段AB于点P.若要使点P把线段AB分成1:2的两条线段,则( ) A、只有方法1对 B、只有方法2对 C、方法1,2都对 D、方法1,2都错15. 如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件: , 使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!)
A、只有方法1对 B、只有方法2对 C、方法1,2都对 D、方法1,2都错15. 如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件: , 使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!) 16. 如图,在△ABC中,点D为边AC上的一点,选择下列条件:①∠2=∠A;②∠1=∠CBA;③;④中的一个,不能得出△ABC和△BCD相似的是:(填序号).
16. 如图,在△ABC中,点D为边AC上的一点,选择下列条件:①∠2=∠A;②∠1=∠CBA;③;④中的一个,不能得出△ABC和△BCD相似的是:(填序号).