立方和、立方差、杨辉三角—人教版数学八（上）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、立方和

1. 学习整式的乘法时可以发现：用两种不同的方法表示同一个图形的面积，可以得到一个等式，进而可以利用得到的等式解决问题．

(1)、如图 $(1)$ ，是由边长为 $a$ ， $b$ 的正方形和长为 $a$ 、宽为 $b$ 的长方形拼成的大正方形，由图 $(1)$ 可得等式：；

(2)、知识迁移：
$①$ 如图 $(2)$ 是用 $2$ 个小正方体和 $6$ 个小长方体拼成的一个大正方体，类比 $(1)$ ，用不同的方法表示这个大正方体的体积，则可得等式：；
$②$ 已知 $a + b = 7$ ， $a^{2} b = 50$ ， $a b^{2} = 20$ ，利用 $①$ 中所得等式，求代数式 $a^{3} + b^{3}$ 的值．

查看试题解析
2. 【知识生成】
通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．
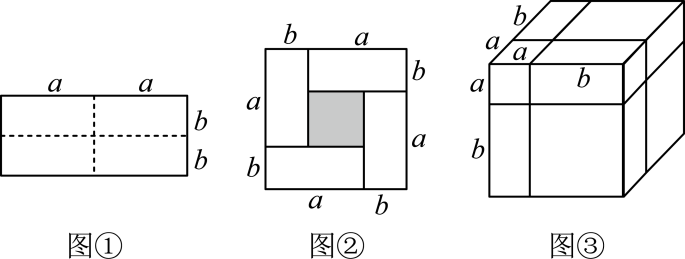
例如：如图①是个长为 $2 a$ ，宽为 $2 b$ 的长方形，沿图中虚线用剪刀将其均分成四个小长方形，然后按如图②的形状拼成一个正方形．请解答下列问题：

(1)、请用两种不同的方法表示如图②中阴影部分的面积：
方法1：；方法2：；
由此可以得出 ${(a + b)}^{2}, {(a - b)}^{2} 、 a b$ 之间的等量关系是；

(2)、【知识迁移】
类似地，用两种不同的方法计算同一几何体的体积，也可以得到一个恒等式．
如图③，请用两种不同的方法表示这个几何体的体积，并写出一个恒等式；

(3)、已知 $a + b = 3 ， a b = 1$ ，利用（2）的结论求 $\frac{a^{3} + b^{3}}{2}$ 的值．

查看试题解析
3. 学习了平方差、完全平方公式后，小聪同学对学习和运用数学公式非常感兴趣，他通过上网查阅，发现还有很多数学公式，如立方和公式：（a＋b）（a²－ab＋b²）＝a³＋b³ ，他发现，运用立方和公式可以解决很多数学问题，请你也来试试利用立方和公式解决以下问题：

(1)、【公式理解】公式中的字母可以代表任何数、字母或式子
①化简：（a－b）（a²＋ab＋b²）＝；
②计算：（99³＋1）÷（99²－99＋1）＝；

(2)、【公式运用】已知： $\frac{1}{x}$ ＋x＝5，求 $[(\frac{1}{x})^{2} + x] \div (\frac{1}{x} + 1)$ 的值：

(3)、【公式应用】如图，将两块棱长分别为a、b的实心正方体橡皮泥揉合在一起，重新捏成一个高为 $\frac{a + b}{2}$ 的实心长方体，问这个长方体有无可能是正方体，若可能，a与b应满足什么关系？若不可能，说明理由.

查看试题解析

二、立方差

4. 综合与实践：
数形结合思想是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想．我们常利用数形结合思想，借助形的几何直观性来阐明数之间某种关系，如：探索整式乘法的一些法则和公式．
探索整式乘法的一些法则和公式．

(1)、探究一：将图1的阴影部分沿虚线剪开后，拼成图2的形状，拼图前后图形的面积不变，因此可得一个多项式的分解因式．

(2)、探究二：类似地，我们可以借助一个棱长为a的大正方体进行以下探索：
在大正方体一角截去一个棱长为b（b＜a）的小正方体，如图3所示，则得到的几何体的体积为；

(3)、将图3中的几何体分割成三个长方体①、②、③，如图4，图5所示，∵BC＝a ， AB＝a﹣b ， CF＝b ， ∴长方形①的体积为ab（a﹣b）．类似地，长方体②的体积为，长方体③的体积为；（结果不需要化简）

(4)、用不同的方法表示图3中几何体的体积，可以得到的恒等式（将一个多项式因式分解）为．

(5)、问题应用：利用上面的结论，解决问题：已知a﹣b＝6，ab＝2，求a³﹣b³的值．

查看试题解析

三、杨辉三角

5. 我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉 $($ 约 $13$ 世纪 $)$ 所著的 $《$ 详解九章算术 $》$ 一书中，用如图的三角形解释二项和 $(a + b)^{n}$ 的展开式的各项系数，此三角形称为“杨辉三角”，根据“杨辉三角”计算 $(a + b)^{9}$ 的展开式中第三项的系数为（）

A、 $28$ B、 $36$ C、 $45$ D、 $56$

查看试题解析
6. 下面为杨辉三角系数表，它的作用是指导读者按规律写出形如 $(a + b)^{n}$ （其中 $n$ 为正整数）展开式的系数，请你仔细观察下面的规律，填出 $(a + b)^{6}$ 展开式中所缺的系数.则 $(a + b)^{6} = a^{6} + 6 a^{5} b + 15 a^{4} b^{2} +$ $a^{3} b^{3} + 15 a^{2} b^{4} + 6 a b^{5} + b^{6}$

查看试题解析
7.
如图，在我国南宋数学家杨辉所著的《解：九章算术》一书中，介绍了展开式的系数规律，称为“杨辉三角”.如第5行的5个数是1，4，6，4，1，恰好对应着 ${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$ 展开式中的各项系数.利用上述规律计算： $10 1^{4} - 4 \times 10 1^{3} + 6 \times 10 1^{2} - 4 \times 101 =$ .
$\begin{array}{l} {(a + b)}^{0} 1 \\ {(a + b)}^{1} 1 1 \\ {(a + b)}^{2} 1 2 1 \\ {(a + b)}^{3} 1 3 3 1 \\ {(a + b)}^{4} 1 4 6 4 1 \\ {(a + b)}^{5} 1 5 10 10 5 1 \\ \dots \dots \dots \dots \end{array}$

查看试题解析
8. 请阅读下列材料，并完成相应的任务。
杨辉，南宋杰出的数学家和数学教育家，杨辉一生留下了大量的著作，他著名的数学著作共5种21卷，即《详解九章算法》12卷，《日用算法》2卷，《乘除通变本末》3卷，《田亩比类乘除捷法》卷，《续古摘奇算法》卷。在《详解九章算法》一书中，画了一张表示二项式展开后的系数构成的三角图形，根据这个三角图形，杨辉研究了二项式定理，并根据此定理研究了两教的立方和、立方差、三数的立方和等公式，两数的立方差公式是：a³-b³=(a-b)(a²+ab+b²)，这个公式的推导过程如下：a³-b³=a³-a²b+a²b-b³=a²(a-b)+b(a²-b²)=a²(a-b)+b(a+b)(a-b)=(a-b)(a²+ab+b²)

任务：

(1)、利用上述方法推导立方和公式a³+b³=(a+b)(a²-ab+b²)从左往右推导)

(2)、已知a+b=1，ab=-1，a>b，求a²+b² ， a³-b³的值

查看试题解析

9. 阅读材料：北师大版七年级下册教材24页为大家介绍了杨辉三角．

杨辉三角如果将 $(a + b)^{n} (n$ 为非负整数）的展开式的每一项按字母 $a$ 的次数由大到小排列，就可以得到下面的等式：

$(a + b)^{0} = 1$ ，它只有一项，系数为1；

$(a + b)^{1} = a + b$ ，它有两项，系数分别为1，1；

$(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，它有三项，系数分别为1，2，1；

$(a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ ，它有四项，系数分别为1，3，3，1

将上述每个式子的各项系数排成该表.

观察该表，可以发现每一行的首末都是1，并且下一行的数比上一行多1个，中间各数都写在上一行两数的中间，且等于它们的和.按照这个规律可以将这个表继续往下写.

该表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，而他是摘录自北宋时期数学家贾宪著的《开方作法本源》中的“开方作法本源图"，因而人们把这个表叫做杨辉三角或贾宪三角，在欧洲这个表叫做帕斯卡三角形.帕斯卡（B.Pascal，1623—1662）是1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年.

(1)、应用规律：①直接写出

(a + b)^{4}

的展开式，

(a + b)^{4} =

；

② $(a + b)^{6}$ 的展开式中共有项，所有项的系数和为；

(2)、代数推理：已知

m

为整数，求证：

(m + 3)^{3} - (m - 3)^{3}

能被18整除．

查看试题解析

10. 阅读下列材料，解答下面的问题：
杨辉三角是我国南宋数学家杨辉发现的，利用杨辉三角可以很方便地写出两项多项式的 $n$ 次方的展开式.杨辉三角中的每一行的数分别对应两项多项式 $n$ 次方展开式中的各项系数.例如： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，右边的系数1、2、1是杨辉三角中第三行的三个数，又如： ${(a + b)}^{3} = a^{2} + 3 a^{2} b + 3 a b^{2} + b^{3}$ 中右边各项系数1、3、3、1是杨辉三角中第四行的四个数.根据这个规律，试解决下列问题：

(1)、试写出下一个展开式： ${(a + b)}^{4} =$ .

(2)、求 ${(2 x - 1)}^{3}$ 的展开式.

(3)、若 ${(3 x - 2)}^{n} = a_{n} x^{n} + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + \dots + a_{2} x^{2} + a_{1} x + a_{0}$ ，求 $a_{n} + a_{n - 1} + a_{n - 2} + \dots + a_{2} + a_{1} + a_{0}$ 的值.

查看试题解析
11. 杨辉三角形，又称贾宪三角形，帕斯卡三角形，是二项式系数在三角形中的一种几何排列，在我国南宋数学家杨所著的《详解九章算术》（1261年）一书中用如图的三角形解释二项和的乘方规律
（a+b）¹＝a+b

（a+b）²＝a²+2ab+b²

（a+b）³＝（a+b）（a²+2ab+b²）＝a³+3a²b+3ab²+b³

（a+b）⁴＝（a+b）（a³+3a²b+3ab²+b³）＝a⁴+4a³b+6a²b²+4ab³+b⁴

“杨辉三角”里面蕴藏了许多的规律

(1)、找出其中各项字母之间的规律以及各项系数之间的规律各一条；

(2)、直接写出（a+b）⁶展开后的多项式；

(3)、运用：若今天是星期四，经过8⁴天后是星期，经过8¹⁰⁰天后是星期．

查看试题解析