圆锥和圆柱的计算—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 若一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角为（　　）

A、120° B、180° C、240° D、300°

查看试题解析
2. 圆锥的底面圆的周长是4π cm，母线长是6 cm，则该圆锥的侧面展开图的圆心角的度数是（）

A、40° B、80° C、120° D、150°

查看试题解析
3. 如图，AB是圆锥的母线，BC为底面直径，已知BC=6cm，圆锥的侧面积为 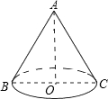$15 π$ ，则 $c o s ∠ A B O$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{3}$

查看试题解析
4. 已知圆柱体的底面半径为 $3 c m$ ，高为 $4 c m$ ，则圆柱体的侧面积为（）.

A、 $24 π c m^{2}$ B、 $36 π c m^{2}$ C、 $12 c m^{2}$ D、 $24 c m^{2}$

查看试题解析
5. 如图是农村常搭建的横截面为半圆形的全封闭塑料薄膜蔬菜大棚.如果不考虑塑料薄膜埋在土里的部分，那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是（）

A、 $64 π m^{2}$ B、 $72 π m^{2}$ C、 $68 π m^{2}$ D、 $80 π m^{2}$

查看试题解析
6. “云南十八怪”中第二怪“摘下斗笠当锅盖”，是指云南以江鞭草、山锅盖草、斑茅草和嫩竹篾片、篾丝编织成锅盖，形似斗笠，用斗笠锅盖做饭煮菜，透气保温，做出来的饭菜清香可口．如图，斗笠锅盖可以近似看为一个圆锥，若一个斗笠锅盖的底面直径为60cm，高度为40cm，则该斗笠锅盖的表面积大约为（）

A、725πcm² B、1500πcm² C、300 $\sqrt{13}$ πcm² D、600 $\sqrt{13}$ πcm²

查看试题解析
7. 已知一个圆柱的全面积是其侧面积的 $\frac{3}{2}$ 倍，且这个圆柱的全面积是 $72 π$ ，则该圆柱的底面半径 $r$ 为.

查看试题解析
8. 若圆锥的高为 $8 cm$ ，母线长为 $10 cm$ ，则这个圆锥的侧面展开图的弧长是 $cm$ ．（结果保留π）

查看试题解析
9. 如图，有 $A, B, C, D$ 四种型号的铁皮，从中选两种，正好可以制作成一个无盖圆柱形水桶(不计接头).

(1)、你认为可以选择哪两种型号的铁皮?

(2)、所制作水桶的容积是多少?

查看试题解析
10. 妈妈给圆柱形的玻璃杯（底面直径16cm，高20cm）做了一个布套（包住侧面）

(1)、求出至少用布料多少平方厘米？

(2)、求这个杯子最多可以盛水多少立方厘米？

查看试题解析
11. 如图1，在等腰三角形ABC中，∠BAC=120°，AD是∠BAC的平分线，且AD=6，以点A为圆心，AD的长为半径画 $\overset{⌢}{E F}$ ，交AB于点E，交AC于点F．

(1)、求由 $\overset{⌢}{E F}$ 及线段FC，CB，BE围成图形(图1中阴影部分)的面积(结果保留π)．

(2)、如图2，将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h．

查看试题解析
12. 如图，粮仓的顶部是圆锥形，这个圆锥的底面圆的半径为4m，高为3m.

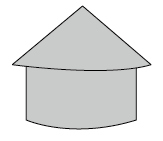(1)、求这个圆锥的母线长；

(2)、为了防雨，需要在它的顶部铺上油毡，所需油毡的面积至少是多少？（π取3.14，结果精确到1m²）

查看试题解析

二、能力提升

13. 如图所示，把矩形纸片ABCD分割成正方形纸片AFED和矩形纸片EFBC后，分别裁出扇形ADF和半径最大的圆，恰好能做成一个圆锥的侧面和底面，则AD与AB的比值为（）

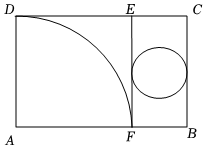A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{6}}{4}$

查看试题解析
14. 有一个装有某种液体的圆柱体容器，底面半径为4cm，高为12cm．小强不小心碰倒容器，当容器水平静置时其截面如图所示，其中圆心O到液面AB的距离为2cm，若将该容器扶正竖直放置，则容器内液体的高度为（）

A、 $\frac{4 π - \sqrt{3}}{π}$ B、 $\frac{8 π - 6 \sqrt{3}}{π}$ C、 $\frac{4 π - 3 \sqrt{3}}{12 π}$ D、 $\frac{4 π - 3 \sqrt{3}}{π}$

查看试题解析
15. 如图，在半径为 $\sqrt{2}$ 的圆形纸片中，剪一个圆心角为 $9 0^{°}$ 的最大扇形(阴影部分)，将此扇形围成一个无底的圆锥(不计接头)，则圆锥底面半径为.

查看试题解析
16. 如图，在矩形纸片 $A B C D$ 中， $A D$ 长为 $30 cm$ ，把它分割成正方形纸片 $A B F E$ 和矩形纸片 $E F C D$ 后，分别裁出扇形 $E F B$ 和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则围成的圆锥的表面积为．

查看试题解析
17. 王明用长40cm，宽20cm的两张长方形纸围成了甲、乙两个圆柱（如图，粘接处重叠部分不计），再给每个圆柱配上一个底面，做成了两个圆柱形容器．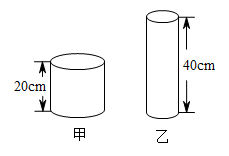

(1)、甲、乙两个圆柱谁的体积大？先提出你的猜想；

(2)、如何验证你的猜想？请你设计一个验证方案．（只需设计方案，写出主要步骤，不需要列式计算．）

查看试题解析
18. 如图，在正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：

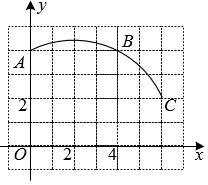(1)、利用网格确定该圆弧所在圆的圆心D点的位置，则D点坐标为；

(2)、连接AD、CD，则⊙D的半径为(结果保留根号)，∠ADC的度数为；

(3)、若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面半径.(结果保留根号).

查看试题解析

三、拓展创新

19. 综合与实践
主题：制作圆锥形生日帽．
素材：一张圆形纸板、装饰彩带．
步骤1：如图1，将一个底面半径为r的圆锥侧面展开，可得到一个半径为l、圆心角为 $n °$ 的扇形．制作圆锥形生日帽时，要先确定扇形的圆心角度数，再度量裁剪材料．
步骤2：如图2，把剪好的纸板粘合成圆锥形生日帽．
在制作好的生日帽中， $A B = 6 c m$ ， $l = 6 c m$ ， C是 $P B$ 的中点，现要从点A到点C再到点A之间拉一条装饰彩带，求彩带长度的最小值．

查看试题解析
20. 【贴士】等积变形指的是图形的面积相同或物体体积相同而形状发生变化的一种变形。我们可以利用这种变形解决生产和日常生活中的实际问题.
【链接】现有长、宽、高分别为25cm、20cm、15cm的长方体容器（如图甲），另有高为15cm的圆柱形容器（如图乙）（π取3，容器的厚度不计）.

(1)、若长方体容器中已有水高9cm，现把全部水倒入圆柱形容器（图乙）中，刚好倒满，求此圆柱形容器的底面半径。

(2)、若在长方体容器中注满水，并把水先倒满若干个边长为10cm的立方体容器（图丙），再将剩余的水全部倒入圆柱形容器（图乙）中，水不能溢出，这样的操作方案有若干种，请给出其中的两种方案，并填写下表。

方案一
方案二
立方体容器个数


圆柱形容器内水的高度（cm)



查看试题解析

	方案一	方案二
立方体容器个数
圆柱形容器内水的高度（cm)