几何体的展开图—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 下面图形中，是直三棱柱的表面展开图的是( )

A、 B、 C、 D、

查看试题解析
2. 如图，这是一个正方体的表面展开图，把展开图折叠成正方体后，“城”字对面的字是（）

A、文 B、明 C、典 D、范

查看试题解析
3. 图是一个多面体的表面展开图，每个面都标注了数字．若多面体的底面是面③，则多面体的上面是( )

A、面① B、面② C、面⑤ D、面⑥

查看试题解析
4. 下列图形中，不是立方体的表面展开图的是( )

A、 B、 C、 D、

查看试题解析
5. 下列图形中，属于长方体的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
6. 一个长方体的表面展开图如图所示，将其折叠成长方体，所得的立体图形是( )

A、 B、 C、 D、

查看试题解析
7. 如图，这是一正方体的表面展开图．将其折叠成正方体后，与顶点 $K$ 距离最远的顶点是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
8. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
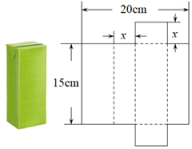9. 如图是一个长方体的表面展开图(由6个矩形组成)，请解答下列问题．

(1)、如果A面在长方体的底部，那么字母面在上面．

(2)、如果F面在长方体的前面，B面在左面，那么字母面在上面．

(3)、如果矩形A的短边为 $1 dm$ ，矩形B的长边为 $3dm$ ，矩形D的短边为 $2dm$ ．求出这个长方体的体积V．

查看试题解析

二、能力提升

10. 下面各图是圆柱的展开图的是(π取3.14)（）

A、 B、 C、 D、

查看试题解析
11. 图①为图②直三棱柱的表面展开图，其中AE，BF，CG，DH是侧棱.若图①中，AD=10，CD=2，则AB的长度可能是( )

A、2. B、3. C、3.5. D、5.

查看试题解析
12. 如图所示，点A，B是正方体上的两个顶点，将正方体按图中所示方式展开，则在展开图中B点的位置为（）

A、B₁ B、B₂ C、B₃ D、B₄

查看试题解析
13. 将如图形状的纸片折叠，可以围成的几何体的名称是，原几何体相对的两个面上的数之和最大是.

查看试题解析
14. 一个长方体的展开图如图所示，每个面分别标上的了1﹣6六个数字（数字在长方体的内侧），已知3、5、6三面面积之和是 $63 {cm}^{2}$ ，且5号面是一个边长3厘米的正方形．如果2号面是长方体底面，那么号面是长方体上面，这样围成长方体后每相连两个面上的数字之和是质数（可重复）的有组，这个长方体的体积是 ${cm}^{3}$ ．

查看试题解析
15. 在如图所示的六个方格中，分别填入-2；4； $- \frac{1}{2}$ ；8； $\frac{1}{4}$ ； $\frac{1}{8}$ ，使围成正方体后相对两面的两个数互为倒数．

查看试题解析
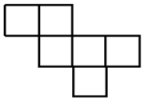16. 如图，在边长为120cm的正方形铁皮ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体工艺盒（A，B，C，D四个顶点正好重合于上底面一点）.已知点M，N在CD边上，且是被剪去的一个等腰直角三角形斜边的两个端点，设CM＝DN＝x（cm）.

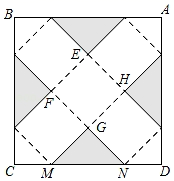(1)、若折成的包装盒恰好是个正方体，求这个工艺盒的体积；

(2)、当x取何值时，工艺盒的四个侧面面积和S最大，最大值为多少？

查看试题解析

三、拓展创新

17. 李明同学设计了某个产品的正方体包装盒如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．

(1)、共有_______种弥补方法；

(2)、任意画出一种成功的设计图（在图中补充）；

(3)、在你帮忙设计成功的图中，要把 $- 10$ ， 8，10， $- 12$ ， $- 8$ ， 12这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加等0（直接在图中填上）

查看试题解析

18. 根据以下素材，探索完成任务。

圆柱体外包装的材料损耗率问题研究
素材1	厂商在生产产品时，对产品外包装的材料，通常要考虑尽可能地合理利用，减少浪费。圆柱体形状的物品，它的外包装盒通常都是长方体，且上下底面为正方形。
素材2	设计产品外包装时，我们把裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率。一种材料利用率较高的裁剪方式如图所示，采用正方形纸板裁剪，只需剪掉四条边上的四个小三角形。按这种方式包装一个底面直径为2，高为1的圆柱体(接缝处的材料损耗不计)，损耗率只有 $\frac{2}{18}$ ≈11.1%．
	问题解决
任务1	现采用一张边长为4 $\sqrt{2}$ cm的正方形纸，按如图所示的裁剪方式剪掉各边上的四个三角形后，可恰好无缝地做成一个圆柱体的外包装盒，设圆柱体的底面半径为r，则它的高h= ▲ (用r的代数式表示)
任务2	在上图中，若已知该圆柱体外包装盒的材料损耗率为16%，求这个圆柱体的底面半径r
任务3	现利用两块同样大小的正方形纸板，按如图方式裁剪后，可包装两个高分别为4和2的圆柱体，发现这两个圆柱体的体积恰好相等．求第一个圆柱体的底面半径．(圆柱体的体积=底面积×高)

查看试题解析

19.

如何利用闲置纸板箱制作储物盒
素材 1	如图1是小琴家需要设置储物盒的区域，该区域可以近似看成一个长方体，底面尺寸如图2所示.
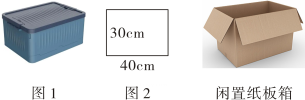
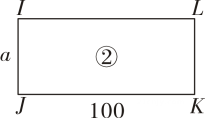
素材 2	如图3、图4是利用闲置纸板箱拆解出的①，②两种一边均为a(cm)(a<50)的矩形纸板.
	纸板①(单位：cm)			纸板②(单位：cm)

	小琴分别将纸板①和②以不同的方式制作储物盒.
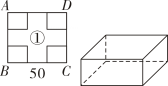
	纸板①的制作方式			纸板②的制作方式
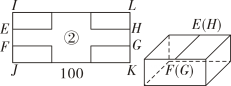
	裁去角上4个相同的小正方形，折成一个无盖长方体储物盒.			将纸片四个角裁去4个相同的小矩形，折成一个有盖的长方体储物盒。
目标 1	熟悉材料			⑴若按照纸板①的制作方式制成的储物盒恰好完全放入储物区域，则长方形纸板的宽a= cm.
目标 2		利用目标1计算所得的数据a，进行进一步探究.
		初步应用	⑵按照纸板①的制作方式，为了更方便地放入或取出储物盒，盒子四周需要留出一定的空间，当储物盒的底面积是936cm²时，求储物盒的容积.
		储物收纳	⑶按照纸板②的制作方式制作储物盒，EF和HG两边恰好重合且无重叠部分，盒子的底面积为702cm².家里一个玩具机械狗的尺寸如图所示，请通过计算判断该机械狗能否完全放入储物盒.

查看试题解析

20. 研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．
阅读材料
立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．例如，正方体 $A B C D - A^{'} B^{'} C^{'} D^{'}$ (图①)，因为在平面 $A A^{'} C^{'} C$ 中， $C C^{'} ∥$ $A A^{'} ， A A^{'}$ 与 $A B$ 相交于点 $A$ ，所以直线 $A B$ 与 $A A^{'}$ 所成的 $∠ B A A^{'}$ 就是既不相交也不平行的两条直线 $A B$ 与 $C C^{'}$ 所成的角．

(1)、解决问题
如图①，已知正方体 $A B C D -$ $A^{'} B^{'} C^{'} D^{'}$ ，求既不相交也不平行的两直线 $B A^{'}$ 与 $A C$ 所成角的大小．

(2)、如图 ②， $M ， N$ 是正方体相邻两个面上的点．
①如图 K27-16 的甲、乙、丙三个图形中，只有一个图形可以作为图②的展开图，这个图形是 ▲
②在所选正确展开图中，若点 $M$ 到 $A B ， B C$ 的距离分别是 2 和 5 ，点 $N$ 到 $B D ， B C$ 的距离分别是 4 和 $3 ， P$ 是 $A B$ 上一动点，求 $P M + P N$ 的最小值．

查看试题解析