三角形的内切圆与内心—浙教版数学九(下)知识点训练
试卷更新日期:2024-12-01 类型:复习试卷
一、基础夯实
-
1. 直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( )A、12 B、14 C、16 D、182. 已知正三角形的内切圆半径为 , 则它的边长为( )A、 B、 C、 D、3. 如图,内切于 , 切点分别为D,E,F,连结OE,OF,DE,DF.若 , 则等于( )
 A、 B、 C、 D、4. 在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点 , , 上,他们在玩抢凳子的游戏,要在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最恰当的位置是的( )A、三条高的交点 B、重心 C、三条角平分线的交点 D、外心5. 依据圆规作图的痕迹,可以用没有刻度的直尺确定的内心的是( )A、
A、 B、 C、 D、4. 在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点 , , 上,他们在玩抢凳子的游戏,要在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最恰当的位置是的( )A、三条高的交点 B、重心 C、三条角平分线的交点 D、外心5. 依据圆规作图的痕迹,可以用没有刻度的直尺确定的内心的是( )A、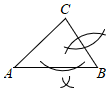 B、
B、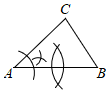 C、
C、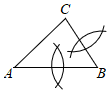 D、
D、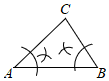 6. 如图,是的内心.若 , 则的度数是;若 , 则的度数是.
6. 如图,是的内心.若 , 则的度数是;若 , 则的度数是. 7. 如图,O为△ABC的外心,I为△ABC的内心.若∠BOC=140°,则∠BIC=
7. 如图,O为△ABC的外心,I为△ABC的内心.若∠BOC=140°,则∠BIC= 8. 已知:如图,在等腰三角形ABC中,是腰BC上的一点,的内切圆分别与边AD,BC,AC相切于点E,F,G.求证:.
8. 已知:如图,在等腰三角形ABC中,是腰BC上的一点,的内切圆分别与边AD,BC,AC相切于点E,F,G.求证:. 9. 如图,已知 , 用直尺和圆规作的内切圆.
9. 如图,已知 , 用直尺和圆规作的内切圆. 10.
10.如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠A=70°,求∠FDE.

二、能力提升
-
11. 如图,四边形为矩形,点在边上, , 与四边形的各边都相切,的半径为 , 的内切圆半径为 , 则的值为( )
 A、 B、 C、 D、12. 如图,点为的内心,连接并延长交的外接圆于点 , 交于点 , 若 , 则的值为( )
A、 B、 C、 D、12. 如图,点为的内心,连接并延长交的外接圆于点 , 交于点 , 若 , 则的值为( ) A、5 B、6 C、7 D、813. 点是的外心,也是的内心,若 , 则的度数是( )
A、5 B、6 C、7 D、813. 点是的外心,也是的内心,若 , 则的度数是( ) A、80° B、90° C、100° D、110°14. 如图,是的内切圆,切点分别是D,E,F.若 , 则的面积为.
A、80° B、90° C、100° D、110°14. 如图,是的内切圆,切点分别是D,E,F.若 , 则的面积为. 15. 已知,如图,为的直径,内接于 , 点P是的内心,延长交于点D,连接.
15. 已知,如图,为的直径,内接于 , 点P是的内心,延长交于点D,连接. (1)、求证:;(2)、已知的半径是 , , 求的长.16. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.
(1)、求证:;(2)、已知的半径是 , , 求的长.16. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.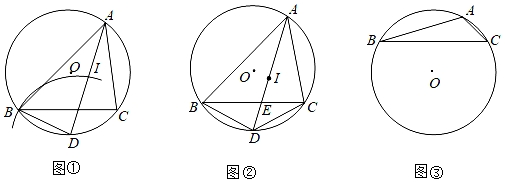 (1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证:;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.
(1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证:;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.三、拓展创新
-
17. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=( )
 A、4π B、3π C、2π D、π18. 把圆分成等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形.如图,的半径是 , 分别求它的外切正三角形、外切正方形、外切正六边形的边长.
A、4π B、3π C、2π D、π18. 把圆分成等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形.如图,的半径是 , 分别求它的外切正三角形、外切正方形、外切正六边形的边长. 19. 【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.
19. 【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=ar+br+cr=(a+b+c)r.
∴r= .
(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC各边分别相切于D、E和F,已知AD=3,BD=2,求r的值.
 20. 阅读以下材料,并按要求完成相应地任务:
20. 阅读以下材料,并按要求完成相应地任务:

莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,
任务:
(1)、观察发现: , (用含R,d的代数式表示);(2)、请判断BD和ID的数量关系,并说明理由;(3)、请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;(4)、应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为cm.