切线长定理—浙教版数学九(下)知识点训练
试卷更新日期:2024-12-01 类型:复习试卷
一、基础夯实
-
1. 如图,PA,PB是的两条切线,A,B为切点,直线OP交于点D,E,交AB于点.有下列结论:
①;②;③;④.其中正确的有( )
 A、①③④. B、②③④. C、①②③. D、①②④.2. 如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若△PCD的周长等于3,则PA的值是( )
A、①③④. B、②③④. C、①②③. D、①②④.2. 如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若△PCD的周长等于3,则PA的值是( ) A、 B、 C、 D、3. 如图,△ABC是一张周长为18cm的三角形纸片,BC=5cm,⊙O是它的内切圆,小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A、 B、 C、 D、3. 如图,△ABC是一张周长为18cm的三角形纸片,BC=5cm,⊙O是它的内切圆,小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )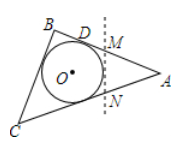
A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化4. 如图,AD , AE分别是⊙O的切线,D , E为切点,BC切⊙O于F , 交AD , AE于点B , C , 若AD=8.则三角形ABC的周长是( )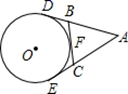 A、8 B、10 C、16 D、不能确定5. 如图,的内切圆与、、分别相切于点D、E、F且 , 则的周长为( ).
A、8 B、10 C、16 D、不能确定5. 如图,的内切圆与、、分别相切于点D、E、F且 , 则的周长为( ). A、7 B、14 C、10 D、46. 如图,PA、PB切⊙O于A、B,点C在 上,DE切⊙O于C交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是 .
A、7 B、14 C、10 D、46. 如图,PA、PB切⊙O于A、B,点C在 上,DE切⊙O于C交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是 . 7. 如图,PA,PB,CD都是的切线,切点分别为A,B,E.若的周长为 , 求:
7. 如图,PA,PB,CD都是的切线,切点分别为A,B,E.若的周长为 , 求: (1)、PA的长.(2)、∠COD的度数.8. 如图,在Rt△ABC中,∠C=90°,△ABC的内切圆⊙O切AB于点D,切BC于点E,切AC于点F,AD=4,BD=6,求Rt△ABC的面积.
(1)、PA的长.(2)、∠COD的度数.8. 如图,在Rt△ABC中,∠C=90°,△ABC的内切圆⊙O切AB于点D,切BC于点E,切AC于点F,AD=4,BD=6,求Rt△ABC的面积.
二、能力提升
-
9. 如图,⊙O与正方形ABCD的两边AB,AD相切,且DE与⊙O相切于E点.若⊙O的半径为4,且AB=10,则DE的长度为( )
 A、5 B、6 C、 D、10. 如图, 中, , ,它的周长为 若 与 , , 三边分别切于 , , 点,则 的长为( )
A、5 B、6 C、 D、10. 如图, 中, , ,它的周长为 若 与 , , 三边分别切于 , , 点,则 的长为( )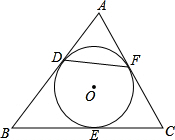 A、2 B、3 C、4 D、511. 如图,PA和PB是⊙O的两条切线,A,B为切点,点D在AB上,点E,F分别在线段PA和PB上,且AD=BF,BD=AE.若∠P=α,则∠EDF的度数为( )
A、2 B、3 C、4 D、511. 如图,PA和PB是⊙O的两条切线,A,B为切点,点D在AB上,点E,F分别在线段PA和PB上,且AD=BF,BD=AE.若∠P=α,则∠EDF的度数为( )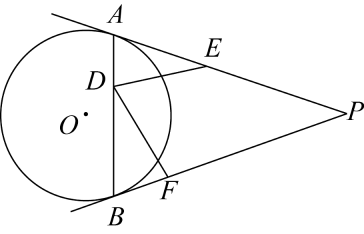 A、90°-α B、α C、2α D、90°-α12. 如图, , 切于、两点,切于点 , 分别交 , 于 , , , 若的半径为r,的周长等于 , 则的值是( )
A、90°-α B、α C、2α D、90°-α12. 如图, , 切于、两点,切于点 , 分别交 , 于 , , , 若的半径为r,的周长等于 , 则的值是( ) A、 B、 C、 D、13. 《九章算术》中记载:“今有勾六步,股八步.问勾中容圆径几何?”译文:今有一个直角三角形,勾(短直角边)长为6步,股(长直角边)长为8步,则该直角三角形内切圆的直径是等于步.14. 如图,为的直径, , 分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若 , 则线段的长为 .
A、 B、 C、 D、13. 《九章算术》中记载:“今有勾六步,股八步.问勾中容圆径几何?”译文:今有一个直角三角形,勾(短直角边)长为6步,股(长直角边)长为8步,则该直角三角形内切圆的直径是等于步.14. 如图,为的直径, , 分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若 , 则线段的长为 . 15. 如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是 , 量角器与刻度尺接触点在刻度尺上的读数是 , 量角器与三角板的接触点为B .
15. 如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是 , 量角器与刻度尺接触点在刻度尺上的读数是 , 量角器与三角板的接触点为B . (1)、 .(2)、该量角器的直径长为 . (结果保留根号)16. 如图,⊙O的直径AB=2,AM、BN是它的两条切线,CD与⊙O相切于点E,与BN、AM交于点C、D,设AD=x,BC=y.
(1)、 .(2)、该量角器的直径长为 . (结果保留根号)16. 如图,⊙O的直径AB=2,AM、BN是它的两条切线,CD与⊙O相切于点E,与BN、AM交于点C、D,设AD=x,BC=y.(1)求证:AM∥BN.
(2)求y关于x的函数关系式.
(3)若x、y是关于t的方程的两根,且xy= , 求x、y的值.
 17. 如图,以矩形ABCD的边CD为直径作 , 点E是AB的中点,连接CE交于点F,连接AF并延长交BC于点H.
17. 如图,以矩形ABCD的边CD为直径作 , 点E是AB的中点,连接CE交于点F,连接AF并延长交BC于点H. (1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是的切线;(3)、若 , , 求AH的长.
(1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是的切线;(3)、若 , , 求AH的长.三、拓展创新
-
18. 我们给出以下定义:如图(1)若点P在不大于的的内部,作于点Q,于点I,则称为点P与的“点角距离”记作.如图(2)在平面直角坐标系中,x、y的正半轴组成的 , O为坐标原点.
 (1)、如图(2)点 , 则;(2)、若点B为内一点, , 以点B为圆心r为半径作圆,与x轴、y轴均相切,求点B的坐标;(3)、已知点.
(1)、如图(2)点 , 则;(2)、若点B为内一点, , 以点B为圆心r为半径作圆,与x轴、y轴均相切,求点B的坐标;(3)、已知点.①已知点D的坐标为 , 求的解析式和的值.
②已知点在的内部, , 当s为大于0的任意实数时,代数式(m为常数)的值为定值,求m的值及该定值.