切线的判定与性质—浙教版数学九(下)知识点训练
试卷更新日期:2024-12-01 类型:复习试卷
一、基础夯实
-
1.
如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
 A、AB=4,AT=3,BT=5 B、∠B=45°,AB=AT C、∠B=55°,∠TAC=55° D、∠ATC=∠B2. 如图,边长为的小正方形网格中,点在格点上,过三点的圆交于点 , 则的正切值是( )
A、AB=4,AT=3,BT=5 B、∠B=45°,AB=AT C、∠B=55°,∠TAC=55° D、∠ATC=∠B2. 如图,边长为的小正方形网格中,点在格点上,过三点的圆交于点 , 则的正切值是( ) A、 B、2 C、 D、3. 如图所示,在△ABC中,O是AB边上的点,以O为圆心,OB的长为半径的⊙O与AC相切于点D,BD平分∠ABG,AD=OD,AB=12,则CD的长是( )
A、 B、2 C、 D、3. 如图所示,在△ABC中,O是AB边上的点,以O为圆心,OB的长为半径的⊙O与AC相切于点D,BD平分∠ABG,AD=OD,AB=12,则CD的长是( ) A、2 B、2 C、3 D、44. 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连结AD,若∠DAC=78°,则∠ADO=( )
A、2 B、2 C、3 D、44. 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连结AD,若∠DAC=78°,则∠ADO=( ) A、70° B、64° C、62° D、51°5. 如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连结AC并延长,交BD于点D,连结OC,BC,若∠BOC=50°,则∠D的度数为( )
A、70° B、64° C、62° D、51°5. 如图,AB是⊙O的直径,BD与⊙O相切于点B,点C是⊙O上一点,连结AC并延长,交BD于点D,连结OC,BC,若∠BOC=50°,则∠D的度数为( ) A、50° B、55° C、65° D、75°6. 如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2 , 那么∠AOB等于( )
A、50° B、55° C、65° D、75°6. 如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2 , 那么∠AOB等于( ) A、90° B、100° C、110° D、120°7. 如图,在矩形ABCD中,BC=6,AB=3.⊙O是以BC为直径的圆,则直线AD与⊙O的位算关系是
A、90° B、100° C、110° D、120°7. 如图,在矩形ABCD中,BC=6,AB=3.⊙O是以BC为直径的圆,则直线AD与⊙O的位算关系是 8. 如图,的半径为5,PA切于点.若 , 则切线长(结果保留根号).
8. 如图,的半径为5,PA切于点.若 , 则切线长(结果保留根号). 9. 如图,的内接四边形中, , 是它的对角线,的中点是的内心.
9. 如图,的内接四边形中, , 是它的对角线,的中点是的内心.
求证:
(1)、是的外接圆的切线;(2)、 .10. 如图,AB是⊙O的直径,点C是弧BE中点,AE⊥CD于点D,延长DC,AB交于点F,已知AD=4,FC=FB. (1)、求证:CD与⊙O相切.(2)、求⊙O的半径.
(1)、求证:CD与⊙O相切.(2)、求⊙O的半径.二、能力提升
-
11. 如图,在等边三角形ABC中,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,F是AC上的点,则下列说法中错误的是( )
 A、若EF⊥AC,则EF是⊙O的切线 B、若EF是⊙O的切线,则EF⊥AC C、若BE=EC,则AC是⊙O的切线 D、若BE=EC,则AC是⊙O的切线12. 某校举办校庆晚会,其主舞台为一圆形舞台,圆心为O.A,B是舞台边缘上两个固定位置,由线段AB及优弧围成的区域是表演区.若在A处安装一台某种型号的灯光装置,其照亮区域如图1中阴影所示.若在B处再安装一台同种型号的灯光装置,恰好可以照亮整个表演区,如图2中阴影所示
A、若EF⊥AC,则EF是⊙O的切线 B、若EF是⊙O的切线,则EF⊥AC C、若BE=EC,则AC是⊙O的切线 D、若BE=EC,则AC是⊙O的切线12. 某校举办校庆晚会,其主舞台为一圆形舞台,圆心为O.A,B是舞台边缘上两个固定位置,由线段AB及优弧围成的区域是表演区.若在A处安装一台某种型号的灯光装置,其照亮区域如图1中阴影所示.若在B处再安装一台同种型号的灯光装置,恰好可以照亮整个表演区,如图2中阴影所示
若将灯光装置改放在如图3所示的点M,N或P处,能使表演区完全照亮的方案可能是( )
①在M处放置2台该型号的灯光装置②在M,N处各放置1台该型号的灯光装置③在P处放置2台该型号的灯光装置
A、① B、①② C、②③ D、①②③13. 如图,射线QN与等边三角形ABC的两边AB,BC分别交于点M,N,且AC.动点从点出发,沿射线QN以每秒的速度向右移动,设点运动的时间为 , 当以点为圆心,为半径的圆与的边相切(切点在边上)时,请写出可取的所有值:. 14. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
14. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).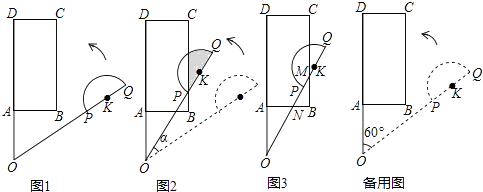
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
三、拓展创新
-
15. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( )
 A、
A、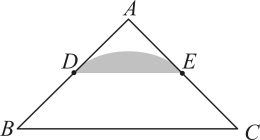 B、
B、 C、
C、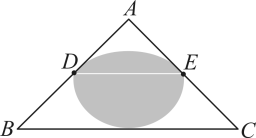 D、
D、 16. 请阅读下列材料,并完成相应的任务.
16. 请阅读下列材料,并完成相应的任务.人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.

如图②,AB与⊙O相切于点A , 当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D , 在 上任取一点E , 连接EC , ED , EA , 则∠CED=∠CAD.
…
任务:
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、如图③,AB与⊙O相切于点A.当圆心O在∠BAC的外部时,请写出弦切角定理的证明过程.