解直角三角形之背靠背模型—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、选择题

1. 在 $△ A B C$ 中， $B C = \sqrt{3} + 1 ， ∠ B = 45^{\circ} ， ∠ C = 30^{\circ}$ ，则 $△ A B C$ 的面积为（）

A、 $\frac{\sqrt{3} - 1}{2}$ B、 $\frac{\sqrt{3}}{2} + 1$ C、 $\frac{\sqrt{3} + 1}{2}$ D、 $\sqrt{3} + 1$

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ B$ 和 $∠ C$ 都是锐角，若 $∠ B = α, ∠ C =$ $β$ ，则（）

A、 $A B \cdot c o s β = A C \cdot c o s α$ B、 $A B \cdot s i n α = A C \cdot c o s β$ C、 $A B \cdot s i n α = A C \cdot s i n β$ D、 $A B \cdot s i n β = A C \cdot s i n α$

查看试题解析
3. 如图所示，热气球的探测器显示，从热气球 $A$ 处看一栋楼顶部 $B$ 处的仰角为 $30 °$ ，看这栋楼底部 $C$ 处的俯角为 $60 °$ ，热气球 $A$ 处与楼的水平距离为 $150 m$ ，则这栋楼的高度为（）

A、 $50 \sqrt{3} m$ B、 $150 \sqrt{3} m$ C、 $200 \sqrt{3} m$ D、 $300 m$

查看试题解析
4.
如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（　　）

A、4km B、2 $\sqrt{3}$ km C、2 $\sqrt{2}$ km D、（ $\sqrt{3}$ +1）km

查看试题解析
5. 如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60海里的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离是（）

A、30海里 B、60海里 C、120海里 D、（30＋30 $\sqrt{3}$ ）海里

查看试题解析

二、填空题

6. 如图，A，B两地间隔着海岛，直线距离为100海里，已知 $B$ 地在 $A$ 地的北偏东 $3 0^{°}$ 的方向上，货轮从 $A$ 地出发向正北方向航行到达灯塔 $C$ 处，再从灯塔 $C$ 沿北偏东 $7 5^{°}$ 方向航行到达 $B$ 地，则货轮从 $A$ 地出发到达灯塔 $C$ 航行的距离为海里(结果保留根号).

查看试题解析
7. 如图，河宽CD为100 $\sqrt{3}$ 米，在C处测得对岸A点在C点南偏西30°方向、对岸B点在C点南偏东45°方向，则A、B两点间的距离是米.（结果保留根号）

查看试题解析

三、解答题

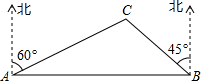
8. 如图，A，B两市相距150km，国家级风景区中心C位于A市北偏东 $60^{°}$ 方向上，位于B市北偏西 $45^{°}$ 方向上.已知风景区是以点C为圆心、50km为半径的圆形区域.为了促进旅游经济发展，有关部门计划修建连接A，B两市的高速公路，高速公路AB是否穿过风景区？通过计算加以说明.（参考数据： $\sqrt{3} \approx 1.73$ ）

查看试题解析
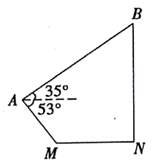
9. 如图，一架无人机在距离地面高度为14.3米的点A处，测得地面上点M的俯角为
53°，这架无人机沿仰角为350的方向飞行了56米到达点B，恰好在地面上点N的正

上方，M，N在同一水平线上.求M，N两点之间的距离. (结果精确到1米.参考数据： sin53°≈0.80 ，cos53°≈0.60，tan53°≈1 .33， sin35°≈0.57，cos35°≈0.82，

tan35°≈0.70 )

查看试题解析
10. 如图，为了修建跨江大桥，需要利用数学方法测量江的宽度 $A B$ ．飞机上的测量人员在C处测得A，B两点的俯角分别为 $45 °$ 和 $30 °$ ．若飞机离地面的高度 $C D$ 为 $1000 m$ ，且点D，A，B在同一水平直线上，试求这条江的宽度 $A B$ （结果精确到 $1 m$ ，参考数据： $\sqrt{2} \approx 1.4142 ， \sqrt{3} \approx 1.7321$ ）

查看试题解析
11. 如图，某防洪大坝的横截面是梯形ABCD，迎水坡CD的坡角为30°，坝顶AD宽度为2米，坝高AE为4米，背水坡AB的坡度主i=1：1.

(1)、求该堤坝的横截面积.

(2)、为更好应对可能来临的汛情，防洪指挥部决定加固堤坝，要求坝高不变，坝顶宽度增加1米，背水坡的坡度改为i=1：1.5，求加固后的堤坝的横截面积.（结果均保留根号）

查看试题解析
12. 如图，要在木里县某林场东西方向的两地之间修一条公路MN，已知C点周围200米范围内为原始森林保护区，在MN上的点A处测得C在A的北偏东45°方向上，从A向东走600米到达B处，测得C在点B的北偏西60°方向上．

(1)、MN是否穿过原始森林保护区，为什么？（参考数据： $\sqrt{3}$ ≈1.732）

(2)、若修路工程顺利进行，要使修路工程比原计划提前5天完成，需将原定的工作效率提高25%，则原计划完成这项工程需要多少天？

查看试题解析
13. 如图，在东西方向的海绵线MN上，有A，B两艘巡逻船和观测点D（A，B，D在直线MN上），两船同时收到渔船C在海绵停滞点发出的求救信号．测得渔船分别在巡逻船A，B北偏西30°和北偏东45°方向，巡逻船A和渔船C相距120海里，渔船在观测点D北偏东15°方向．（说明：结果取整数．参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

(1)、求巡逻船B与观测点D间的距离；

(2)、已知观测点D处45海里的范围内有暗礁．若巡逻船B沿BC方向去营救渔船C有没有触礁的危险？并说明理由．

查看试题解析

四、实践探究题

14. 如图

（问题背景）如图1，在△ABC中，点D在边BC上且满足∠BAD＝∠ACB，求证：BA²＝BD•BC；

（尝试应用）如图2，在△ABC中，点D在边BC上且满足∠BAD＝∠ACB，点E在边AB上，点G在AB的延长线上，延长ED交CG于点F，若3AD＝2AC，BE＝ED，BG＝2，DF＝1，求BE的长度；

（拓展创新）如图3，在△ABC中，点D在边BC上（AB≠AD）且满足∠ACB＝2∠BAD，DH⊥AB垂足为H，若 $\frac{A H}{A D} = \frac{7}{9} ， \frac{A D}{A C} = \frac{28}{27}$ ，请直接写出 $\frac{A D}{A B}$ 的值 ▲ .

查看试题解析
15. 【实践课题】测量湖边观测点A和湖心岛上鸟类栖息点P之间的距离．
【实践工具】皮尺、测角仪等测量工具
【实践活动】某班甲小组根据胡岸地形状况，在岸边选取合适的点B ．测量A ， B两点间的距离以及∠PAB和∠PBA ，测量三次取平均值，得到数据：AB＝60米，∠PAB＝79°，∠PBA＝64°．画出示意图，如图1：

(1)、【问题解决】计算A ， P两点间的距离．
（参考数据：sin64°≈0.90，sin79°≈0.98，cos79°≈0.19，sin37°≈0.60，tan37°≈0.75）

(2)、【交流研讨】甲小组回班汇报后，乙小组提出了另一种方案：
如图2，选择合适的点D ， E ， F ，使得A ， D ， E在同一条直线上，且AD＝DE ， ∠DEF＝∠DAP ，当F ， D ， P在同一条直线上时，只需测量EF即可．
乙小组的方案用到了．（填写正确答案的序号）
①解直角三角形
②三角形全等
【教师评价】甲、乙两小组的方案都很好，对于实际测量，要根据现场地形状况选择可实施的方案．

查看试题解析