解直角三角形的实际应用（4）其它类型—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 图1是一种落地晾衣架，晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示， $A B$ 和 $C D$ 分别是两根不同长度的支撑杆，其中两支脚 $O D = O B = 50 c m$ ，展开角 $∠ B O D = 7 0^{°}$ ，晾衣臂 $A O = 80 c m$ ，则支樟杆的端点 $A$ 离地面的高度 $A E$ 为（）

A、 $130 t a n 5 5^{°} c m$ B、 $130 s i n 5 5^{°} c m$ C、 $\frac{130}{t a n 5 5^{°}} c m$ D、 $\frac{130}{s i n 5 5^{°}} c m$

查看试题解析
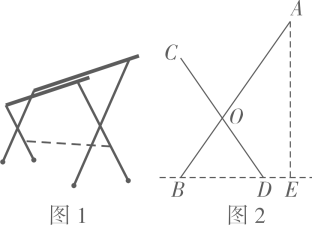2. 如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC= $α$ ， ∠ADC= $β$ ，则竹竿AB与AD的长度之比为 $($ $)$

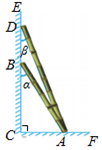A、 $\frac{t a n α}{t a n β}$ B、 $\frac{s i n β}{s i n α}$ C、 $\frac{s i n α}{s i n β}$ D、 $\frac{c o s β}{c o s α}$

查看试题解析
3. 如图是一架人字梯，已知AB＝AC＝2米，AC与地面BC的夹角为a，则两梯脚之间的距离BC为（）

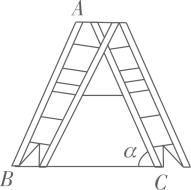A、4cos a B、4sin a C、4tan a D、 $\frac{4}{\cos a}$

查看试题解析
4. 桔槔俗称“吊杆”、“称杆”（如图1），是我国古代农用工具，始见于《墨子·备城门》，是一种利用杠杆原理的取水机械．桔槔示意图如图2所示， $O M$ 是垂直于水平地面的支撑杆， $O M = 3$ 米， $A B$ 是杠杆， $A B = 6$ 米， $O A ： O B = 2 ： 1$ ．当点 $A$ 位于最高点时， $∠ A O M = 130 °$ ．此时，点 $A$ 到地面的距离为（    ）

图1   图2

A、 $x$ 米 B、5米 C、 $(3 + 4 s i n 40 °)$ 米 D、 $(3 + \frac{4}{s i n 40 °})$ 米

查看试题解析
5. 如图钓鱼竿 $A C$ 长8m，露在水面上的鱼线 $B C$ 长 $4 \sqrt{2} m$ ，钓者想看看鱼钩上的情况，把鱼竿 $A C$ 逆时针转动15°到 $A C^{'}$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 长度是（　　）

A、3m B、 $3 \sqrt{3} m$ C、4m D、 $4 \sqrt{3} m$

查看试题解析
6. 已知图1是超市购物车，图2是超市购物车侧面示意图，测得支架AC＝80cm ， BC＝60cm ， AB ， DO均与地面平行，支架AC与BC之间的夹角∠ACB＝90°．

(1)、求两轮轮轴A ， B之间的距离；

(2)、若OF的长度为60cm ， ∠FOD＝120°，求点F到AB所在直线的距离．（结果精确到0.1）（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
7. 如图1是某住户窗户上方安装的遮阳篷，要求设计的遮阳篷既能最大限度地遮住夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内．其中 $C D$ 是垂直于墙面 $A C$ 的遮阳篷， $A B$ 表示窗户， $B C D$ 表示直角遮阳篷．如图2，通过查阅相关资料和实际测量：夏至日这一天的正午时刻太阳光线 $D A$ 与遮阳篷 $C D$ 的夹角 $∠ A D C$ 最大，且最大角 $∠ A D C = 75 °$ ；冬至日这一天的正午时刻，太阳光线 $D B$ 与遮阳篷 $C D$ 的夹角 $∠ B D C$ 最小，且最小角 $∠ B D C = 35 °$ ．（参考数据： $s i n 75 ° \approx 0.97, c o s 75 ° \approx 0.26, t a n 75 ° \approx 3.73,$ $s i n 35 ° \approx 0.57, c o s 35 ° \approx 0.83,$ $t a n 35 ° \approx 0.7$ ）

(1)、如图3，若只要求设计的遮阳篷能最大限度地遮住夏天炎热的阳光，当 $C D = 1 m$ 时，求 $A C$ 的长．

(2)、如图2，要求设计的遮阳篷能最大限度地遮住夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内．当 $A B = 1.5 m$ 时，根据上述方案及数据，求遮阳篷 $C D$ 的长．（结果精确到 $0.1 m$ ）

查看试题解析

二、能力提升

8. 如图1是装满液体的高脚杯示意图，测量发现点 $A$ 到地面 $D D^{^{'}}$ 的距离为 $29, C D = 14, A B = 10$ ，若用去一部分液体后，液面下降的高度恰好等于此时的液面EF，则 $E F =$ （）

A、9 B、8 C、6. D、5

查看试题解析
9. 如图，图①是放置在水平地面上的落地式话筒架实物图，图②是其示意图．支撑杆 $A B$ 垂直于地面 $l$ ，活动杆 $C D$ 固定在支撑杆上的点A处．若 $∠ B A D = 132 °$ ， $A B = a$ 厘米， $A D = b$ 厘米，则活动杆端点 $D$ 离地面的高度为（）

A、 $(a + b \sin 48 °)$ 厘米 B、 $(a + b \cos 48 °)$ 厘米 C、 $(a + \frac{b}{\sin 48 °})$ 厘米 D、 $(a + \frac{b}{\cos 48 °})$ 厘米

查看试题解析
10. 如图是椭圆机在使用过程中某时刻的侧面示意图，已知手柄 $A D ⊥$ 滚轮连杆AB ， $A D = 20 c m$ ， $A B = 160 c m$ ，连杆AB与底座BC的夹角为60°，则该椭圆机的机身高度（点D到地面的距离）为（）

A、 $80 \sqrt{2} c m$ B、 $80 \sqrt{3} c m$ C、 $(80 \sqrt{2} + 20) c m$ D、 $(80 \sqrt{3} + 10) c m$

查看试题解析
11. 贴春联是中国传统习俗，晓红老家有个圆形拱门，每年都会贴上长长的春联，看上去非常喜庆 $.$ 晓红用圆弧近似模拟拱门，经测量发现， $\overset{⏜}{A D B}$ 的拱高 $C D$ 和其所对的弦 $A B$ 都是 $2 m$ ， $\overset{⏜}{E B}$ 所对的圆心角是 $150 °$ ，弦 $A B$ 与春联的底端平齐， $E$ 点正好是春联外侧最高点，则春联的外侧长度大约是 $m . ($ 参考数据 $\sqrt{3} = 1.732$ ，结果按四舍五入法精确到 $0.1)$

查看试题解析
12. 新能源汽车是指采用非常规的车用燃料作为动力来源，综合车辆的动力控制和驱动方面的先进技术，形成的技术原理先进、具有新技术、新结构的汽车。如图1是某新能源汽车侧面示意图，图2是该车后备箱开起侧面示意图，具体数据如图所示(单位：cm)，且AC=BD，AF//BE，sin∠BAF=0.8，箱盖开起过程中，点A，C，F不随箱盖转动，点B，D，E绕点A沿逆时针方向转动相同角度，分别到点B'，D'，E'的位置，气簧活塞杆CD随之伸长CD'.已知直线BE⊥B'E'，CD^'= $\frac{\sqrt{17}}{3}$ CD.则CD=cm

查看试题解析
13. 如图 1 是一款重型订书机，其结构示意图如图 2 所示.其主体部分为矩形 EFGH，由支撑杆 CD 垂直固定于底座 AB 上，且可以绕点 D 旋转.压杆 MN 与伸缩片 PG 连接，点 M 在HG 上，MN 可绕点 M 旋转，PG⊥HG ，DF＝8 cm，GF=2cm，不使用时，EF $∥$ AB，G 是 PF 中点，且点 D 在 NM 的延长线上，则 MG= cm，使用时如图3，按压 MN 使得 MN $∥$ AB，此时点 F 落在 AB 上，若 CD＝2 cm，则压杆 MN 到底座 AB 的距离为 cm

查看试题解析
14. 如图是一种手机三脚架，它通过改变锁扣C在主轴AB上的位置调节三脚架的高度，其它支架长度固定不变，已知支脚DE=AB ．底座CD⊥AB ， BG⊥AB ，且CD=BG ， F是DE上的固定点，且EF：DF=2：3．

(1)、当点B ， G ， E三点在同一直线上（如图1所示）时，测得tan∠BED=2；设BC=5a ，则FG=(用含a的代数式表示)；

(2)、在(1)的条件下，若将点C向下移动24cm，则点B ， G ， F三点在同一直线上（如图2），此时点A离地面的高度是cm．

查看试题解析
15. 如图1是一种建筑行业用的小型吊机实物图，图2、图3是吊机的示意图，支架AB=150cm，吊杆 AM=200cm，∠ACB＝90°，∠BAC＝37°.

(1)、如图 2，若AM⊥AB，求点 M到直线 BC的距离；

(2)、如图3，当液压杆 DE 伸长时，此时点 M 比(1)中的点 M到直线BC 的距离升高了21cm，
求∠MAB的度数.（参考数据：sin37°≈0.6，cos37°≈0.8，sin45°≈0.7）

查看试题解析
16. 小南用一把可调节大小的活动扳手拧一枚正六边形螺丝帽（如图1），其横截面示意图如图2所示．已知活动扳手的钳口 $A B ∥ C D$ ，正六边形螺丝帽的两个顶点 $E, H$ 分别在 $A B, C D$ 上， $E F = 10$ mm， $∠ B E F = 15 °$ ．

(1)、连接 $E H$ ，求 $∠ E H C$ ；

(2)、在图2的基础上，调节活动扳手钳口大小，使得 $E F$ 与直线 $A B$ 重合， $H I$ 与直线 $C D$ 重合（如图3），请问 $A B$ 和 $C D$ 之间的距离减少了多少？（结果精确到1mm，参考数据： $sin 15 ° \approx 0.26,cos 15 ° \approx 0.97, \sqrt{3} \approx 1.73, \sqrt{2} \approx 1.41$ ）

查看试题解析

三、拓展创新

17. 根据以下素材，探索完成任务．

项目背景：太阳能是绿色能源，为了更好的推广太阳能，某厂商决定在斜坡上安装太阳能电池板，为了保证每个电池板都能有充足的光照，现需要对电池板的摆放位置进行研究．
素材一	将电池板的侧面摆放情况抽象成如图所示的数学示意图，其中第一排电池板 $A D$ 位置固定，第二排 $H G$ 位置待确定，每块电池板与坡面夹角固定不变， $D E$ ， $G M$ 所在的直线垂直于水平线 $A C$ ，坡面 $A B = 4 m$ ， $∠ B A C = 16 °$ ， $A D = H G = 100 cm$ ， $A E = 91 cm$ ， $∠ D A C = 31 °$	参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{6} \approx 2.45$
素材二	上午太阳光线与水平线的夹角 $α$ 范围为 $14 ° < α \leq 29 °$ ， $E F$ 为阴影长，为了使得太阳能电池板有充足的阳光照射，点H要落在阴影外面．
问题解决
任务一	计算角度	当 $α$ 等于 $14 °$ 时， $∠ A F D =$ ______．
任务二	探究影长	求 $D E$ 在斜坡上的阴影 $E F$ 的取值范围（精确到 $0.1 cm$ ）．
任务三	方案选择（选择其中的一种方案进行研究）	方案一：若在该斜坡上安装3排 $100 cm$ 的电池板，每一排之间的间距相同，在充分利用斜坡的情况下，电池板之间的最大间距为多少（精确到 $1 cm$ ）．方案二：若在该斜坡上安装2排电池板，电池板与坡面夹角保持不变，那么原来 $100 cm$ 长的电池板最大可以定制多长（精确到 $0.1 cm$ ）．

查看试题解析

18. 学科综合
我们在物理学科中学过：光线从空气射入水中会发生折射现象 $($ 如图 $1)$ ，我们把 $n = \frac{s i n α}{s i n β}$ 称为折射率 $($ 其中 $α$ 代表入射角， $β$ 代表折射角 $)$ ．
观察实验
为了观察光线的折射现象，设计了图 $2$ 所示的实验，即通过细管 $M N$ 可以看见水底的物块 $C$ ，但不在细管 $M N$ 所在直线上，图 $3$ 是实验的示意图，四边形 $A B F E$ 为矩形，点 $A$ ， $C$ ， $B$ 在同一直线上，测得 $B F = 12 c m$ ， $D F = 16 c m$ ．

(1)、求入射角 $α$ 的度数．

(2)、若 $B C = 7 c m$ ，求光线从空气射入水中的折射率 $n . ($ 参考数据： $s i n 53 ° \approx \frac{4}{5}$ ， $c o s 53 ° \approx \frac{3}{5}$ ， $t a n 53 ° \approx \frac{4}{3})$

查看试题解析
19. 城市雕塑“摇橹人”位于吉林市吉林大街南端的江城广场，雕塑人物以几乎倾斜倒地的姿势，用尽全身力气来摆动船橹，代表着吉林人民在湍流江水之中奋力拼搏的精神.某校数学活动小组要测量“摇橹人”的高度，张明同学带领小组成员进行此项实践活动，活动步棸记录如下：
【步骤一】设计测量方案：小组成员讨论后，画出如图①的测量草图，确定需测的几何量.
【步骤二】准备测量工具：皮尺和自制测高仪.其中测高仪 $A B C D$ （如图②）为正方形木板，在顶点 $A$ 处用细线挂一个铅锤 $M$ .
【步骤三】实地测量并记录数据：如图③，令测高仪上的顶点 $D$ ， $A$ 与“摇橹人”最高点 $E$ 在同一条直线上.通过测量得到， $∠ B A M = 36 °$ ， $A F = 20 m$ ， $F G = 1.94 m$ .
【步骤四】计算“摇橹人”高度 $E G$ .（结果精确到0.1m）（参考数据： $s i n 36 ° \approx 0.588$ ， $c o s 36 ° \approx 0.809$ ， $t a n 36 ° \approx 0.727$ ）
现在，请你结合图③和相关数据完成【步骤四】.

查看试题解析
20. 一透明的敞口正方体容器ABCD﹣A^'B^'C^'D^'装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α（∠CBE＝α，如图所示）．
探究：如图1，液面刚好过棱CD ，并与棱BB^'交于点Q ，此时液体的形状为直三棱柱，其三视图及尺寸如图②．

(1)、解决问题：CQ与BE的位置关系是， BQ的长是dm ， α＝°（注：sin49°＝cos41° $= \frac{3}{4}$ ， tan37° $= \frac{3}{4}$ ）

(2)、求液体的体积；（参考算法：直棱柱体积V液＝底面积SBCQ×高AB）

(3)、在图1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出．图3或图4是其正面示意图，若液面与棱C^'C或CB交于点P、点Q始终在棱BB^'上，设PC＝x ， BQ＝y ，分别就图3和图4求y与x的函数关系式，并写出相应的α的范围．

查看试题解析