解直角三角形的实际应用（3）方向角问题—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，为了测量一条河流的宽度，一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置，T在P的正北方向，且T在Q的北偏西70°方向，则河宽（PT的长）可以表示为（）

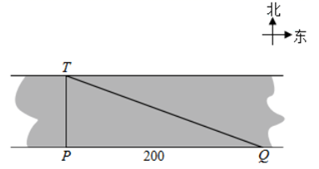A、200tan70°米 B、 $\frac{200}{\tan 70 °}$ 米 C、200sin70°米 D、 $\frac{200}{\sin 70 °}$ 米

查看试题解析
2. 南沙群岛是我国固有领土，我南海渔民要在南沙某海岛A附近进行捕鱼作业，从位于海岛A的南偏东 $30 °$ 方向、距离海岛50海里的B处出发，沿正北方向航行一段时间后，到达位于海岛A的东北方向上的C处，则渔船航行的距离为（）．

A、 $25 \sqrt{2}$ 海里 B、 $25 \sqrt{3}$ 海里 C、 $25 (\sqrt{2} + 1)$ 海里 D、 $25 (\sqrt{3} + 1)$ 海里

查看试题解析
3. 如图，在 $A$ 处测得点 $P$ 在北偏东 $6 0^{°}$ 方向上，在 $B$ 处测得点 $P$ 在北偏东 $3 0^{°}$ 方向上，若 $A B = 2$ 米，则点 $P$ 到直线 $A B$ 距离 $P C$ 为（）

A、 $3$ 米 B、 $\sqrt{3}$ 米 C、 $2$ 米 D、 $1$ 米

查看试题解析
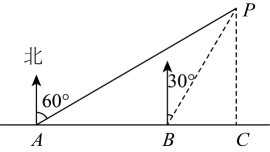4. 如图，一艘船向东航行，上午8时到达O处，测得一灯塔A在船的北偏东60°方向，且与船相距 $30 \sqrt{3}$ 海里；上午11时到达B处，测得灯塔在船的正北方向.则这艘船航行的速度为（）

A、 $45$ 海里/时 B、 $15$ 海里/时 C、 $\frac{15}{2} \sqrt{3}$ 海里/时 D、 $5 \sqrt{3}$ 海里/时

查看试题解析
5. 如图，点A到点C的距离为100米，要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上，在C点测得B在北偏东30°的方向上，则B点到河岸AD的距离为（）

A、100米 B、50米 C、 $\frac{200 \sqrt{3}}{3}$ 米 D、50 $\sqrt{3}$ 米

查看试题解析
6. 在数学课外实践活动中，小欣在河北岸AC上，在A处测得对岸的灯塔D位于南偏东 $60 °$ 方向，往东走300米到达B处，测得对岸的灯塔位于南偏东 $30 °$ 方向.则灯塔D到河北岸AC的距离约为米（结果保留根号）.

查看试题解析
7. 如图，一艘轮船以20海里/小时速度从南向北航行，当航行至A处时，测得小岛C在轮船的北偏东45度的方向处，航行一段时间后到达B处，此时测得小岛C在轮船的南偏东60度的方向处．若CB=40海里，则轮船航行的时间为．

查看试题解析
8. 如图，航母由西向东航行，到达A处时，测得小岛C位于它的北偏东60°方向，且与航母相距80海里，再航行一段时间后到达B处，测得小岛C位于它的北偏东37°方向，如果航母继续航行至小岛C的正南方向的D处，求还需航行的距离BD的长．参考数据：sin37°≈0.6，cos37°≈0.80，tan37°≈0.75

查看试题解析
9. 为了维护国家主权和海洋权力，海监部门对我国领海进行常态化巡航.如图所示，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A处测得灯塔P在北偏东60°方向上，继续航行30分钟后到达B处，此时测得灯塔P在北偏东45°方向上.

(1)、 $A B =$ 海里； $∠ A P B =$ 度；

(2)、已知在灯塔P的周围35海里内有暗礁，问海监船继续向正东方向航行是否安全？请说明理由.（参考数据： $\sqrt{2} = 1.41$ ， $\sqrt{3} = 1.73$ ）

查看试题解析
10. 我国的特高压输电技术世界领先，为了“西电东送”，需要一排排高大的自西向东电塔来支撑电线．如图，一辆汽车行驶在平行于输电线路的公路上，小明坐在车里观察 $M$ 、 $N$ 两个电塔．车在 $A$ 处时，观察到电塔 $N$ 在正北方向，车向西行驶 $100 m$ 到 $B$ 处时，观察到电塔 $M$ 在北偏东 $15 °$ ，电塔 $N$ 在北偏东 $45 °$ ．

(1)、求 $B$ 到电塔 $N$ 的距离；

(2)、求 $M$ 、 $N$ 两个电塔之间的距离．

查看试题解析

二、能力提升

11. 如图，在一笔直的沿湖道路l上有 $A$ 、 $B$ 两个游船码头，观光岛屿 $C$ 在码头 $A$ 北偏东 $60 °$ 的方向，在码头 $B$ 北偏西 $45 °$ 的方向， $A C = 4 k m$ .游客小张准备从观光岛屿 $C$ 乘船沿 $C A$ 回到码头 $A$ 或沿 $C B$ 回到码头 $B$ ，设开往码头 $A$ 、 $B$ 的游船速度分别为 $v_{1}$ 、 $v_{2}$ ，若回到 $A$ 、 $B$ 所用时间相等，则 $v_{1} ： v_{2} =$ （）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、4 D、6

查看试题解析
12. 今年贵州榕江村超爆火出圈，全国各地足球爱好者闻讯而至．在某一场足球比赛中，进攻方甲队三名球员A、C、D ，与乙队的防守球员B的位置如图所示．此时足球在球员A脚下，他想将球绕过对手B传至队友D处，再由D经线路DC回传给队友C ．已知对手B在A的北偏东60°方向，AB＝12米．球员C在对手B的正东方向，BC＝3米．球员D在队友C的正北方向，且在队友A的北偏东30°方向．（参考数据： $\sqrt{3}$ ≈1.73）

(1)、求传球线路CD的长（结果精确到1米）；

(2)、根据对手B的跑动和拦截范围估计，对手B可以破坏掉在B点5米范围内的球．球员D经线路DC传球给队友C的同时，队友C沿CD方向去接球，已知球速为10m/s ，球员C的平均速度为5m/s ．计算说明球员C是否能避开防守顺利接到球？

查看试题解析
13. 某中学组织学生进行研学活动．如图，学生到达基地大门 $A$ 处后按组分两条线路进行参观体验，最后前往宣讲中心 $B$ 处集合．经勘测， $B$ 处在 $A$ 处的正北方，手工制作区 $E$ 在 $B$ 处的南偏西 $60 °$ 方向且距离 $B$ 处400米处，农耕体验区 $D$ 在 $A$ 处的正西方，农耕体验区 $D$ 也在 $E$ 处的正南方600米处，户外拓展区 $C$ 在 $B$ 处的南偏东 $75 °$ 方向，户外拓展区 $C$ 也在 $A$ 处的北偏东 $45 °$ 方向．（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{6} \approx 2.45$ ）

(1)、求户外拓展区 $C$ 与基地大门 $A$ 之间的距离．（结果精确到 $0.1$ ）

(2)、已知第一组学生沿线路① $A - C - B$ 参观体验，在户外拓展区 $C$ 处的活动时间为40分钟，第二组学生沿线路② $A - D - E - B$ 参观体验，在农耕体验区 $D$ 处的活动时间为25分钟，在手工制作区 $E$ 处的活动时间为20分钟，若两组学生步行的平均速度均为70米/分，请通过计算说明哪一组学生先到达宣讲中心 $B$ 处．

查看试题解析
14. 金秋十一月，阳光大草坪 $A B C D$ 正处于草坪养护阶段，如图为草坪的平面示意图．经勘测，入口B在入口A的正西方向，入口C在入口B的正北方向，入口D在入口C的北偏东 $60 °$ 方向 $400 m$ 处，入口D在入口A的北偏西 $45 °$ 方向 $1000 m$ 处．（参考数据 $\sqrt{2} \approx 1.41, \sqrt{3} \approx 1.73$ ）

(1)、求 $A B$ 的长度；（结果精确到1米）

(2)、小明从入口D处进入前往M处赏花，点M在 $A B$ 上，距离入口B的 $500 m$ 处．小明可以选择鹅卵石步道① $D - C - B - M$ ，步行速度为 $50 m/min$ ，也可以选择人工步道② $D - A - M$ ，步行速度为 $60 m/min$ ，请计算说明他选择哪一条步道时间更快？（结果精确到 $0 .1min$ ）

查看试题解析

三、拓展创新

15. 小李使用握力器 $($ 如实物图所示 $)$ 锻炼手部肌肉 $.$ 如图，点 $O$ 是弹簧的上端点，调节 $A$ 处的螺旋调节器，弹簧的下端点可在 $A B$ 上的一段凹槽内移动，从而调节握力器的握力大小 $.$ 小李开始锻炼时将弹簧的下端点调到点 $C$ 处，此时弹簧的弹力是 $90 N$ ， $∠ O C B = 53 °$ ，经过一段时间的锻炼后，小李想增加锻炼强度，将弹簧下端点调至 $D$ 处，此时弹簧的弹力是 $180 N$ ， $∠ O D C = 37 °$ ，已知点 $O$ 到 $A B$ 的距离是 $4.8 c m$ ．

(1)、求 $C D$ 的长 $. ($ 结果保留一位小数 $)$

(2)、在弹性限度内，弹簧的弹力变化量与弹簧长度的变化量成正比，即 $△ F = k Δ x ($ 其中 $△ F$ 为弹簧的弹力的变化量， $k$ 为弹簧的劲度系数，单位为 $N / c m$ ， $Δ x$ 为弹簧长度的变化量 $) .$ 求该弹簧的劲度系数 $k$ ． $($ 参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75)$

查看试题解析