解直角三角形的实际应用（2）仰角俯角问题—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，已知在矩形AMNC中， $A M = 1$ 米，要测量旗杆的高度DN，运用解直角三角形的知识，只要增加以下哪些量就可以测量旗杆的高度（）

A、 $∠ α ， ∠ β$ 的大小 B、AB，BC的长度 C、 $∠ α$ 的大小和AB的长度 D、 $∠ α ， ∠ β$ 的大小和AB的长度

查看试题解析
2. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°，则船离灯塔的水平距离是（）

A、42 $\sqrt{3}$ 米 B、14 $\sqrt{3}$ 米 C、21米 D、42米

查看试题解析
3. 如图，某校教学楼 $A B$ 与 $C D$ 的水平间距 $B D = a m$ ，在教学楼 $C D$ 的顶部 $C$ 点测得教学楼 $A B$ 的顶部 $A$ 点的仰角为 $α$ ，测得教学楼 $A B$ 的底部 $B$ 点的俯角为 $β$ ，则教学楼 $A B$ 的高度是（）

A、 $(a t a n α + a t a n β) m$ B、 $(\frac{a}{t a n α} + \frac{a}{t a n β}) m$ C、 $(a s i n α + a s i n β) m$ D、 $(a c o s α + a c o s β) m$

查看试题解析
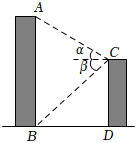4. 如图，小王在高台上的点A处测得塔底点C的俯角为α，塔顶点D的仰角为β，已知塔的水平距离AB＝a，则此时塔高CD的长为（）

A、asinα+asin β B、atanα+atan β C、 $\frac{a}{t a n a + t a n β}$ D、 $\frac{a t a n a t a n β}{t a n β}$

查看试题解析
5. 如图，一枚运载火箭从地面L处发射，雷达站R与发射点L之间的距离为6千米，当火箭到达A点时，雷达站测得仰角为 $α$ ，则这枚火箭此时的高度 $A L$ 为（）

A、 $6 s i n a$ 千米 B、 $6 c o s α$ 千米 C、 $6 t a n α$ 千米 D、 $\frac{6}{t a n α}$ 千米

查看试题解析
6. 某人在高为15米的建筑物顶部测得地面一观察点的俯角为 $60 °$ ，那么这个观察点到建筑物的距离为．

查看试题解析
7. 如图，我校数学兴趣小组在 $A$ 处用仪器测得一宣传气球顶部 $E$ 处的仰角为 $26.56 6^{°}$ ，仪器与气球的水平距离BC为30米，且距地面高度AB为2.5米，则气球顶部都离地面的高度EC是米（结果精确到0.1米， $s i n 26.56 6^{°} \approx 0.4472, c o s 26.56 6^{°} \approx 0.8944, t a n 26.56 6^{°} \approx 0.5000$ ）.

查看试题解析
8. 如图，某无人机爱好者在可飞行区域放飞无人机，当无人机飞行到一定高度 $A$ 点处时，无人机测得操控者 $B$ 的俯角约为 $53 °$ ，测得某建筑物 $C D$ 顶端点 $C$ 处的俯角约为 $45 °$ .已知操控者 $B$ 和建筑物 $C D$ 之间的水平距离为 $40 m$ ，此时无人机距地面 $B C$ 的高度为 $32 m$ ， $A$ ， $B$ ， $C$ ， $D$ 在同一平面内，求建筑物 $C D$ 的高度（计算结果保留整数）.
（参考数据： $s i n 53 ° \approx 0.799$ ， $c o s 53 ° \approx 0.602$ ， $t a n 53 ° \approx 1.33$ ）

查看试题解析

二、能力提升

9. 衢州儿童公园有摩天轮，水上乐园等娱乐设施，其中的摩天轮半径为20米，水上乐园的最高处到地面的距离为32米；如图，当摩天轮的座舱A旋转至与水上乐园最高处高度相同时，地面某观测点P与座舱A，摩天轮圆心O恰好在同一条直线上，此时测得 $∠ A P C = 30 °$ ，则 $P C$ 的距离为米；此时另一座舱B位于摩天轮最低点，摩天轮旋转一周要12分钟，若摩天轮继续逆时针旋转一周，当从座舱A观测座舱B的俯角为45°时，经过了分钟.

查看试题解析
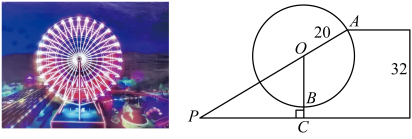10. 无人机在实际生活中的应用越来越广泛．如图所示，某人利用无人机测量某大楼的高度 $B C$ ，无人机在空中点P处，测得地面点A处的俯角为 $60 °$ ，且点P到点A的距离为 $80$ 米，同时测得楼顶点C处的俯角为 $30 °$ ．已知点A与大楼的距离 $A B$ 为70米（点A，B，C，P在同一平面内），则大楼的高度 $B C$ 为（）

A、51米 B、 $29 \sqrt{3}$ 米 C、 $30 \sqrt{3}$ 米 D、 $(40 \sqrt{3} - 10)$ 米

查看试题解析
11. 如图，某居民楼地处北半球某地，窗户朝南，窗户 $A B$ 高为1.5米， $B C D$ 表示直角遮阳棚，墙 $B C$ 长度为0.5米，此地一年的正午时刻，太阳光与地面的最大夹角为 $α$ ，测得 $t a n α = \frac{5}{3}$ ，要使太阳光刚好不射入室内，遮阳棚水平宽 $C D$ 应设计为米．

查看试题解析
12. 数学实践小组要测量某路段上一处无标识的车辆限高杆 $M N$ 的高度 $A B$ ，如图，他们先用测倾器在C处测得点A的仰角 $∠ A E G = 30 °$ ，然后在距离C处2米的D处测得点A的仰角 $∠ A F G = 45 °$ ，已知测倾器的高度为1.6米，C、D、B在水平直线上，则车辆限高杆的高度为米.
（ $\sqrt{3} \approx 1.73$ ，结果保留两位小数）

查看试题解析
13. 如图，在河流两边有甲、乙两座山，现在从甲山 $A$ 处的位置向乙山 $B$ 处拉电线.已知甲山上 $A$ 点到河边 $C$ 的距离 $A C = 130$ 米，点 $A$ 到 $C D$ 的垂直高度为120米；乙山 $B D$ 的坡比为 $4 ： 3$ ，乙山上 $B$ 点到河边 $D$ 的距离 $B D = 450$ 米，从 $B$ 处看 $A$ 处的俯角为25°（参考值： $s i n 25 ° \approx 0.423$ ， $c o s 25 ° \approx 0.906$ ， $t a n 25 ° \approx 0.466$ ）

(1)、求乙山 $B$ 处到河边 $C D$ 的垂直距离；

(2)、求河 $C D$ 的宽度.（结果保留整数）

查看试题解析

三、拓展创新

14. 仁皇阁是一个著名景点，某校九年级研学期间参观了仁皇阁，数学兴趣小组对仁皇阁高度产生了浓厚的兴趣，他们想运用所学知识估算出仁皇阁的高度。

课题	估算仁皇阁高度
测量工具	测量角度的仪器，皮尺，刻度尺等
组别	测量方案示意图	测量方案说明
组1		如图1 ，先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° ，然后从C处向阁楼底部前进10m到达D处，此时在D处测得阁楼顶端A的仰角为30° ．
组2	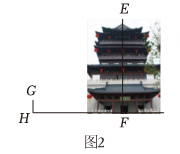	如图2 ，身高1.5m的组员站在仁皇阁正门边上合影．打印出照片后量得此组员图上高度GH为0.5cm，量得仁皇阁图上高度EF为12.9cm.

(1)、任务一请分别计算两组中测量得到的阁楼高度；（结果保留小数点后一位．参考数据

s i n 27 ° \approx 0 ． 45 ， c o s 27 ° \approx 0 ． 89 ， t a n 27 ° \approx 0 ． 50 ， \sqrt{2} \approx 1 ． 41 ， \sqrt{3} \approx 1 ． 73

）

(2)、任务二后续经过查证后发现小组2数据更为精确，请你帮小组1分析可能产生误差的原因．（写出一条即可）

查看试题解析