三角函数之间的关系—浙教版数学九(下)知识点训练
试卷更新日期:2024-12-01 类型:复习试卷
一、基础夯实
-
1. 在△ABC中,∠C=90°,如果tanA= , 那么sinB的值等于( )A、 B、 C、 D、2. 在△ABC中,∠C=90°,sinA= , 则cosB的值为( )
A、1 B、 C、 D、3. 在直角ΔABC中,已知∠C=90°, ,求cosA=( )A、 B、 C、 D、4. 下列等式成立的是( )A、. B、. C、. D、.5. 如果α是锐角,且cosα= , 那么sinα的值是( )A、 B、 C、 D、6. 已知是锐角, , 则的值为( )A、30° B、60° C、45° D、无法确定7. 已知α为锐角,且sinα= , 那么α的余弦值为( )A、 B、 C、 D、8. 在Rt△ABC中,∠C=90°,sinB= , 则tanA的值为( )A、 B、 C、 D、9. 已知α是锐角且tanα= , 则sinα+cosα=10. 在中, , 已知 , 那么的值是 .11. 若 为锐角,且 ,则 °.12. 计算:(1)、sin260°﹣tan30°•cos30°+tan45°(2)、cos245°+sin245°+sin254°+cos254°13. 已知:等腰三角形ABC中,AB=AC , ∠A是锐角,且tanA=.(1)、求sinA;(2)、若BC= , 求AB的长.14. 小明在某次作业中得到如下结果:sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=( )2+( )2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
二、能力提升
-
15. 以下说法正确的是( )A、存在锐角 ,使得sin²+cos² >1 B、已知∠A为Rt△ABC的一个内角,且∠A<45°,则sinA<cosA C、在Rt△ABC中,∠C=90°,∠A,∠B为Rt△ABC的两个内角,则sinA不一定等于cosB D、存在锐角 ,使得sin ≥tan16. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则sin∠DMN为( )
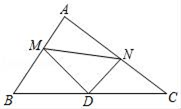 A、 B、 C、 D、17. 如图是以的边为直径的半圆 , 点恰好在半圆上,过作于 . 已知 , 则的长为 .
A、 B、 C、 D、17. 如图是以的边为直径的半圆 , 点恰好在半圆上,过作于 . 已知 , 则的长为 .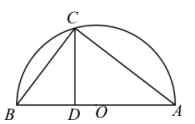 18. 如图,在△ABC中,∠ACB= ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
18. 如图,在△ABC中,∠ACB= ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5. (1)、求 的值;
(1)、求 的值;
(2)、当 时,求 的长.三、拓展创新