锐角三角函数—浙教版数学九（下）知识点训练

试卷更新日期：2024-12-01 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 在 $△ A B C$ 中， $∠ C = 9 0^{°}, A C = 12, B C = 5$ ，则 $s i n B$ 的值等于( )

A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{5}{12}$ D、 $\frac{12}{5}$

查看试题解析
2. 在 $△ A B C$ 中， $A B = 5$ ， $A C = 4$ ， $B C = 3$ ，那么 $s i n A$ 等于（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{3}$

查看试题解析
3. 如图，PA为 $⊙ O$ 的切线， $A$ 为切点.若 $P A = 3, O A = 4$ ，则 $c o s ∠ A P O$ 的值为（）

A、 $\frac{3}{4}$ . B、 $\frac{3}{5}$ . C、 $\frac{4}{5}$ . D、 $\frac{4}{3}$ .

查看试题解析
4. 在 $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ， $∠ B = 3 5^{∘}$ ， $A B = 7$ ，则 $B C$ 的长为（）

A、 $7 s i n 3 5^{∘}$ B、 $7 c o s 3 5^{∘}$ C、 $7 t a n 3 5^{∘}$ D、 $\frac{7}{c o s 3 5^{∘}}$

查看试题解析
5. 在Rt△ABC中，∠C=90°，如果把Rt△ABC的各边的长都缩小为原来的 $\frac{1}{4}$ ，则∠A的正切值（　　）

A、缩小为原来的 $\frac{1}{4}$ B、扩大为原来的4倍 C、缩小为原来的 $\frac{1}{2}$ D、没有变化

查看试题解析
6. 若0°＜α＜90°，则下列说法不正确的是（　　）

A、sinα随α的增大而增大 B、cosα随α的减小而减小 C、tanα随α的增大而增大 D、0＜sinα＜1

查看试题解析
7. 已知 $α$ 为锐角，且 $2 s i n (α - 1 0^{°}) = \sqrt{3}$ ，则 $α$ 等于（）

A、 $5 0^{°}$ B、 $6 0^{°}$ C、 $7 0^{°}$ D、 $8 0^{°}$

查看试题解析
8. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，若斜边 $A B$ 是直角边 $B C$ 的 $3$ 倍，则 $t a n B$ 的值是．

查看试题解析
9. 如图， $△ A B C$ 在正方形网格纸中，点A，B，C在格点上，则 $s i n α =$ ， $c o s α =$ ， $t a n α =$ .

查看试题解析
10. 求下列各式的值：

(1)、 $s i n 45 ° c o s 45 ° + 4 t a n 30 ° s i n 60 °$ ；

(2)、 $c o s 60 ° - 2 s i n^{2} 45 ° + \frac{2}{3} {t a n}^{2} 60 ° - s i n 30 °$ ．

查看试题解析
11. 计算：

(1)、 $\frac{1}{2} c o s 6 0^{°} + \frac{\sqrt{3}}{2} s i n 6 0^{°}$ .

(2)、 $\frac{s i n 6 0^{°}}{t a n 4 5^{°} - c o s 6 0^{°}}$ .

查看试题解析
12. 图①、图②均是6×6的正方形网格，每个小正方形的顶点称为格点.线段AB的端点均在格点上，按下列要求画出图形.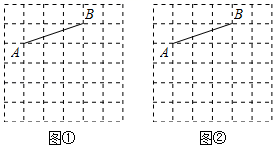

（ 1 ）在图①中找到两个格点C，使∠BAC是锐角，且tan∠BAC＝ $\frac{1}{3}$ ；

（ 2 ）在图②中找到两个格点D，使∠ADB是锐角，且tan∠ADB＝1.

查看试题解析

二、能力提升

13. 如图，直径为 $10$ 的 $⊙ A$ 上经过点 $C (0,5)$ 和点 $O (0,0)$ ， $B$ 是 $y$ 轴右侧 $⊙ A$ 优弧上一点，则 $∠ O B C$ 的余弦值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{4}{5}$

查看试题解析
14. 正方形 $A B C D$ 对角线交于O，点E和F分别在 $B C$ 和 $C D$ 延长线上，且 $B E = D F$ ，连结 $A E ， A F ， E F$ ，其中 $E F$ 与 $A C$ 和 $B D$ 交于点G和M， $G E = M G$ ，则 $tan ∠ E A C =$ （）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
15. $△ A B C$ 的两个锐角 $∠ A$ 和 $∠ B$ 满足 $| s i n A - \frac{1}{2} | + {(t a n B - 1)}^{2} = 0$ ，则 $∠ C$ 的度数是．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D，E，F分别为 $A B$ ， $A C$ 的中点，G为边 $B C$ 上一点， $∠ E G B = ∠ F D C$ ，连结 $E F$ ．若 $\tan B = \frac{4}{5}$ ， $\tan C = 2$ ， $B C = 14$ ，则 $G D$ 的长为．

查看试题解析
17. 如图1， $C D$ 是 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为点E，连接 $C A$ ．连接 $B O$ 并延长交 $⊙ O$ 于点G， $B G$ 交 $A C$ 于点F，连接 $A G$ ．

(1)、求证： $A G = 2 O E$ ；

(2)、若 $tan ∠ C A E = 2 ， A E = 1$ ，求 $A G$ 的长；

(3)、如图2，若 $A E = 1$ ，设 $tan ∠ C A E = x$ ， $\frac{G F}{B F} = y$ ．
①用含有x的代数式表示 $O B$ 的长；
②求y关于x的函数关系式．

查看试题解析
18. $△ A B C$ 和 $△ A D E$ 均是等腰直角三角形，其中 $∠ A C B = ∠ A E D = 90 °$ 如图1．开始时， $D E ∥ A C$ ，现在固定 $△ A B C$ 将 $△ A D E$ 绕着点 $A$ 按顺时针方向旋转 $α$ （ $0 < α < 180 °$ ）；

(1)、当 $△ A D E$ 中的 $D E$ 边旋转到与 $△ A B C$ 的某条边平行时，旋转角 $α$ 的度数是；

(2)、如图2，连接 $B D$ ， $C E$ ，求证： $△ A B D ∽ △ A C E$ ；

(3)、若 $A B = 2 A D$ ，在 $△ A D E$ 的旋转过程中，当 $C$ ， $D$ ， $E$ 三点在同一条直线上时，求 $∠ D B C$ 的度数．

查看试题解析
19. 如图

(1)、【基础巩固】如图1， $△ A B C$ 和 $△ A D E$ 都是等边三形，点B、D、E在同条直线上， $A C$ 与 $B E$ 交于点F.求证： $△ A D F ∽ △ C E F$ .

(2)、【尝试应用】
如图2，在（1）的条件下，若 $E F = 2 D F = 4$ ，求 $C F$ 的长度.

(3)、【拓展提高】
如图3，在平行四边形ABCD中， $∠ B A G = ∠ E A D = ∠ E D A = 60 °$ ， $B E = 3$ ， $F D = 2$ ，求 $t a n ∠ B A E$ 的值.

查看试题解析

三、拓展创新

20. 在解决代数问题时我们常会通过构建几何图形来分析.比如在计算tan15°时，如图，在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，得∠D＝15°，所以tan15° $= \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．类比这种方法，可得tan22.5°的值为（）

A、 $\sqrt{2} + 1$ B、 $\sqrt{2} - 1$ . C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
21. 魏晋时期，伟大数学家刘徽利用如图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理.已知四边形ABCD、四边形AHFE、四边形DGME均为正方形.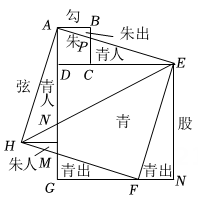

(1)、若AH=13，DE=12，则 $A B =$ ；

(2)、若 $S_{△ A B P} ： S_{△ C E P} = 1 ： 9$ ，则 $t a n ∠ D E H =$ .

查看试题解析
22. 阅读材料：关于三角函数有如下的公式：sin（α+β）＝sinαcosβ+cosαsinβ，tan（α+β） $= \frac{tan α + tan β}{1 - tan α tan β}$ .利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和（差），如tan75°＝tan（30°+45°） $= \frac{tan 45 ° + tan 30 °}{1 - tan 45 ° + tan 30 °} = \frac{1 + \frac{\sqrt{3}}{3}}{1 - 1 \times \frac{\sqrt{3}}{3}} = \frac{3 + \sqrt{3}}{3 - \sqrt{3}} =$ 2 $+ \sqrt{3}$ .
问题解决：根据以上阅读材料，请选择适当的公式解答下列问题

(1)、求sin75°；

(2)、如图，边长为2的正 $△$ ABC沿直线滚动设当 $△$ ABC滚动240°时，C点的位置在 $C^{'}$ ，当 $△$ ABC滚动480°时，A点的位置在 $A^{'}$ .
①求tan∠ $C A C^{'}$ 的值；

②试确定 $∠ C A C^{'} + ∠ C A A^{'}$ 的度数.

查看试题解析