广东省深圳市龙华区新华中学教育集团2024-2025学年上学期八年级期中考试数学试卷
试卷更新日期:2024-11-25 类型:期中考试
一、选择题:本大题共8小题,每小题3分,共24分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. ( )A、81 B、3 C、±3 D、- 32. 一直角三角形的两直角边长为6和8,则斜边长为 ( )A、8 B、9 C、10 D、113. 已知正比例函数y= kx(k≠0)的图象经过点(2,-6),则此正比例函数的关系式为( )A、 B、 C、y=3x D、y=-3x4. 下列运算正确的是 ( )A、 B、 C、 D、5. 老师写出第三象限的一点的坐标(-3,☆),小明不小心,把纵坐标给弄脏看不清了,则☆挡住的纵坐标可能是 ( )A、- 1 B、0 C、1 D、26. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
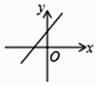 A、
A、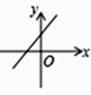 B、
B、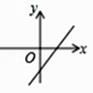 C、
C、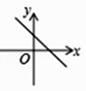 D、
D、 7. 如图,大长方形的长为x,在左侧截掉一个面积最大的正方形. 若剩余部分的周长是y,则y与x的函数关系式是 ( )
7. 如图,大长方形的长为x,在左侧截掉一个面积最大的正方形. 若剩余部分的周长是y,则y与x的函数关系式是 ( ) A、y=2x B、y=2x-2 C、y=2x+2 D、y=4x8. 如图, 在边长为5的正方形ABCD内作∠EAF=45°, AE交BC于点 E, AF交CD 于点F, 连接EF, 若DF=2, 则BE的长为( )
A、y=2x B、y=2x-2 C、y=2x+2 D、y=4x8. 如图, 在边长为5的正方形ABCD内作∠EAF=45°, AE交BC于点 E, AF交CD 于点F, 连接EF, 若DF=2, 则BE的长为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
9. 已知点P(a,b)与点Q(5,-3)关于x轴对称, 则a+b=.10. 若点A(2,y1)和点 B(-5,y2)都在直线y=-x+5上,则y1y2(选填“>”“=”或“<”).11. 如图, 在一次“寻宝”游戏中, 寻宝人找到了两个标志点A(-2,-1), C(2,-2), 则“宝藏”点 B 的坐标是.
 12. 如图所示,正方形的边长为1,则数轴上的点 P表示的实数为.
12. 如图所示,正方形的边长为1,则数轴上的点 P表示的实数为. 13. 平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y= kx+b经过点C(2,1),且恰好将△ABO平均分成面积相等的两个部分,则k的值是.
13. 平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y= kx+b经过点C(2,1),且恰好将△ABO平均分成面积相等的两个部分,则k的值是.三、解答题:本大题共7小题,共61分.
-
14. 计算下列各题:(1)、(2)、(3)、15. 已知平面直角坐标系如图所示:
 (1)、画出函数 的图象;(2)、 写一条关于这个函数图象的性质;(3)、 将 的图象向下平移1个单位,得到的函数表达式是.16. 城市绿化是城市重要的基础设施,是改善生态环境和提高广大人民群众生活质量的公益事业.某小区在社区管理人员及社区居民的共同努力之下,在临街清理出了一块可以绿化的空地(图中阴影部分).如图,点D在 中,
(1)、画出函数 的图象;(2)、 写一条关于这个函数图象的性质;(3)、 将 的图象向下平移1个单位,得到的函数表达式是.16. 城市绿化是城市重要的基础设施,是改善生态环境和提高广大人民群众生活质量的公益事业.某小区在社区管理人员及社区居民的共同努力之下,在临街清理出了一块可以绿化的空地(图中阴影部分).如图,点D在 中, (1)、 求 BC的长;(2)、 求图中阴影部分的面积.17. 如图所示的网格是由30个边长为1的小正方形组成,点A,B,C都落在格点上.
(1)、 求 BC的长;(2)、 求图中阴影部分的面积.17. 如图所示的网格是由30个边长为1的小正方形组成,点A,B,C都落在格点上. (1)、 求 的周长.(2)、求 的度数.18. 在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?
(1)、 求 的周长.(2)、求 的度数.18. 在《整式乘除》中学习了完全平方公式,还记得它是如何被发现的吗?把图①看作一个大正方形,它的面积是( 如果把图①看作是由2 个长方形和2个小正方形组成的,它的面积为 由此得到:
 (1)、【类比探究】如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是. (用a, b, c表示, 结果化为最简)(2)、【联系运用】如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当 时, 求a+b的值.(3)、【问题解决】如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH. 若该图形的周长为80, OA=12. 求该图形的面积.19. 如图,在平面直角坐标系中,已知A(a,0), B(b,0),其中a,b满足 点 M为第三象限内的一点.
(1)、【类比探究】如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图②的面积进行计算,你发现的式子是. (用a, b, c表示, 结果化为最简)(2)、【联系运用】如图②,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和一个小正方形组成的,当 时, 求a+b的值.(3)、【问题解决】如图③,将四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH. 若该图形的周长为80, OA=12. 求该图形的面积.19. 如图,在平面直角坐标系中,已知A(a,0), B(b,0),其中a,b满足 点 M为第三象限内的一点. (1)、 直接写出A,B两点的坐标;(2)、 若点 M(-2,m), 请用含 m的式子表示△ABM的面积(3)、若点.M(2-m,2m-10)到坐标轴的距离相等,且 , 求点N的坐标.20. 【项目式学习】在圆柱表面,蚂蚁怎么爬行路径最短? (π取3)
(1)、 直接写出A,B两点的坐标;(2)、 若点 M(-2,m), 请用含 m的式子表示△ABM的面积(3)、若点.M(2-m,2m-10)到坐标轴的距离相等,且 , 求点N的坐标.20. 【项目式学习】在圆柱表面,蚂蚁怎么爬行路径最短? (π取3)素材1:如图1,圆柱体的高AC为12cm,底面直径BC为6cm,在圆柱下底圆周上的A点有一只蚂蚁,它想吃到上底面圆周上与A 点对应的B 点处的食物.
若蚂蚁沿图1中的折线A→C→B爬行的最短路径记为“路线一”,此时最短路程是 12+6=18cm. 将圆柱沿着AC将侧面展开得到图2,请在图2中画出蚂蚁爬行的最短路径记为“路线二”,此时最短路程是____ cm; 比较可知:蚂蚁爬行的最短路径是路线____(用“一”或“二”填空).


素材2:如图3所示的实践活动器材包括:底面直径为6cm,高为10cm的圆柱、橡皮筋、细线(借助细线来反映爬行的路线)、直尺,通过调节橡皮筋的位置达到改变圆柱的高度的目的.
(1)、 两种路线路程的长度如表所示(单位:cm):圆柱高度
沿路线一路程x
沿路线二路程y
比较x与y的大小
5
11
x>y
4
10
x>y
3
a
3
b
(2)、填空:表格中a的值是;表格中b表示的大小关系是;(3)、经历上述探究后,请你思考:若圆柱的半径为r,圆柱的高为h. 在r不变的情况下,当圆柱半径为r与圆柱的高度h存在怎样的数量关系时,蚂蚁在圆柱表面的两种爬行路线的路程相等?