二次函数的动态几何问题—浙教版数学九(上)知识点训练
试卷更新日期:2024-11-23 类型:复习试卷
一、选择题
-
1. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
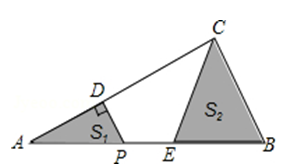 A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小2.
A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小2.如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )
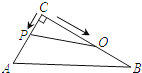 A、
A、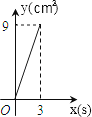 B、
B、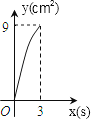 C、
C、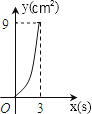 D、
D、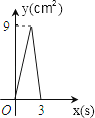 3. 如图,在△ABC中,∠B=90°,∠C=30°,AB=6cm , 动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以 cm/s的速度移动,设△BPQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )
3. 如图,在△ABC中,∠B=90°,∠C=30°,AB=6cm , 动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以 cm/s的速度移动,设△BPQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )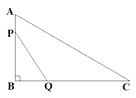 A、
A、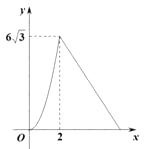 B、
B、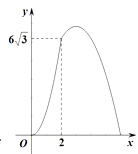 C、
C、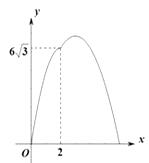 D、
D、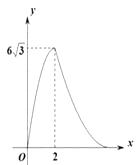 4. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
4. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图, △ABC 和 △DEF 都是边长为 2 的等边三角形,它们的边 BC,EF 在同一条直线l 上,点C,E 重合.现将 △ABC 沿直线l 向右移动,直至点 B 与 F 重合时停止移动.在此过程中,设点C 移动的距离为 x ,两个三角形重叠部分的面积为 y ,则 y 随 x 变化的函数图象大致为( )
5. 如图, △ABC 和 △DEF 都是边长为 2 的等边三角形,它们的边 BC,EF 在同一条直线l 上,点C,E 重合.现将 △ABC 沿直线l 向右移动,直至点 B 与 F 重合时停止移动.在此过程中,设点C 移动的距离为 x ,两个三角形重叠部分的面积为 y ,则 y 随 x 变化的函数图象大致为( )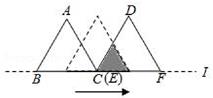 A、
A、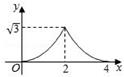 B、
B、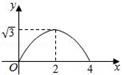 C、
C、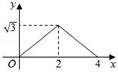 D、
D、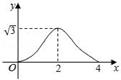 6. 如图,正方形ABCD的边长为2cm,动点 P,Q 同时从点A 出发,在正方形的边上,分别按 , 的方向,都以 1cm/s 的速度运动,到达点C运动终止,连接 PQ ,设运动时间为 x(s) ,△APQ的面积为 y(cm²) ,则下列图象中能大致表示y与x的函数关系的是( )
6. 如图,正方形ABCD的边长为2cm,动点 P,Q 同时从点A 出发,在正方形的边上,分别按 , 的方向,都以 1cm/s 的速度运动,到达点C运动终止,连接 PQ ,设运动时间为 x(s) ,△APQ的面积为 y(cm²) ,则下列图象中能大致表示y与x的函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在中, , , 于点点从点出发,沿的路径运动,运动到点停止,过点作于点 , 作于点设点运动的路程为 , 四边形的面积为 , 则能反映与之间函数关系的图象是( )
7. 如图,在中, , , 于点点从点出发,沿的路径运动,运动到点停止,过点作于点 , 作于点设点运动的路程为 , 四边形的面积为 , 则能反映与之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )
8. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )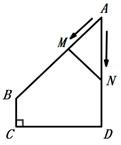 A、
A、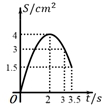 B、
B、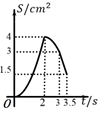 C、
C、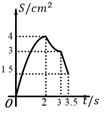 D、
D、
二、填空题
-
9. 如图,已知⊙P的半径是1,圆心P在抛物线上运动,当⊙P与x轴相切时,圆心P的坐标为 .
 10. 如图抛物线与轴交于 , 与轴交于点 , 点为顶点,线段上有一动点 , 以为底边向下作等腰三角形 , 且 , 则的最小值为 .
10. 如图抛物线与轴交于 , 与轴交于点 , 点为顶点,线段上有一动点 , 以为底边向下作等腰三角形 , 且 , 则的最小值为 . 11. 正方形的边长为6,点在边上,且 , 是边上一动点,连接 , 过点作交边于点 , 设的长为 , 则线段长度的最大值为.12. 如图,在平面直角坐标系中,二次函数 y=x2﹣2x+c 的图象与 x 轴交于 A、C 两点,与 y轴交于点 B(0,﹣3),若 P 是 x 轴上一动点,点 D(0,1)在 y 轴上,连接 PD,则 C 点的坐标是 , PD+PC 的最小值是 .
11. 正方形的边长为6,点在边上,且 , 是边上一动点,连接 , 过点作交边于点 , 设的长为 , 则线段长度的最大值为.12. 如图,在平面直角坐标系中,二次函数 y=x2﹣2x+c 的图象与 x 轴交于 A、C 两点,与 y轴交于点 B(0,﹣3),若 P 是 x 轴上一动点,点 D(0,1)在 y 轴上,连接 PD,则 C 点的坐标是 , PD+PC 的最小值是 .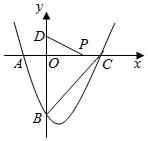
三、解答题
-
13. 二次函数y=ax2+bx+3的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C , 顶点为E .
 (1)、求点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP , 取OP中点Q , 连接QC , QE , CE , 当△CEQ的面积为12时,求点P的坐标.14. 如图,已知抛物线过点 , 且它的对称轴为.
(1)、求点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP , 取OP中点Q , 连接QC , QE , CE , 当△CEQ的面积为12时,求点P的坐标.14. 如图,已知抛物线过点 , 且它的对称轴为. (1)、求此抛物线的解析式;(2)、若点B是抛物线对称轴上的一点,且点B在第一象限,当△OAB的面积为15时,求B的坐标;(3)、是抛物线上的动点,当的值最大时,求的坐标以及的最大值.15. 如图1,一块矩形电子屏ABCD中,G为BC上一感应点,GC=2 , 动点P为一光点,当光点在光带上运动时,会与感应点发生反应,照亮以GP为边的正方形区域GPEF.因发生故障,只有光带CM和MB正常工作,CM=4,光点P以每秒1个单位的速度从C点出发,沿C→M→B匀速运动,到达点B时停止.设光点P的运动时间为t秒,照亮的正方形区域GPEF的面积为S.图2为P点在运动过程中S与t的函数图象,其中点Q表示P点运动到B点时情形.
(1)、求此抛物线的解析式;(2)、若点B是抛物线对称轴上的一点,且点B在第一象限,当△OAB的面积为15时,求B的坐标;(3)、是抛物线上的动点,当的值最大时,求的坐标以及的最大值.15. 如图1,一块矩形电子屏ABCD中,G为BC上一感应点,GC=2 , 动点P为一光点,当光点在光带上运动时,会与感应点发生反应,照亮以GP为边的正方形区域GPEF.因发生故障,只有光带CM和MB正常工作,CM=4,光点P以每秒1个单位的速度从C点出发,沿C→M→B匀速运动,到达点B时停止.设光点P的运动时间为t秒,照亮的正方形区域GPEF的面积为S.图2为P点在运动过程中S与t的函数图象,其中点Q表示P点运动到B点时情形. (1)、图2中a=;当t=1时,照亮的区域面积S= .(2)、当点P经过M点又运动4秒时,照亮区域的面积达到了最小,已知此时S是t的二次函数.求出点P在整个运动过程中S关于t的函数解析式;(3)、若存在三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等.①t1+t2=;②当t3=4t1时,则正方形GPEF的面积为 .
(1)、图2中a=;当t=1时,照亮的区域面积S= .(2)、当点P经过M点又运动4秒时,照亮区域的面积达到了最小,已知此时S是t的二次函数.求出点P在整个运动过程中S关于t的函数解析式;(3)、若存在三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等.①t1+t2=;②当t3=4t1时,则正方形GPEF的面积为 .